Цифровое моделирование пространственной фильтрации изотропных элементов изображения в форме круга
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
Министерство образования и науки Российской Федерации ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б. Н. Ельцина» Институт естественных наук и математики Лабораторная работа №2 по дисциплине «Оптические методы обработки информации» Тема: «Цифровое моделирование пространственной фильтрации изотропных элементов изображения в форме круга»
Екатеринбург 2021 Цель: изучить влияние на тестовое изображение размеров и геометрии фильтров. КРАТКАЯ ТЕОРИЯ Найдём аналитическое соотношение для амплитуды и интенсивности изображения в выходной плоскости схемы оптической пространственной фильтрации (см. рис. 1) в зависимости от пространственной координаты ρ и частоты среза фильтра β, для тестового изображения в форме круга 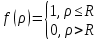 , (1) , (1)где R – радиус круга, ρ – радиус круга в полярной системе координат. При пространственной фильтрации элементов изображения f(ρ), обладающего осевой симметрией, двумерное преобразование Фурье 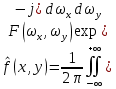 (2) (2)сводится к одномерному преобразованию Ганкеля и распределение амплитуды света в выходной плоскости 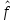 можно записать: можно записать: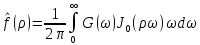 , (3) , (3)где G(ω) – пространственный спектр тестового изображения в форме круга, 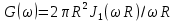 , (4) , (4)J0, J1 – функции Бесселя нулевого и первого порядков. Используя в (3) соотношение (2) и учитывая конечные размеры фильтра β в плоскости ω, получим:  . (5) . (5)При замене ωR = x и ρ/R = α соотношение (5) примет вид: 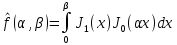 . (6) . (6)Соотношение (6) в замкнутой форме не выражается, и поэтому было рассчитано численно. Результаты численных расчётов были использованы при построении графиков зависимостей амплитуды 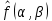 и интенсивности и интенсивности 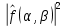 в выходной плоскости оптической схемы пространственной фильтрации элементов изображения в форме круга от пространственной координаты α и частоты среза фильтра β. в выходной плоскости оптической схемы пространственной фильтрации элементов изображения в форме круга от пространственной координаты α и частоты среза фильтра β.Для высокочастотной пространственной фильтрации амплитуду и интенсивность изображения в выходной плоскости (хвых, увых) можно найти по результатам фильтрации нижних частот: 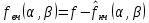 , (7) , (7)где f – исходный пространственный сигнал, fнч – распределение сигнала в выходной плоскости при фильтрации нижних пространственных частот, фильтром дополнительным к фильтру верхних пространственных частот. Графики распределения интенсивности света при высокочастотной фильтрации приведены на рисунке 3д. На рисунке 4 приведена схема оптической пространственной фильтрации осесимметричного входного тестового изображения круга диаметром 2r, ограниченного диафрагмой с диаметром 2R полосовым пространственным фильтром с частотой среза [β0н - β0в]. Для тестового элемента изображения в форме кольца: 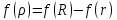 . (8) . (8)Пространственный спектр изображения, для этого случая, определяется соотношением: 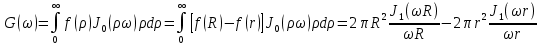 . (9) . (9)Для сигнала в выходной плоскости получим соотношение: 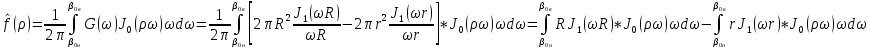 . (10) . (10)Если ввести обозначение: ωR = x, n = r/R, α = ρ/R, то получим: 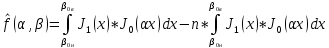 . (11) . (11)Полученные соотношения позволяют численно рассчитать распределение амплитуды  для различных вариантов пространственной фильтрации асимметричного входного сигнала ограниченного, в общем случае, диафрагмой. для различных вариантов пространственной фильтрации асимметричного входного сигнала ограниченного, в общем случае, диафрагмой.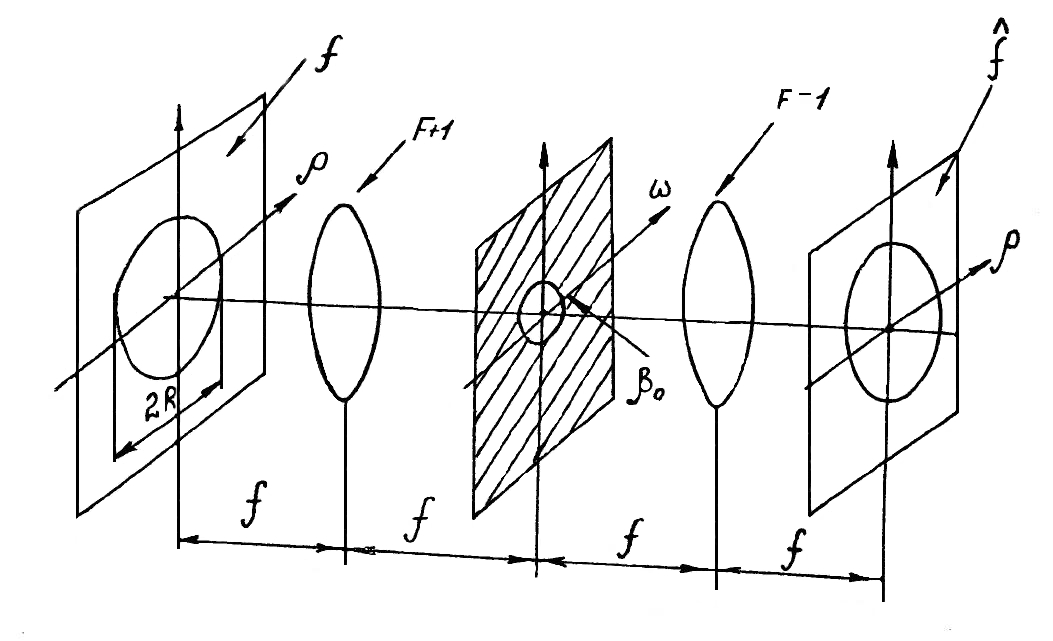 Рис.1. Схема пространственной фильтрации элементов изображения в форме круга   – плоскости входного ( – плоскости входного ( ) и обработанного ( ) и обработанного ( ) изображения; ) изображения;F+1, F-1 – условные обозначения прямого и обратного преобразования Фурье; ρ, ω – пространственная координата и частота; β0 – частота среза фильтра. 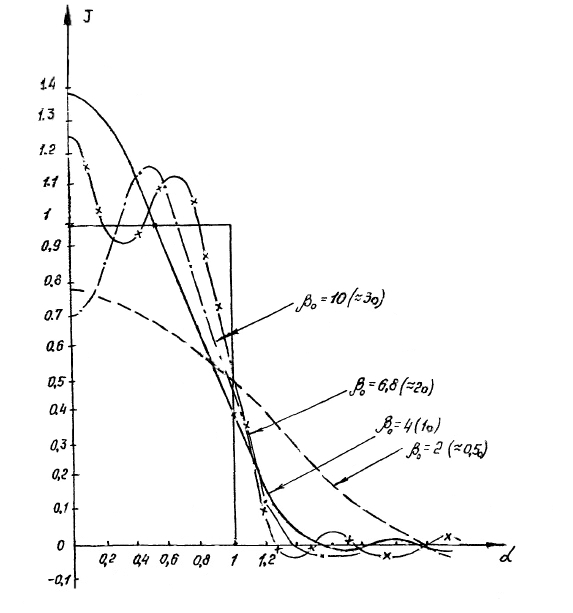 Рис.2. Распределение амплитуды света 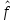 при низкочастотной фильтрации изображения круга для пространственных низкочастотных фильтров с частотой среза β0 = 2 ;4; 6; 8; 10. при низкочастотной фильтрации изображения круга для пространственных низкочастотных фильтров с частотой среза β0 = 2 ;4; 6; 8; 10.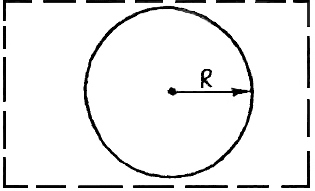 Рис.3а. Тестовое изображение в форме круга. 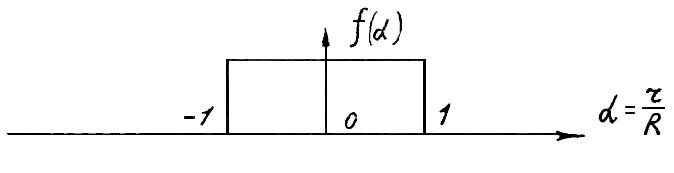 Рис.3б. Распределение амплитуды света в плоскости тестового изображения. 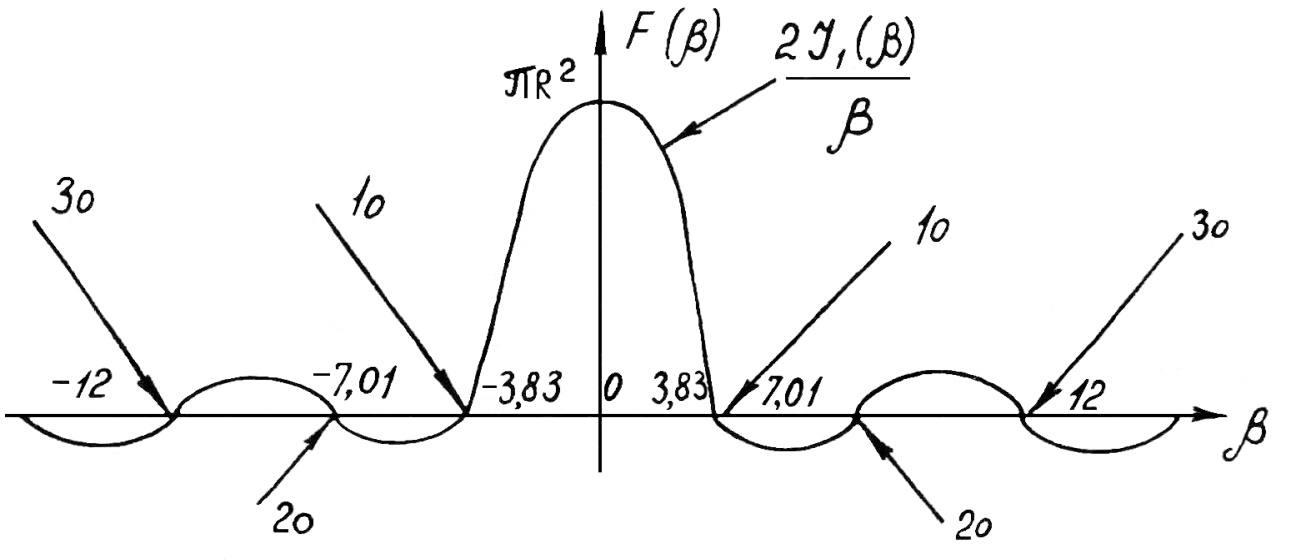 Рис.3в. Пространственный спектр тестового изображения в форме круга. 10, 20, 30 – условное обозначение положения нулей в спектре тестового сигнала. 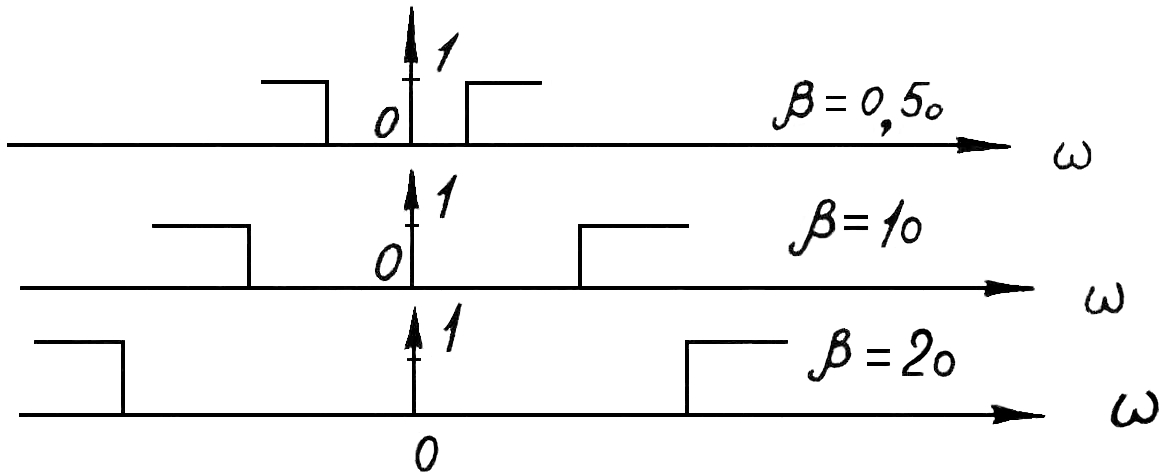 Рис.3г. Частотные характеристики высокочастотных фильтров, размещённых в плоскости пространственных частот ω (β – частота среза фильтра). 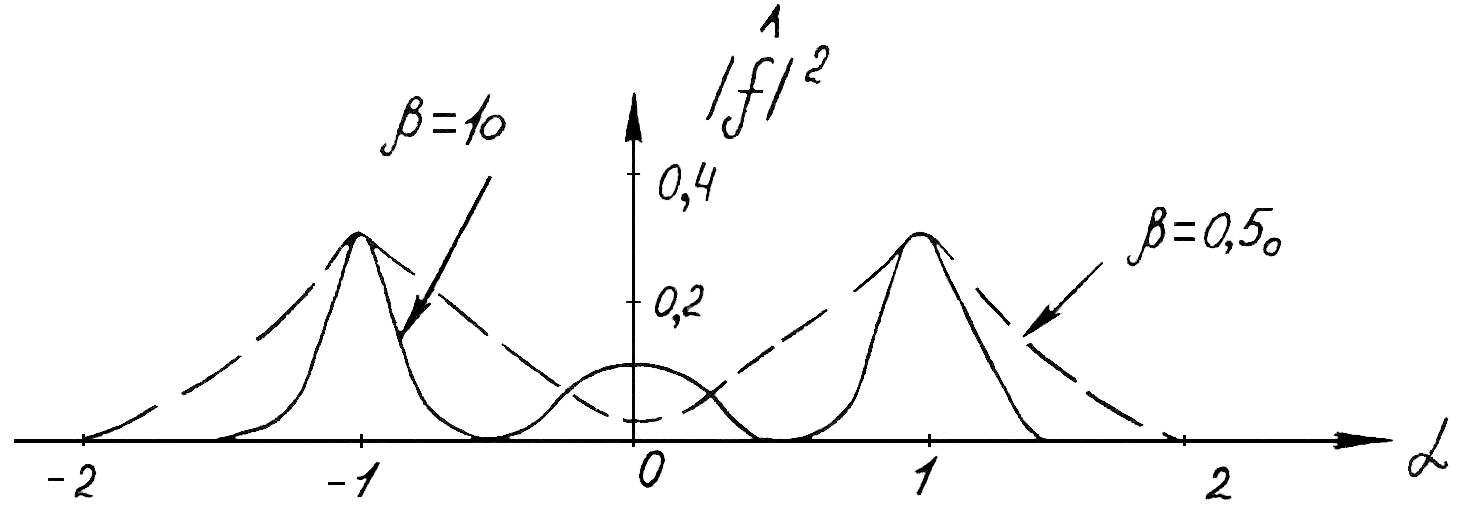 Рис. 3д. Распределение интенсивности света в плоскости обработанного изображения (круг). 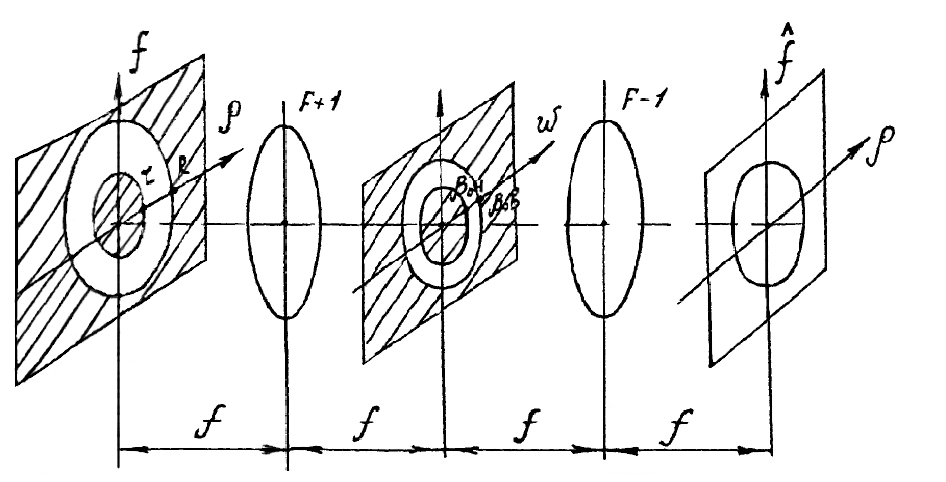 Рис. 4. Схема пространственной полосовой фильтрации элемента изображения в форме круга r, ограниченного диафрагмой R.  – плоскости входного ( – плоскости входного (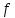 ) и обработанного ( ) и обработанного (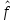 ) изображения; ) изображения;F+1, F-1 – условные обозначения прямого и обратного преобразования Фурье; ρ, ω – пространственная координата и частота; β0н, β0в – нижняя и верхняя частоты среза полосового фильтра. Отчет 1. Пространственный спектр изображения в форме круга представляет собой выражение 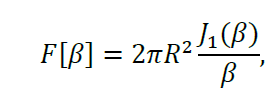 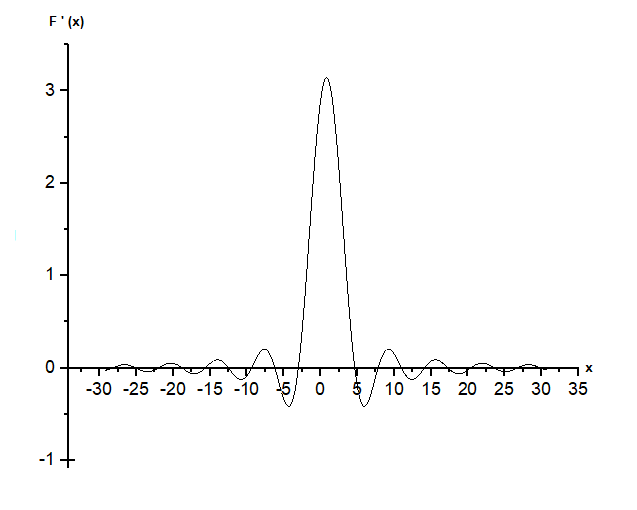 Рис. 5- Изображение пространственного спектра сигнала круглой формы 2. Фильтрация спектра была выполнена для низкочастотного фильтра с часто-тами среза 𝛽0=1;10.
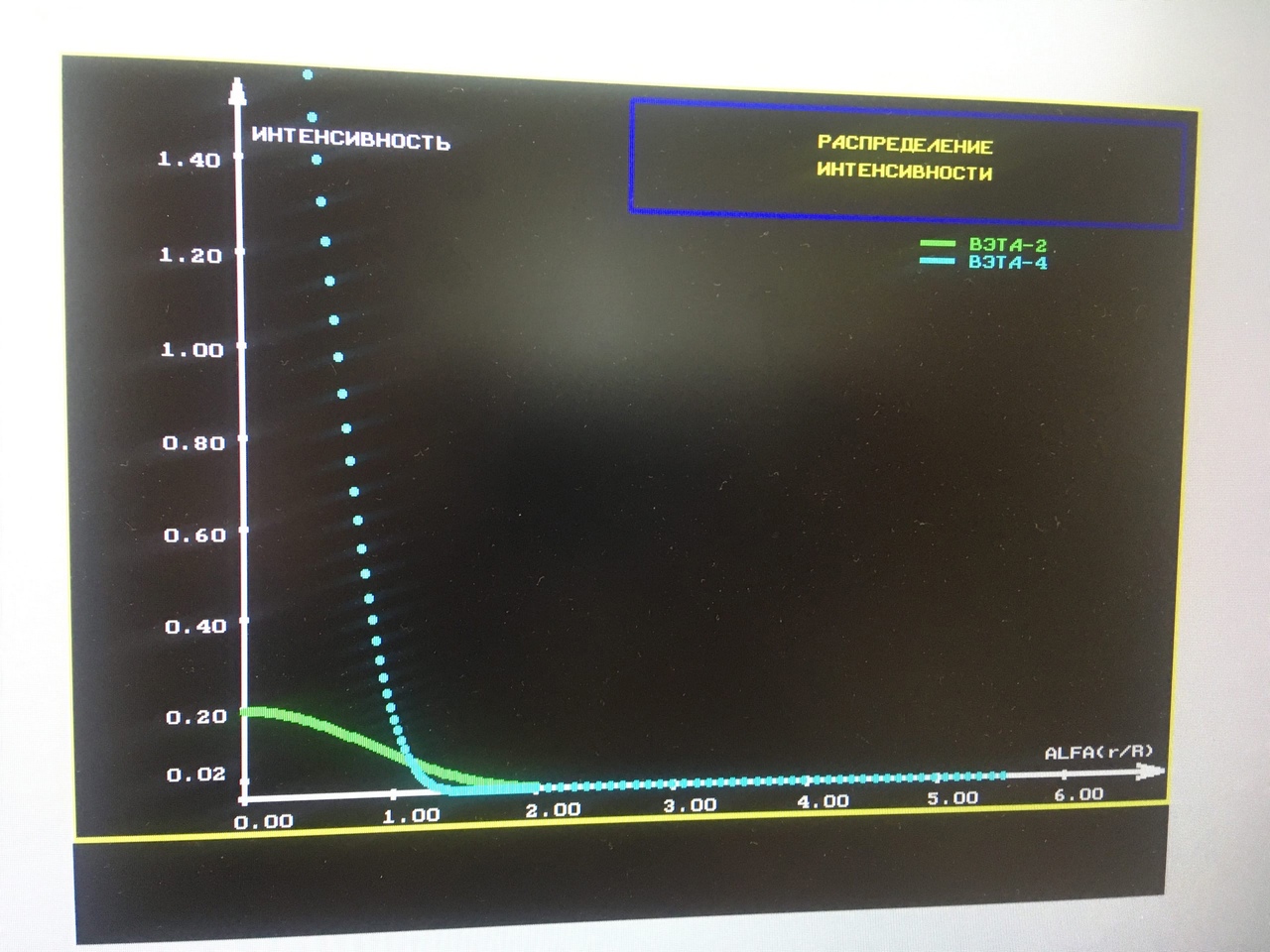 Рис. 6- Распределение интенсивности для высокочастотного фильтра 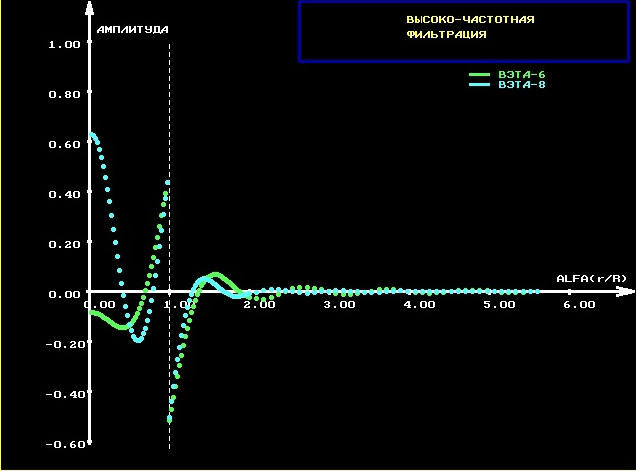 Рис. 7- Распределение амплитуды для высокогочастотного фильтра 3. Построить спектр сигнала в относительных единицах G(β) спектра изображения в форме круга (радиуса r), ограниченного диафрагмой (радиуса R) для соотношения n = r/R, приведённого в таблице. Для построения спектра необходимо воспользоваться соотношением 1: 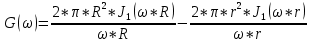 , ,при условии, что β = ω*r, а J1(ω*R) – функция Бесселя первого порядка.
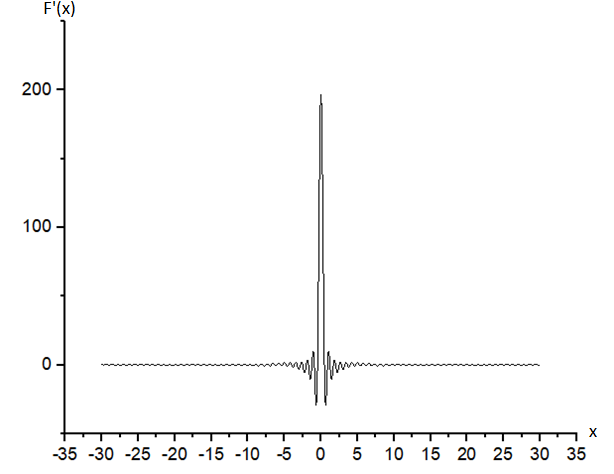 Рис. 8 – пространственный амплитудный спектр при n = 1/8 4 . Используя результаты расчёта в режиме «COUNT» и соотношение (1) из теории установить, как будет изменяться сигнал в выходной плоскости для данных, указанных в таблице.
Примечания: 10 – положение первого нуля в спектре пространственного сигнала; 40 − положение четвертого нуля в спектре пространственного сигнала; и т. д. Для расчёта можно воспользоваться способом, представленном ниже. 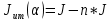 = =где J = Jв - Jн; Jит – итоговая интенсивность сигнала; Jв − интенсивность при верхней частоте среза; Jн − интенсивность при нижней частоте среза. В таблице с результатами расчёта («COUNT») в первой колонке указаны α, а во второй – интенсивность сигнала. 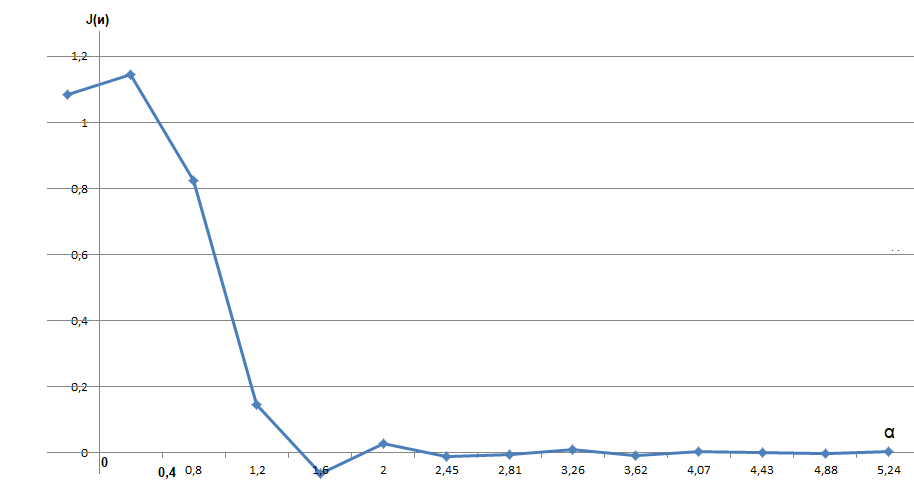 .Используя соотношение (11) определить способ пространственной фильтрации для вариантов, указанных в таблице.
случае, когда 𝑛≠0, 𝛽0Н= 𝛽, 𝛽0В= ∞, где β0Н и β0В – нижняя и верхняя частоты срезов соответственно, и учитывая соотношение (11) делаем вывод что используется фильтр высоких частот для изображения в форме круга. |
