Вентили и булева алгебра. Цифровой логический уровень
 Скачать 441.52 Kb. Скачать 441.52 Kb.
|
|
Цифровой логический уровень В самом низу иерархической схемы уровней архитектуры компьютера находится цифровой логический уровень, или аппаратное обеспечение компьютера. Здесь мы рассмотрим различные аспекты цифровой логики, что должно послужить основой для изучения более высоких уровней в дальнейшем. Вентили и булева алгебра Цифровые схемы могут конструироваться из небольшого числа простых элементов путем сочетания этих элементов в различных комбинациях. Ниже мы опишем эти основные элементы, покажем, как их можно сочетать, Вентили Цифровая схема — это схема, в которой есть только два логических значения. Обычно сигнал от 0 до 1 В представляет одно значение (например, 0), а сигнал от 2 до 5 В — другое значение (например, 1). Напряжение за пределами указанных величин недопустимо. Крошечные электронные устройства, которые называются вентилями, могут вычислять различные функции от этих двузначных сигналов. Эти вентили формируют основу аппаратного обеспечения, на которой строятся все цифровые компьютеры. Принцип работы вентилей относится к уровню физических устройств, который находится ниже уровня 0. Вся современная цифровая логика основывается на том, что транзистор может работать как очень быстрый бинарный переключатель. На рис. 3.1, а изображен биполярный транзистор, встроенный в простую схему. Транзистор имеет три соединения с внешним миром: коллектор, базу и эмиттер. Если входное напряжение УIN ниже определенного критического значения, транзистор выключается и действует как очень большое сопротивление. Это приводит к выходному сигналу VOUT, близкому к VCC (напряжению, подаваемому извне), обычно +5 В для данного типа транзистора. Если VIN превышает критическое значение, транзистор включается и действует как провод, вызывая заземление сигнала VOUT (по соглашению 0 В). 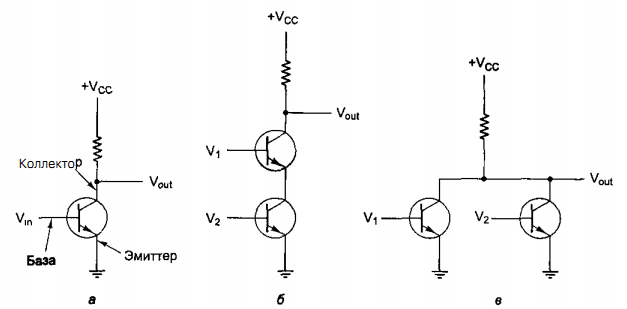 Рис. 3.1. Транзисторный инвертор (а); вентиль НЕ-И (б); вентиль НЕ-ИЛИ (в) Важно отметить, что если напряжение VIN низкое, то VOUT высокое, и наоборот. Эта схема, таким образом, является инвертором, превращающим логический 0 в логическую 1 и логическую 1 в логический 0. Резистор (ломаная линия) нужен для ограничения количество тока, проходящего через транзистор, чтобы транзистор не сгорел. На переключение с одного состояния на другое обычно требуется несколько наносекунд. На рис. 3.1, 6 два транзистора соединены последовательно. Если и напряжение V1 и напряжение V2 высокое, то оба транзистора будут служить проводниками и снижать VOUT. Если одно из входных напряжений низкое, то соответствующий транзистор будет выключаться и напряжение на выходе будет высоким. Другими словами, VOUT будет низким тогда и только тогда, когда и напряжение V1, и напряжение V2 высокое. На рис. 3.1, в, два транзистора соединены параллельно. Если один из входных сигналов высокий, будет включаться соответствующий транзистор и снижать выходной сигнал Если оба напряжения на входе низкие, то выходное напряжение будет высоким. Эти три схемы образуют три простейших вентиля. Они называются вентилями НЕ, НЕ-И и НЕ-ИЛИ. Вентили НЕ часто называют инверторами. Мы будем использовать оба термина. Если мы примем соглашение, что высокое напряжение (VСС) — это логическая 1, а низкое напряжение («земля») — логический 0, то мы сможем выражать значение на выходе как функцию от входных значений. Значки, которые используются для изображения этих трех типов вентилей, показаны на рис. 3.2, а — в. Там же приводится поведение функции для каждой схемы. На этих рисунках А и В — это входные сигналы, а X — выходной сигнал. 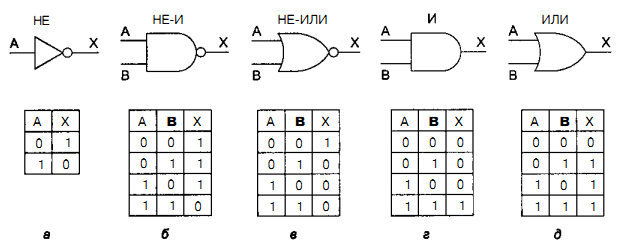 Рис. 3.2. Значки для изображения 5 основных вентилей. Поведение функции для каждого вентиля Если выходной сигнал (см. рис. 3.1, б) подать в инвертор, мы получим другую схему, противоположную вентилю НЕ-И, то есть такую схему, у которой выходной сигнал равен 1 тогда и только тогда, когда оба входных сигнала равны 1. Такая схема называется вентилем И; ее схематическое изображение и описание соответствующей функции даны на рис. 3.2, г. Точно так же вентиль НЕ-ИЛИ может быть связан с инвертором. Тогда получится схема, у которой выходной сигнал равен 1 в том случае, если хотя бы один из входных сигналов — 1, и равен 0, если оба входных сигнала равны 0. Изображение этой схемы, ко горая называется вентилем ИЛИ, а также описание соответствующей функции даны на рис. 3.2, д. Маленькие кружочки в схемах инвертора, вентиля НЕ-И и вентиля НЕ-ИЛИ называются инвертирующими выходами. Пять вентилей, изображенных на рис. 3.2, составляют основу цифрового логического уровня. Из предшествующего обсуждения должно быть ясно, что вентили НЕ-И и НЕ-ИЛИ требуют два транзистора каждый, а вентили И и ИЛИ — три транзистора каждый. По этой причине во многих компьютерах используются вентили НЕ-И и НЕ-ИЛИ, а не И и ИЛИ. Две основные технологии производства вентилей — биполярная и МОП (металл-оксид-полупроводник). Среди биполярных технологий можно назвать ТТЛ (транзисторно-транзисторную логику), которая служила основой цифровой электроники на протяжении многих лет, и ЭСЛ (эмиттерно-связанную логику), которая используется в тех случаях, когда требуется высокая скорость выполненияопераций. Вентили МОП работают медленнее, чем ТТЛ и ЭСЛ, но потребляют гораздо меньше энергии и занимают гораздо меньше места, поэтому можно компактно расположить большое количество таких вентилей. Булева алгебра Чтобы описать схемы, которые строятся путем сочетания различных вентилей, нужен особый тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1. Такая алгебра называется булевой алгеброй. На самом деле в данном случае мы говорим об особом типе булевой алгебры, а именно об алгебре релейных схем, но термин «булева алгебра» очень часто используется в значении «алгебра релейных схем». Как и в обычной алгебре (то есть в той, которую изучают в школе), в булевой алгебре есть свои функции. Булева функция имеет одну или несколько переменных и выдает результат, который зависит только от значений этих переменных. Можно определить простую функцию f, сказав, что f(A)=l, если А=0, и f(A)=-O, если А=1. Такая функция будет функцией НЕ (см. рис. 3.2, а). Так как булева функция от n переменных имеет только 2n возможных комбинаций значений переменных, то такую функцию можно полностью описать в таблице с 2n строками. В каждой строке будет даваться значение функции для разных комбинаций значений переменных. Такая таблица называется таблицей истинности. Хотя любая булева функция может быть определена с помощью таблицы истинности, с возрастанием количества переменных такой тип записи становится громоздким. Поэтому вместо таблиц истинности часто используется другой тип записи. Чтобы увидеть, каким образом осуществляется этот другой тип записи, отметим, что любую булеву функцию можно определить, указав, какие комбинации значений переменных дают значение функции 1. Мы будем рисовать черту над переменной, чтобы показать, что ее значение инвертируется. Отсутствие черты означает, что значение переменной не инвертируется. Кроме того, мы будем использовать знак умножения (точку) для обозначения булевой функции И (знак умножения может опускаться) и + для обозначения булевой функции ИЛИ. Например, для функции от трех переменных такая запись может выглядеть следующим образом: F = AB + ĀC Это компактная запись таблицы истинности. Таким образом, функцию от n переменных можно описать суммой максимум 2n произведений, при этом в каждом произведении будет по п множителей. Как мы скоро увидим, такая формулировка особенно важна, поскольку она ведет прямо к реализации данной функции с использованием стандартных вентилей. Реализация булевых функций и эквивалентность схем Реализовать схему для любой булевой функции можно используя следующие шаги: Составить таблицу истинности для данной функции. Обеспечить инверторы, чтобы порождать инверсии для каждого входного сигнала. Нарисовать вентиль И для каждой строки таблицы истинности с результатом 1. Соединить вентили И с соответствующими входными сигналами. Вывести выходы всех вентилей И в вентиль ИЛИ. Здесь показано, как реализовать любую булеву функцию с использованием вентилей НЕ, И и ИЛИ. Однако гораздо удобнее строить схемы с использованием одного типа вентилей. К счастью, можно легко преобразовать схемы, построенные по предыдущему алгоритму, в форму НЕ-И или НЕ-ИЛИ. Чтобы осуществить такое преобразование, все, что нам нужно, — это способ воплощения НЕ, И и ИЛИ с по- мощью одного типа вентилей. На рисунке 3.4 показано, как это можно сделать, используя только вентили НЕ-И или только вентили НЕ-ИЛИ. Отметим, что существуют также другие способы подобного преобразования. 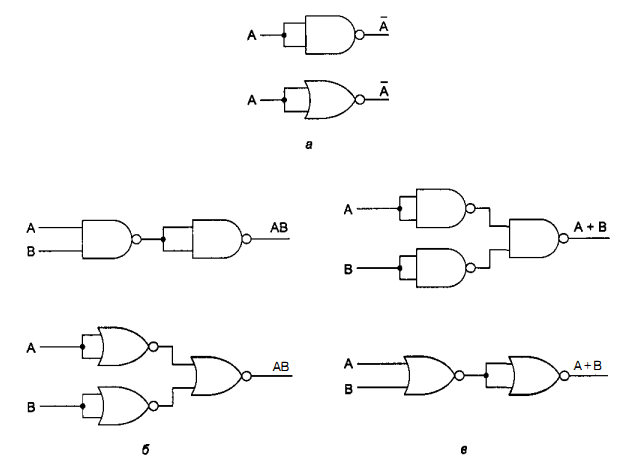 Рис. 3.4. Конструирование вентилей НЕ (а), И (б) и ИЛИ (в) с использованием только вентилей НЕ-И или только вентилей НЕ-ИЛИ Разработчики схем часто стараются сократить число вентилей, чтобы снизить цену,уменьшить занимаемое схемой место, сократить потребление энергии и т. д. Чтобы упростить схему, разработчик должен найти другую схему, которая может вычислять ту же функцию, но при этом требует меньшего количества вентилей (или может работать с более простыми вентилями, например двухвходовыми вместо четырехвходовых). Булева алгебра является ценным инструментом в поиске эквивалентных схем. Обычно разработчик исходит из определенной булевой функции, а затем применяет к ней законы булевой алгебры, чтобы найти более простую функцию, эквивалентную исходной. На основе полученной функции можно конструировать схему. Очень важно отметить, что один и тот же вентиль может вычислять разные функции в зависимости от используемых соглашений. Если мы примем соглашение, что 0 В — это логический ноль, а 3,3 В или 5 В — логическая единица, мы получим одну таблицу истинности Такое соглашение называется позитивной логикой. Однако если мы примем негативную логику, то есть условимся, что 0 В — это логическая единица, а 3,3 В или 5 В — логический ноль, то мы получим другую таблицу истинности. Основные цифровые логические схемы В предыдущих разделах мы увидели, как реализовать простейшие схемы с использованием отдельных вентилей. На практике в настоящее время схемы очень редко конструируются вентиль за вентилем, хотя когда-то это было распространено. Сейчас стандартные блоки представляют собой модули, которые содержат ряд вентилей. Далее мы рассмотрим эти стандартные блоки более подробно Интегральные схемы Вентили производятся и продаются не по отдельности, а в модулях, которые называются интегральными схемами (ИС) или микросхемами. Интегральная схема представляет собой квадратный кусочек кремния небольшого размера. Микросхемы можно разделить на несколько классов с точки зрения количе- ства вентилей, которые они содержат. Эта классификация, конечно, очень грубая, но иногда она может быть полезна: МИС (малая интегральная схема): от 1 до 10 вентилей. СИС (средняя интегральная схема): от 1 до 100 вентилей. БИС (большая интегральная схема): от 100 до 100 000 вентилей. СБИС (сверхбольшая интегральная схема): более 100 000 вентилей. Эти схемы имеют различные свойства и используются для различных целей. МИС обычно содержит от двух до шести независимых вентилей, каждый из которых может использоваться отдельно. Подобные микросхемы стоят несколько центов. Каждая микросхема МИС содержит несколько вентилей и примерно до 20 выводов. В 70-е годы компьютеры конструировались из большого числа таких микросхем, но в настоящее время на одну микросхему помещается целый центральный процессор и существенная часть памяти (кэш-памяти). Для удобства мы считаем, что у вентиля появляются изменения на выходе, как только появляются изменения на входе. На самом деле существует определенная задержка вентиля, которая включает в себя время прохождения сигнала через микросхему и время переключения. Время задержки обычно составляет от 1 до 10 нс. В настоящее время стало возможным помещать до нескольких десятков миллионов транзисторов на одну микросхему. Так как любая схема может быть сконструирована из вентилей НЕ-И, может создаться впечатление, что производитель способен изготовить микросхему, содержащую 5 млн вентилей НЕ-И. К несчастью, для создания такой микросхемы потребуется 15 000 002 выводов. Поскольку стандартный вывод занимает 0,1 дюйм, микросхема будет более 18 км в длину, что отрицательно скажется на покупательной способности. Поэтому чтобы использовать преимущество данной технологии, нужно разработать такие схемы, у которых количество вентилей сильно превышает количество выводов. Комбинационные схемы Многие применения цифровой логики требуют наличия схем с несколькими входами и несколькими выходами, в которых выходные сигналы определяются текущими входными сигналами. Такая схема называется комбинационной схемой. Не все схемы обладают таким свойством. Например, схема, содержащая элементы памяти, может генерировать выходные сигналы, которые зависят от значений, хранящихся в памяти. Микросхема, которая реализует таблицу истинности сложной функции, является типичным примером комбинационной схемы. Мультиплексоры На цифровом логическом уровне мультиплексор представляет собой схему с 2n входами, одним выходом и n линиями управления, которые выбирают один из входов. Выбранный вход соединяется с выходом. На рис. 3.10 изображена схема восьмивходового мультиплексора. Три линии управления А, В и С кодируют 3-битное число, которое указывает, какая из восьми линий входа должна соединяться с вентилем ИЛИ и, следовательно, с выходом. Вне зависимости от того, какое значение будет на линиях управления, семь вентилей И будут всегда выдавать на выходе 0, а оставшийся может выдавать или 0, или 1 в зависимости от значения выбранной линии входа. Каждый вентиль И запускается определенной комбинацией линий управления. 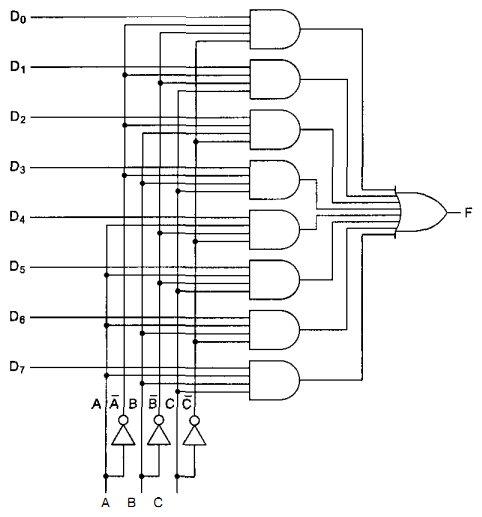 Рис. 3.10. Схема восьмивходового мультиплексора Мультиплексор может использоваться для выбора одного из нескольких входов и для реализации таблицы истинности. Его также можно использовать в качестве преобразователя параллельного кода в последоваельный. Если подать 8 битов данных на линии входа, а затем переключать линии управления последовательно от 000 до 111 (это двоичные числа), 8 битов поступят на линию выхода последовательно. Противоположностью мультиплексора является демультиплексор, который соединяет единственный входной сигнал с одним из 2n выходов в зависимости от значений n линий управления. Если бинарное значение линий управления равно к, то выбирается выход к. Декодеры В качестве второго примера рассмотрим схему, которая получает на входе n-битное число и использует его для того, чтобы выбрать (то есть установить на значение 1) одну из 2n выходных линий. Такая схема называется декодером. Пример декодера для n=3 показан на рис. 3.12. Чтобы понять, зачем нужен декодер, представим себе память, состоящую из 8 микросхем, каждая из которых содержит 1 Мбайт. Микросхема 0 имеет адреса от 0 до 1 Мбайт, микросхема 1 — адреса от 1 Мбайт до 2 Мбайт и т. д. Три старших двоичных разряда адреса используются для выбора одной из восьми микросхем.На рис. 3.12 эти три бита — три входа А, В и С В зависимости от входных сигналов ровно одна из восьми выходных линий (D0,..., D7) принимает значение 1; остальные линии принимают значение 0. Каждая выходная линия запускает одну из восьми микросхем памяти. Поскольку только одна линия принимает значение 1, запускается только одна микросхема. 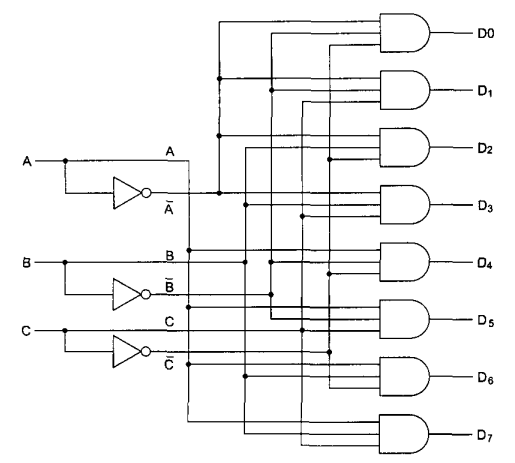 Рис. 3.12. Схема декодера, содержащего 3 входа и 8 выходов Принцип работы схемы, изображенной на рис. 3.12, не сложен. Каждый вентиль И имеет три входа, из которых первый или А, или 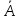 , второй или В, или , второй или В, или 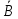 , а третий или С, или , а третий или С, или 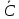 . Каждый вентиль запускается различной комбинацией входов: D0 — сочетанием . Каждый вентиль запускается различной комбинацией входов: D0 — сочетанием 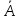 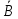 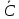 , D7 — А В С и т. д. , D7 — А В С и т. д.Компараторы Еще одна полезная схема — компаратор. Компаратор сравнивает два слова, которые поступают на вход. Компаратор, изображенный на рис. 3.13, принимает два входных сигнала, А и В, каждый длиной 4 бита, и выдает 1, если они равны, и 0, если они не равны. Схема основывается на вентиле ИСКЛЮЧАЮЩЕЕ ИЛИ, который выдает 0, если сигналы на входе равны, и 1, если сигналы на входе не равны. Если все четыре входных слова равны, все четыре вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ должны выдавать 0. Эти четыре сигнала затем поступают в вентиль ИЛИ. Если в результате получается 0, значит, слова, поступившие на вход, равны; в противном случае они не равны. В нашем примере мы использовали вентиль ИЛИ в качестве конечной стадии, чтобы поменять значение полученного результата: 1 означает равенство, а 0 — неравенство. 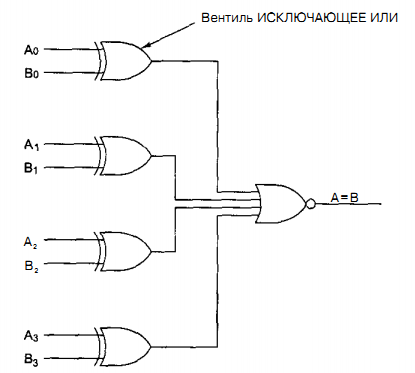 Рис. 3.13. Простой четырехразрядный компаратор Программируемые логические матрицы Ранее рассказывалось, что любую функцию (таблицу истинности) можно представить в виде суммы произведений и, следовательно, воплотить в схеме, используя вентили И и ИЛИ. Для вычисления сумм произведений служит так называемая программируемая логическая матрица (рис. 3.14). Эта микросхема содержит входы для 12 переменных. Дополнительные сигналы (инверсии) генерируются внутри самой микросхемы. В итоге всего получается 24 входных сигнала. Какой именно входной сигнал поступает в определенный вентиль И, определяется по матрице 24x50 бит. Каждая из входных линий к 50 вентилям И содержит плавкую перемычку. При выпуске с завода все 1200 перемычек остаются нетронутыми. Чтобы запрограммировать матрицу, покупатель выжигает выбранные перемычки, прикладывая к схеме высокое напряжение. 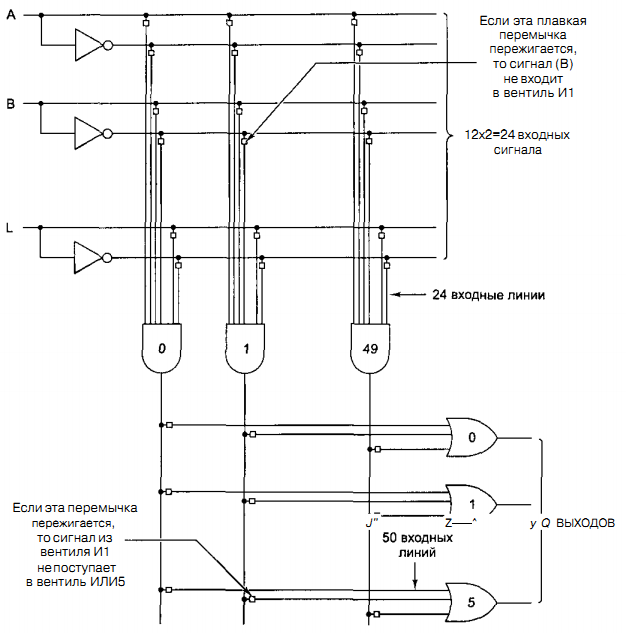 Рис. 3.14. Программируемая логическая матрица с 12 входами и 6 выходами. Маленькие квадратики — плавкие перемычки, выжигаемые для задания функции, которую нужно вычислить, Плавкие перемычки упорядочиваются в двух матрицах. Верхняя матрица — для вентилей И, а нижняя матрица — для вентилей ИЛИ Матрицы, программируемые в условиях эксплуатации, все еще используются. Однако предпочтение отдается матрицам, которые изготавливаются на заказ. Они разрабатываются заказчиком и выпускаются производителем в соответствии с запросами заказчика. Такие программируемые логические матрицы гораздо дешевле. Арифметические схемы Схемы сдвига Первой арифметической схемой СИС, которую мы рассмотрим, будет схема сдвига, содержащая 8 входов и 8 выходов (рис. 3.15). Восемь входных битов подаются на линии D0,..., D7. Выходные данные, которые представляют собой входные данные, сдвинутые на 1 бит, поступают на линии S0, ..., S7. Линия управления С определяет направление сдвига: 0 — налево, 1 — направо. 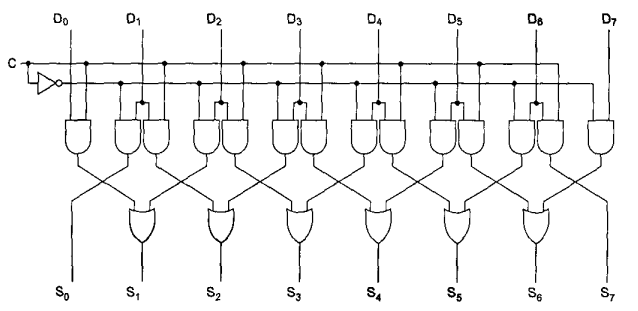 Рис. 3.15. Схема сдвига. Чтобы понять, как работает такая схема, рассмотрим пары вентилей И (кроме крайних вентилей) Если С=1, правый член каждой пары включается, пропуская через себя соответствующий бит. Так как правый вентиль И соединен с входом вентиля ИЛИ, который расположен справа от этого вентиля И, происходит сдвиг вправо. Если С=0, включается левый вентиль И из пары, и тогда происходит сдвиг влево. Сумматоры Схема для выполнения операций сложения является существенной частью любого процессора. Таблица истинности для сложения одноразрядных целых чисел показана на рис. 3.16, а. Здесь имеется два результата: сумма входных переменных А и В и перенос на следующую (левую) позицию. Схема для вычисления бита суммы и бита переноса показана на рис. 3.16,6. Такая схема обычно называется полусумматором. 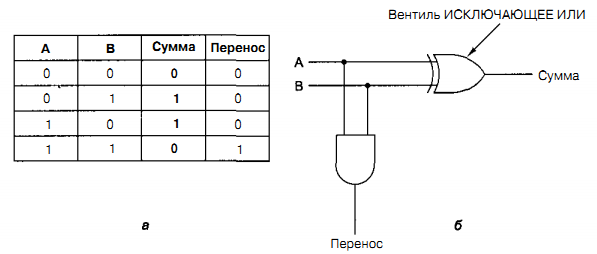 Рис. 3.16. Таблица истинности для сложения одноразрядных чисел (а); схема полусумматора (б) Полусумматор подходит для сложения битов нижних разрядов двух многобитовых слов. Но он не годится для сложения битов в середине слова, потому что не может осуществлять перенос в эту позицию. Поэтому необходим полный сумматор (рис. 3.17). Из схемы должно быть ясно, что полный сумматор состоит из двух полусумматоров. Сумма равна 1, если нечетное число переменных А, В и Вход переноса принимает значение 1 (то есть если единице равна или одна из переменных, или все три). Выход переноса принимает значение 1, если или А и В одновременно равны 1 (левый вход в вентиль ИЛИ), или если один из них равен 1, а Вход переноса также равен 1. Два полусумматора порождают и биты суммы, и биты переноса. Чтобы построить сумматор, например, для двух 16-битных слов, нужно продублировать схему, изображенную на рис. 3.17, б, 16 раз. Перенос производится в левый соседний бит. Перенос в самый правый бит соединен с 0. Такой сумматор называется сумматором со сквозным переносом. 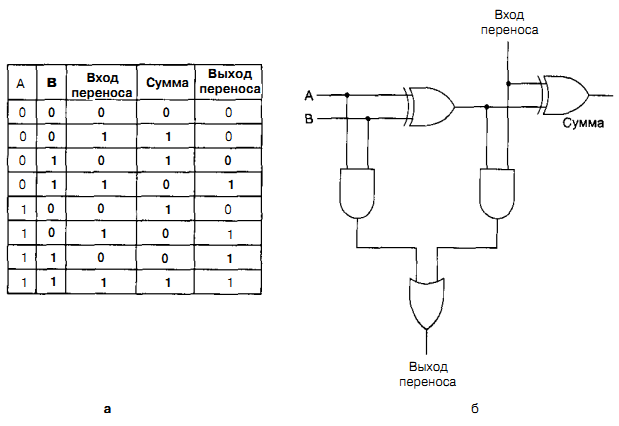 Рис.3.17. Таблица истинности для полного сумматора (а); схема для полного сумматора (б) Арифметико-логические устройства Большинство компьютеров содержат одну схему для выполнения операций И, ИЛИ и сложения над двумя машинными словами. На рис. 3.18 изображена такая схема, которая называется арифметико-логическим устройством, или АЛУ. Это устройство может вычислять одну из 4 следующих функций: А И В, А ИЛИ В, В и А+В. Выбор функции зависит от того, какие сигналы поступают на линии F0 и F1: 00,01,10 или 11 (в двоичной системе счисления)  Рис. 3.18. Одноразрядное АЛУ. В левом нижнем углу схемы находится двухразрядный декодер, который порождает сигналы включения для четырех операций. В верхнем левом углу схемы находится логическое устройство для вычисления А И В, А ИЛИ В и В, но по крайней мере один из этих результатов проходит через последний вентиль ИЛИ в зависимости от того, какую из разрешающих линий выбрал декодер. Так как ровно один из выходных сигналов декодера будет равен 1, то и запускаться будет ровно один из четырех вентилей И. Остальные три вентиля будут выдавать 0 независимо от значений А и В. В нижнем правом углу находится полный сумматор для подсчета суммы А и В и для осуществления переносов. Переносы необходимы, поскольку несколько таких схем могут быть соединены для выполнения операций над целыми словами. Одноразрядные схемы, подобные той, которая изображена на рис. 3.18, называются разрядными микропроцессорными секциями. Тактовые генераторы Во многих цифровых схемах все зависит от порядка, в котором выполняются действия. Иногда одно действие должно предшествовать другому, иногда два действия должны происходить одновременно. Для контроля временных отношений в цифровые схемы встраиваются тактовые генераторы, чтобы обеспечить синхронизацию. Тактовый генератор — это схема, которая вызывает серию импульсов. Все импульсы одинаковы по длительности. Интервалы между последовательными импульсами также одинаковы. Временной интервал между началом одного импульса и началом следующего называется временем такта. Частота импульсов обычно от 1 до 500 МГц, что соответствует времени такта от 1000 нс до 2 нс. Частота тактового генератора обычно контролируется кварцевым генератором, чтобы достичь высокой точности. В компьютере за время одного такта может произойти много событий. Если они должны осуществляться в определенном порядке, то такт следует разделить на подтакты. Чтобы достичь лучшего разрешения, чем у основного тактового генератора, нужно сделать ответвление от задающей линии тактового генератора и вставить схему с определенным временем задержки. Таким образом порождается вторичный сигнал тактового генератора, который сдвинут по фазе относительно первичного (рис 3 20, а). Временная диаграмма (рис 3 20, б) обеспечивает четыре начала отсчета времени для дискретных событии: 1 Нарастающий фронт С1 2 Задний фронт С1 3 Нарастающий фронт С2 4 Задний фронт С2 Связав различные события с различными фронтами, можно достичь требуемой последовательности выполнения действий.  Рис. 3.20. Тактовый генератор {а), временная диаграмма для тактового генератора (б), порождение асинхронных тактовых импульсов {в) |
