Cистема численно-математического моделирования MatLab. Cистема численноматематического моделирования MatLab
 Скачать 73.78 Kb. Скачать 73.78 Kb.
|
|
http://bourabai.kz/cm/matlab02.htm Cистема численно-математического моделирования MatLabМатрицы
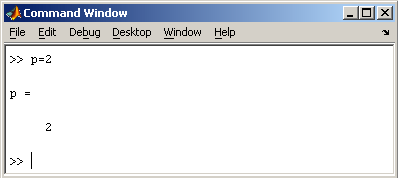 Заметим, что MatLab различает заглавные и прописные буквы, так что p и P — это разные переменные. Для ввода массивов (векторов или матриц) их элементы заключают в квадратные скобки. Так для ввода вектора-строки размером 1×3, используется следующая команда, в которой элементы строки отделяются пробелами или запятыми. 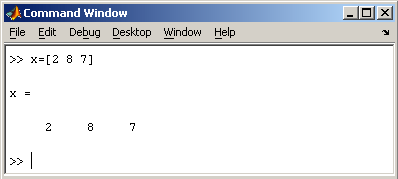 При вводе вектора-столбца элементы разделяют точкой с запятой. Например, 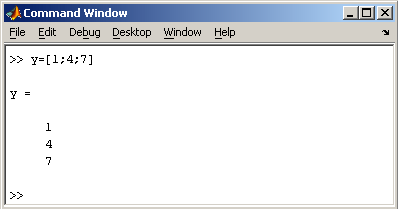 Вводить небольшие по размеру матрицы удобно прямо из командной строки. При вводе матрицу можно рассматривать как вектор-столбец, каждый элемент которого является вектором-строкой. 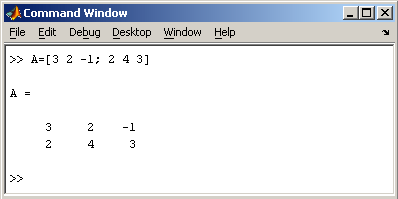 или матрицу можно трактовать как вектор строку, каждый элемент которой является вектором-столбцом. 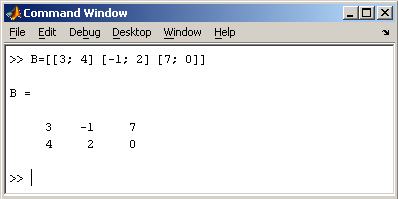 Доступ к элементамДоступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например команда B(2,3) выдаст элемент второй строки и третьего столбца матрицы B. Для выделения из матрицы столбца или строки следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием. Например, запишем вторую строку матрицы A в вектор z 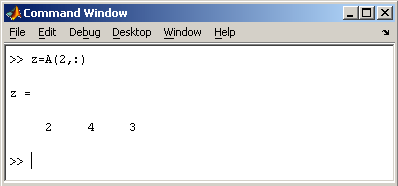 Также можно осуществлять выделение блоков матриц при помощи двоеточия. Например, выделим из матрицы P блок отмеченный цветом 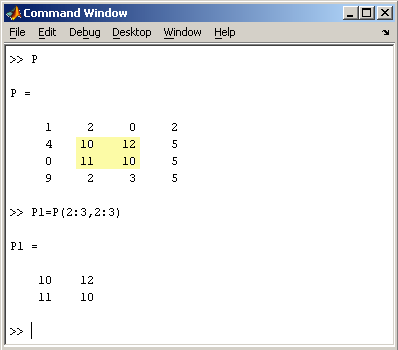 Если необходимо посмотреть переменные рабочей среды, в командной строке необходимо набрать команду whos. 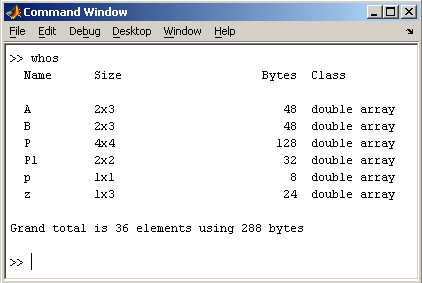 Видно, что в рабочей среде содержатся один скаляр (p), четыре матрицы (A, B, P, P1) и вектор-строка (z). Основные матричные операцииПри использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус 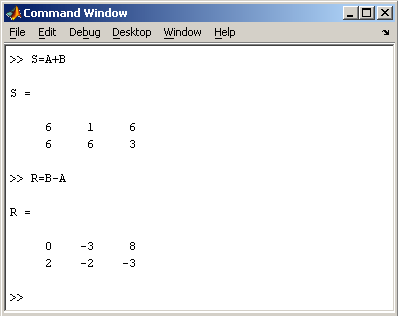 а умножение — знаком звездочка *. Введем матрицу размером 3×2 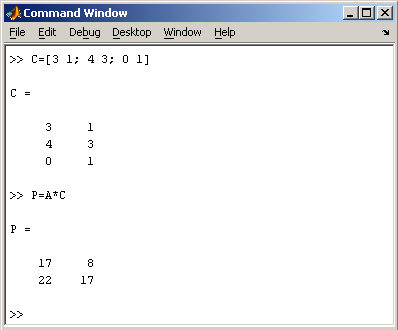 Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^ 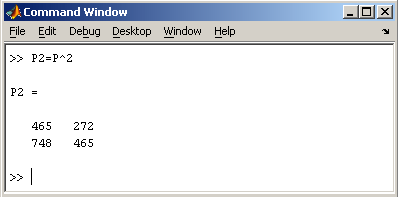 Проверьте полученный результат, умножив матрицу Р саму на себя. Создание матриц специального видаЗаполнение прямоугольной матрицы нулями производится встроенной функцией zeros 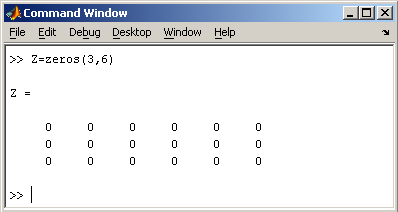 Единичная матрица создается при помощи функции eye 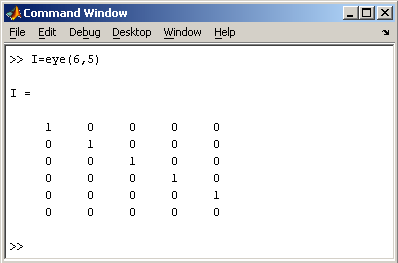 Матрица, состоящая из единиц, образуется в результате вызова функции ones 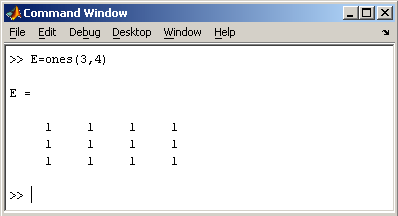 MatLab предоставляет возможность заполнения матриц случайными числами. Результатом функции rand является матрица чисел, равномерно распределенных между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону с нулевым средним и единичной дисперсией. Функция diag формирует диагональную матрицу из вектора, располагая элементы по диагонали. Матричные вычисленияMatLab содержит множество различных функций для работы с матрицами. Так, например, транспонирование матрицы производится при помощи апострофа ' 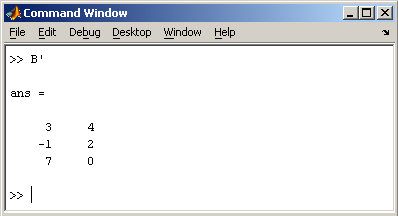 Нахождение обратной матрицы проводится с помощью функции inv для квадратных матриц 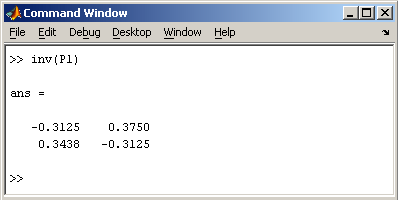 Псевдообратную матрицу можно найти с помощью функции pinv. Более подробно про обработку матричных данных можно узнать, если вывести список всех встроенных функций обработки данных командой help datafun, а затем посмотреть информацию о нужной функции, например help max. |
