Бесконечно длинный провод. Бесконечно длинный провод с током I. D 20 cм 0,2 м
 Скачать 0.64 Mb.
|
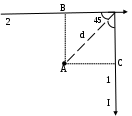
На основании принципа суперпозиции индукцию магнитного поля в точке А можно представить как сумму индукций полей, создаваемых участками проводника 1 и 2: В = В1 + В2  Зная направление тока в проводнике по правилу винта определим направление векторов В1 и В2. для этого будем винт вращать так, чтобы он поступательно двигался по направлению тока в проводнике. Тогда сторона винта, обращенная к точке А, будет перемещаться к наблюдателю перпендикулярно плоскости рисунка. Это указывает направление вектора индукции. Применяя это правило к участкам проводника 1 и 2, найдем, что векторы индукции В1 и В2 направлены к нам. Тогда В = В1 + В2. Применение закона Био-Савара-Лапласа для определения индукции магнитного поля отрезка прямолинейного проводника приводит к формуле: 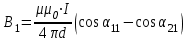 где: 11 = 0; 21 = 45.Индукция магнитного поля, создаваемая вторым проводником: 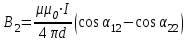 где: 12 = 135; 22 = .Найдем индукцию магнитного поля в точке А: 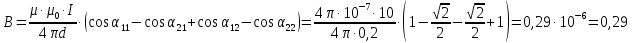 мкТл Проверка размерности: 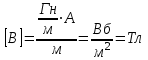 Ответ: 0,29 мкТл ЭДС батареи равна 20 В. Сопротивление R внешней цепи равно 2 Ом, сила тока I = 4 А. Найти КПД батареи. При каком значении внешнего сопротивления R КПД будет равен 99%? Решение: КПД батареи: η=UE100η=UE100%, где U=IRU=IR - падение напряжения на внешнем сопротивлении. То есть: η=IRE100η=IRE100% η=4⋅220100=40η=4⋅220100=40% η1=U1E,U1=η1Eη1=U1E,U1=η1E (здесь КПД в долях единицы), U1=I1R1⇒I1R1=η−1E,R1=η1EI1U1=I1R1⇒I1R1=η−1E,R1=η1EI1 (1) I1=Er+R1⇒r+R1=EI1I1=Er+R1⇒r+R1=EI1 (2) (2) разделим на (1): r+R1R1=EI1I1η1Er+R1R1=EI1I1η1E. rR1+1=1η1,rR1=1η1−1,rR1=1−η1η1rR1+1=1η1,rR1=1η1−1,rR1=1−η1η1, R1r=η11−η1,R1=η11−η1rR1r=η11−η1,R1=η11−η1r (3) E=IR+Ir,Ir=E−IR,r=E−IRIE=IR+Ir,Ir=E−IR,r=E−IRI (4) (4)→(3):R1=η11−η1E−IRI,R1=0,991−0,9920−4⋅24=297Ом(4)→(3):R1=η11−η1E−IRI,R1=0,991−0,9920−4⋅24=297Ом. Ответ: η = 40%; R = 297 Ом  |