контрольная. ЗАДАЧА 2. Данное выражение представим в виде

• Название: Данное выражение представим в виде
• Анкор: контрольная
• Дата: 27.03.2022
• Размер: 303.16 Kb.
• Имя файла: ЗАДАЧА 2.docx
• Тип: Документы; #420693

ЗАДАНИЕ 2. Определение устойчивости системы согласно критериям Михайлова и Найквиста Пользуясь критериями устойчивости Михайлова и Найквиста определить устойчивость одноконтурной системы управления, имеющую в разомкнутом состоянии передаточную функцию вида



Построить годографы Михайлова и Найквиста. Определить частоту среза системы. Определить критическое значение коэффициента усиления системы. Исходные данные берутся из табл. 1.1. Решите задачу с использованием MicrosoftExcel.

Таблица 1.1. Значения параметров системы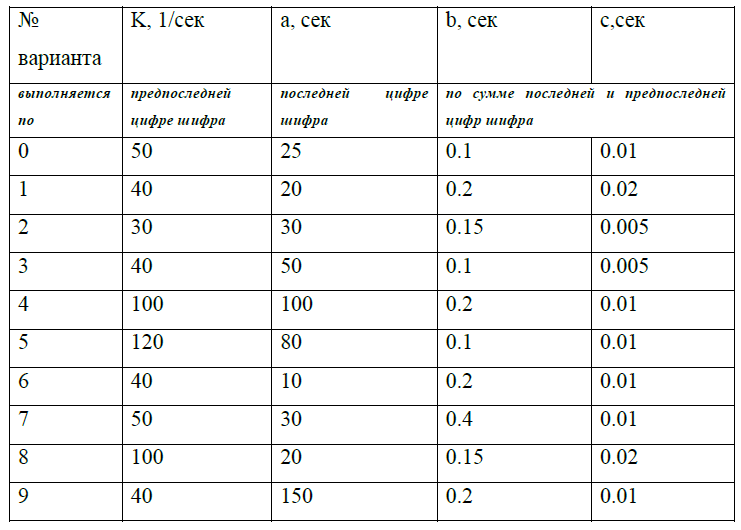



Для оценки устойчивости по критерию Михайлова необходимо построить кривую, которую описывает конец вектора на комплексной плоскости при изменении частоты от 0 до , называемую годографом Михайлова.

Вектор получают из характеристического полинома замкнутой системы при подстановке

(1)

Данное выражение представим в виде

, (2)
где и , – вещественная и мнимая части соответственно

. (3)

Подставляя численные значения, получим

. (4)

Задавая значения от 0 до , вычисляем и . Расчет оформляем в виде таблицы 1.

Таблица 1 – Координаты годографа Михайлова

ω	0	5	10	15	20	25	30	35	40	45	50	∞
Х(ω)	36,1	-0,226875	-96,63	-215,37688	-293,58	-243,19688	48,97	721,27312	1937,22	3885,4731	6779,85	∞
Y(ω)	0	-2,20625	-47,65	-179,56875	-441,2	-875,78125	-1526,55	-2436,7438	-3649,6	-5208,356	-7156,25	∞

По данным таблицы 1 строим годограф Михайлова (рисунок 1).

Исследование системы на устойчивость по критерию Найквиста

Определим устойчивость разомкнутой системы.

В одноконтурной системе, составленной из последовательно соединенных звеньев, корни характеристических полиномов этих звеньев являются одновременно корнями характеристического полинома разомкнутой системы. Так как система не содержит местных обратных связей, определим корни характеристических полиномов звеньев.

Характеристический полином звена

(5)

имеет вещественный корень

= -16,67

Характеристический полином звена

(6)
имеет три корня, один из которых нулевой:

р₂= 0; р₃= ‒ 2,33; р₄= ‒ 15,38.

Так как один корень имеет нулевое значение, разомкнутая система находится на границе устойчивости.

Передаточная функция разомкнутой системы имеет вид

(7)

Составим частотную передаточную функцию

, (8)

где ;

;

;

.
Запишем вещественную и мнимую части частотной передаточной функции

. (9)

Подсчитаем значения мнимой и действительной части частотной передаточной функции для различных значений от 0 до . Результаты вычислений оформим в виде таблицы 2.

Таблица 2 – Расчет АФЧХ разомкнутой системы

ω	U1	V1	U2	V2	U(ω)	V(ω)
0,1	36,1	0	-0,0149498	0,09994235	-52,848657	-353,30289
1	36,1	0	-1,493323	0,94235	-17,28939	-10,910337
2	36,1	0	-5,953168	1,5388	-5,6842127	-1,4692793
3	36,1	0	-13,319163	1,44345	-2,6789169	-0,2903247
4	36,1	0	-23,490688	0,3104	-1,5365109	-0,0203031
5	36,1	0	-36,326875	-2,20625	-0,9901026	0,06013217
6	36,1	0	-51,646608	-6,4524	-0,6882387	0,08598419
7	36,1	0	-69,228523	-12,77395	-0,5042917	0,0930512
8	36,1	0	-88,811008	-21,5168	-0,3839445	0,09302063
9	36,1	0	-110,0922	-33,02685	-0,3008333	0,09024777
10	36,1	0	-132,73	-47,65	-0,2409296	0,08649359
20	36,1	0	-329,68	-441,2	-0,0392339	0,0525054
30	36,1	0	12,87	-1526,55	0,00019936	0,02364641
40	36,1	0	1901,12	-3649,6	0,00405286	0,00778031
50	36,1	0	6743,75	-7156,25	0,00251783	0,00267184
60	36,1	0	16351,92	-12392,4	0,00140229	0,00106274
70	36,1	0	32939,27	-19703,95	0,00080714	0,00048282
80	36,1	0	59121,92	-29436,8	0,0004893	0,00024362
90	36,1	0	97918,47	-41936,85	0,00031153	0,00013342
∞	36,1	0	∞	∞	0	0

По данным таблицы 2 построим график АФЧХ разомкнутой системы.

Определение устойчивости системы по логарифмическим частотным характеристикам

Запишем передаточную функцию разомкнутой системы в виде

, (10)
где общий коэффициент передачи системы К=К₁К₂К₃К₄=36,1

Определим частоты сопряжения по формуле

, (11)

где , постоянная времени i-го звена.

Тогда, применив формулу для нахождения частот, получим

(12)

Так как данная система содержит интегрирующее звено, то она является нейтральной. Рассчитаем ординату для низкочастотной асимптоты для звена согласно формуле до первой частоты сопряжения:

(13)

При построении ЛАЧХ звену будет соответствовать наклон , а звену наклон будет равен , звену будет соответствовать наклон , звену будет соответствовать наклон

Рассчитаем параметры для построения ЛФЧХ разомкнутой системы, путем суммирования ЛФЧХ всех звеньев. Значения углов вычисляются в диапазоне частот от минимальной частоты, соответствующей началу координат до частоты, при которой фазовый сдвиг превышает (–180^º).

Для звена ЛФЧХ будет вычисляться по формуле:

(14)

Для звеньев :

(15)

Значения результирующей ЛФЧХ найдем как:

(16)

Подставив численные значения в вышеприведенные формулы, рассчитаем необходимые значения. Результаты вычислений оформим
в виде таблицы 3.

Результаты вычислений отобразим на графике логарифмических характеристик разомкнутой системы (рисунок3).

Таблица 3 – Расчет ЛФЧХ разомкнутой системы

частота	Звено 1		Звено 2		Звено 3		Звено 4		ΣΦ(ω)
	ωТ1	Φ1(ω)	ωТ2	Φ2(ω)	ωТ3	Φ3(ω)	ωТ4	Φ4(ω)
0,01		-1,570796	0,0043	-0,0043	0,00065	-0,00065	0,0006	-0,0006	-90,31799
0,1		-1,570796	0,043	-0,0429735	0,0065	-0,0064999	0,006	-0,0059999	-93,17839
1		-1,570796	0,43	-0,4060981	0,065	-0,0649087	0,06	-0,0599282	-120,42033
2,33		-1,570796	1,0019	-0,7863473	0,15145	-0,1503077	0,1398	-0,1388998	-151,62475
10		-1,570796	4,3	-1,3422997	0,65	-0,5763752	0,6	-0,5404195	-230,89573
15,38		-1,570796	6,6134	-1,420725	0,9997	-0,7852481	0,9228	-0,7452699	-259,09377
16,67		-1,570796	7,1681	-1,432184	1,08355	-0,8254765	1,0002	-0,7854982	-264,36015
100		-1,570796	43	-1,5475447	6,5	-1,418147	6	-1,4056476	-340,4593

Рисунок 3 – Логарифмические частотные характеристики разомкнутой системы

Если разомкнутая система нейтральна, для ее устойчивости в замкнутом состоянии, необходимо и достаточно, чтобы число переходов ЛФЧХ через линию –180° при положительных значениях ЛАЧХ было четным (в частном случае равным нулю).

В данном случае ЛФЧХ совершает один отрицательный переход при положительных значениях ЛАЧХ. Можно сделать вывод о том, что замкнутая система неустойчива.