Расчетная часть. Пример. Освоение методов анализа линейных электрических цепей постоянного тока. ДЗ 1-1э. Дано e 1 100 B E
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Вариант 4. Дано: E1 = 100 B; E2 = E4 = 50 B; E3 = 80 B. R1 = 80 Ом; R2 = 50 Ом; R3 = 40 Ом; R4 = 30 Ом; R5 = R7 = 20 Ом; R6 = 30 Ом. Е = 40 В. Ветвь R3; заменить R1 → (E). 1. Схема согласно заданному варианту. 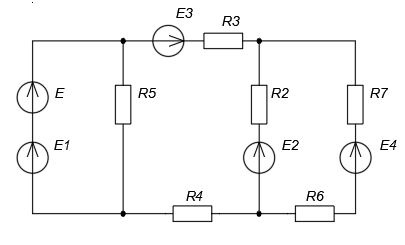 Схема 1. 2. Количество узлов q = 4, ветвей – p = 6 (схема 2). 3. Составление уравнений по законам Кирхгофа. Число уравнений по первому закону Кирхгофа: (q-1) = (4-1) = 3; по второму – (p-q+1) = (6-4+1) = 3. Обозначим узлы a,b,c,d и пронумеруем контуры 1,2,3.  Схема 2. Уравнения: узел a I1 – I3 – I5 = 0; узел b I3 – I7 – I2 = 0; узел с I7 + I2 – I4 = 0; контур 1 R5·I5 = E1 + E; контур 2 R3·I3 + R2·I2 + R4·I4 - R5·I5 = E3 - E2; контур 3 (R7+R6) ·I7 - R2·I2 = E2 – E4. 4.1. Расчет методом узловых токов. Обозначим токи в контурах через Il, ImиIn (схема 3). 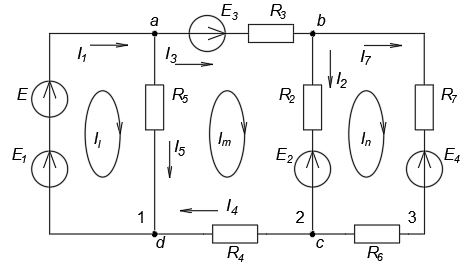 Схема 3. Обозначим действительные токи через контурные по ветвям: I1 = Il; I2 = Im – In; I3 = Im; I4 = Im; I5 = Il – Im; I7 = In . Система уравнений: 1 контур (Il - Im)·R5 = E1 + E; 2 контур Im·( R3+R2+ R4+R5) - Il· R5 - In· R2 = E3 - E2; 3 контур In·( R7+ R6+R2) - Im· R2 = E2 – E4. Решим систему уравнений в программе mathcad: 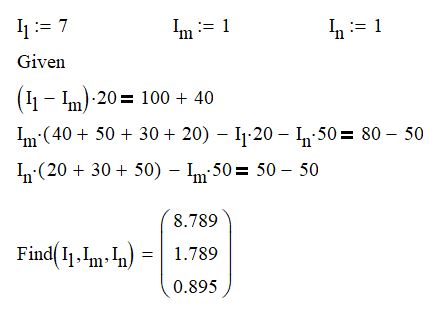 Значения контурных токов: Il = 8,789 А; Im = 1,789 А; In = 0,895 А. Значения токов: I1 = 8,789 А; I2 = 1,789 - 0,895 = 0,895 А; I3 = 1,789 А; I4 = 1,789 А; I5 = 8,789 – 1,789 = 7 А; I7 =0,895 А. Проверка (подставим значения в уравнения по первому закону Кирхгофа): 8,789 - 1,789 – 7 = 0 1,789 - 0,895 - 0,895 = -0,001; 0,895 + 0,895 - 1,789 = 0,001. Погрешность менее 0,1%. 4.2. Расчет методом узловых потенциалов. Заземлим контур в узле d. Обозначим потенциалы в узлах соответственно φa, φb, φc и φd (схема 4).  Схема 4. Где φd =0; φa = E + E1. Токи в ветвях по закону Ома: 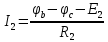 ; ; 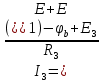 ; ; 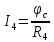 ; ;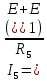 ; ;  . .По первому закону Кирхгофа: 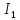 - -  - - 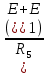 = 0; = 0; - -  - -  = 0; = 0; + +  - - 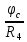 = 0. = 0.Преобразуем систему уравнений: 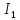 + +  = = 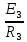 + +  ; ;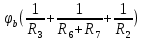 - - 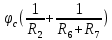 = = 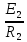 + + 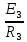 + +  + + 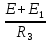 ; ; 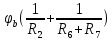 - -  = = 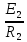 + +  . .Решим систему в mathcad: 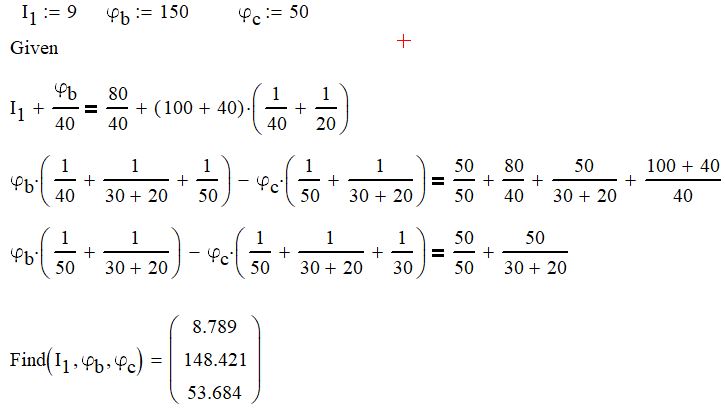 Потенциал узлов φb = 148,421 В, φc = 53,684 В. Токи в ветвях: 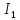 = 8,789 A; = 8,789 A; 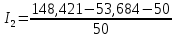 = 0,895 A; = 0,895 A;  = 1,789 А; = 1,789 А;  = 1,789 А; = 1,789 А;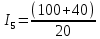 = 7 А; = 7 А; 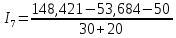 = 0,895 А. = 0,895 А.Полученные значения полностью совпадают с результатами раздела 4.1. 5. Баланс мощностей. Мощность приемников: ΣPпр = ΣI2·R =  = 0,8952·50+1,7892·40+1,7892·30+72·20+0,8952·(30+20) = = 0,8952·50+1,7892·40+1,7892·30+72·20+0,8952·(30+20) = 1286,14 Вт. Мощность источников: ΣЕист = ΣE·I =  = (40+100)·8,789-50·0,895+80·1,789-50·0,895 = 1284,08 Вт. = (40+100)·8,789-50·0,895+80·1,789-50·0,895 = 1284,08 Вт.Погрешность  = 0,005%. = 0,005%.6. Определение тока I3 (ветвь с резистором R3) методом эквивалентного генератора. Удалим ветвь, содержащую R3 (схема 5).   Схема 5. Схема 6. Токи в ветвях:  = 7 A; = 7 A;  = 0. = 0.Напряжение между узлами ab:  = 7·20 - 50 = 90 В. = 7·20 - 50 = 90 В.ЭДС эквивалентного генератора: 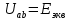 = 90 В. = 90 В.Эквивалентное сопротивление:  ; ;где: Rвн= 0 – внутреннее сопротивление источников Е и Е1.  = 55 Ом. = 55 Ом.К удаленной ветви подсоединяем вместо остальной схемы эквивалентный генератор с параметрами Eэкв и Rэкв (схема 6). Ток в выделенной ветви: 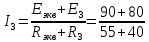 = 1,789 А. = 1,789 А.7. Показания приборов в узлах ab. Напряжение холостого хода 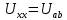 = 90 В. = 90 В.Ток короткого замыкания 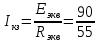 = 1,636 А. = 1,636 А.8. Построение потенциальной диаграммы. Обозначим узлы схемы и составим порядок обхода (схема 7): d-e-a-f-b-g-h-c-d - внешний контур; d-a-f-b-k-c-d – внутренний контур. Объединим оба контура в одну диаграмму d-e-a-f-b-g-h-c-d-a-f-b-k-c-d . 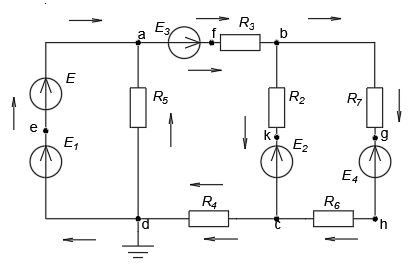 Схема 7. φd = 0; φe = φd + E1 = 0 + 100 = 100 В; φa = 140 В; φf = φa + E3 = 140 + 80 = 220 В; φb = 148,4 В; φg = φb – I7·R7 = 148,4 - 0,895·20 = 130,5 В; φh = φg - E4 = 130,5 – 50 = 80,5 В; φc = 53,7 В φk = φb - I2·R2 = 148,4 - 0,895·50 = 103,5 В. Строим диаграмму (схема 8) где: по горизонтали - сопротивление участка нарастающим итогом (Ом), по вертикали - потенциал узлов (В).  Схема 8 9. Соберем схему в среде multisim. 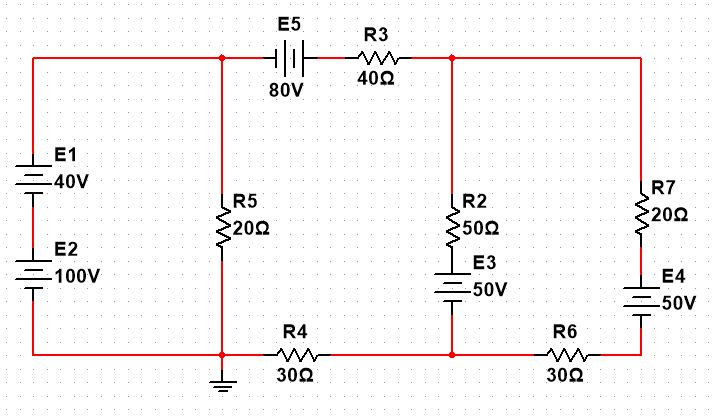 Схема 9. Подключение приемников и источников тока. 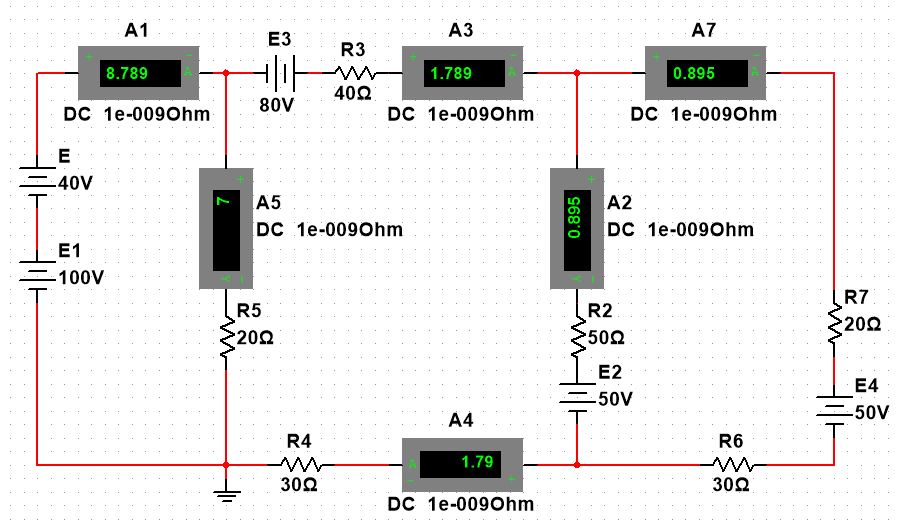 Схема 10. Подключение амперметров. Замер токов в ветвях.  Схема 11. Подключение вольтметров. Замер узловых потенциалов. 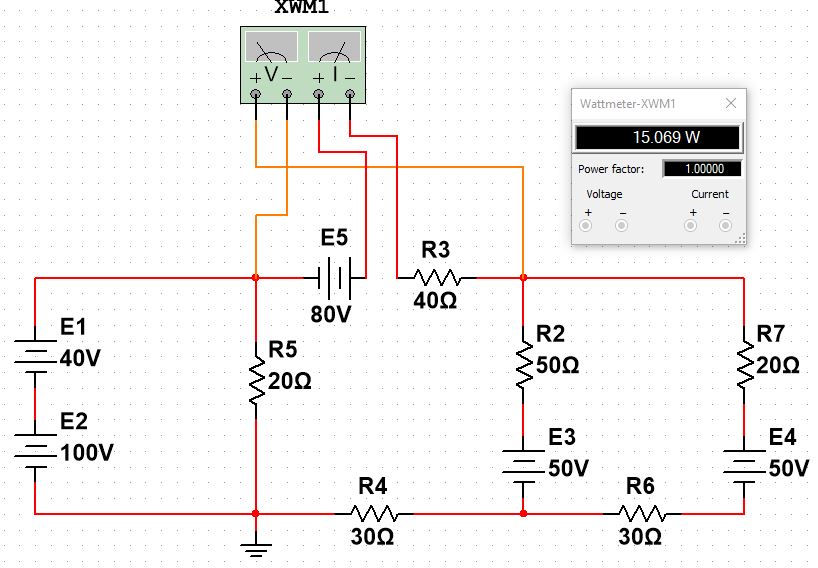 Схема 12. Замер мощности ветви R3. 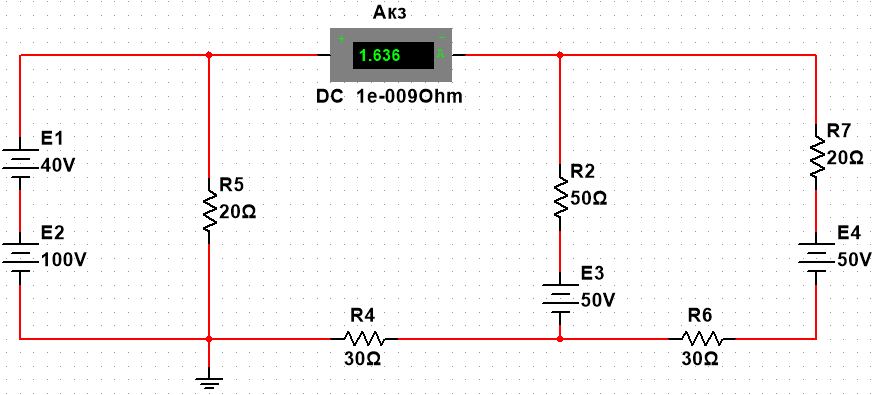 Схема 13. Замер тока короткого замыкания Iкз = 1,636 А. 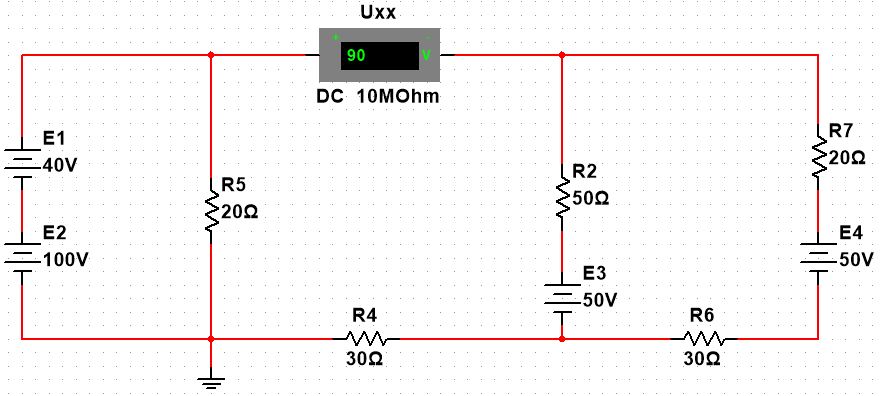 Схема 14. Замер тока холостого хода Uхх = Eэкв = 90 В. Сопротивление Rэкв = Uхх/ Iкз = 90/1,636 = 55 Ом. Ток ветви R3: I3 = (Eэкв+ E3)/ (Rэкв+ R3) = (90+80)/(55+40) = 1,789 А. Показания замеров совпадают с расчетами пункта 6. Выводы: 1. Законы Ома и Кирхгофа достаточны для всех расчетов любого участка электрической цепи. 2. Использование multisim на порядок упрощает проведение расчетов. Благодаря multisim описание схемы стало простым и понятным. 3. Расчеты, полученные аналитическим путем, с высокой степенью точности совпадают с виртуальными показаниями приборов в программе multisim. Литература: 1. Выполнение домашнего задания № 1 первая часть по курсу "Электротехника и электроника". Тема "Расчёт сложной цепи постоянного тока". 2. Бессонов Л.А. Теоретические основы электротехники- М.: Высшая школа, 2012г. 3. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника, -М.: Энергоатомиздат, 1987г. |
