ЗАРЭМА. Дано радc 1c Аналитическое выражение для свободной компоненты 1го тока
 Скачать 426.56 Kb. Скачать 426.56 Kb.
|
|
Дано: 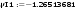 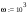 рад/c рад/c 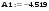 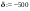 1/c 1/c Аналитическое выражение для свободной компоненты 1-го тока 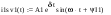 График зависимости свободной компоненты тока, протекающего в 1-й ветви, от времени, приведен на Рис. 1 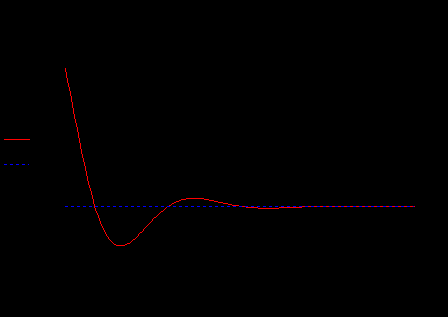 Рис. 1 Аналитическое выражение для принужденной компоненты 1-го тока 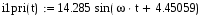 График зависимости принужденной компоненты тока, протекающего в 1-й ветви, от времени, приведен на Рис. 2 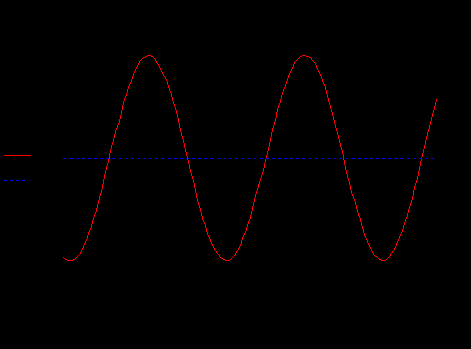 Рис. 2 Аналитическое выражение для тока в первой ветке, как сумма принужденной и свободной компоненты 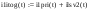 Рис. 3 График зависимости тока, протекающего в 1-й ветке, от времени, построенный в соответствии с принципом суперпозиции, приведен на Рис. 3 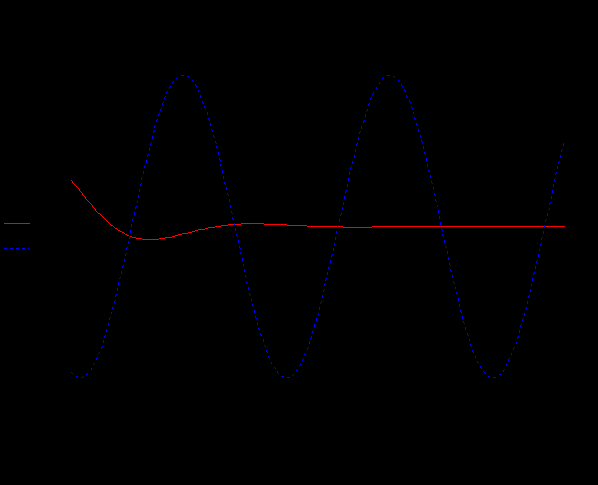 Аналитическое выражение для свободной компоненты 3-го тока 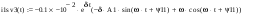 График зависимости свободной компоненты тока, протекающего в 3-й ветви, от времени, приведен на Рис. 4 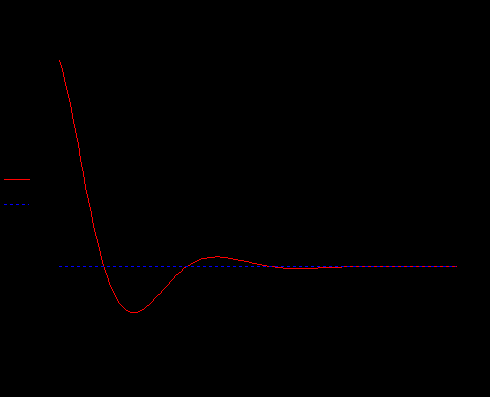 Рис. 4 Аналитическое выражение для принужденной компоненты 3-го тока 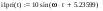 График зависимости принужденной компоненты тока, протекающего в 3-й ветви, от времени, приведен на Рис. 5 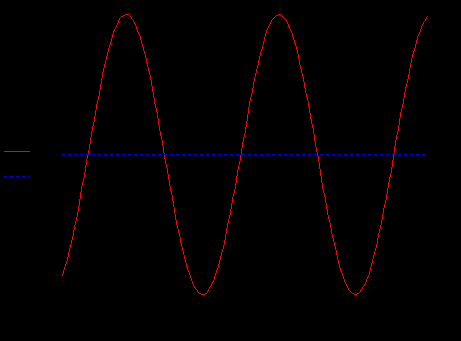 Рис. 5 Аналитическое выражение для тока в третьей ветке, как сумма принужденной и свободной компоненты 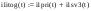 График зависимости тока, протекающего в 3-й ветке, от времени, построенный в соответствии с принципом суперпозиции, приведен на Рис. 6 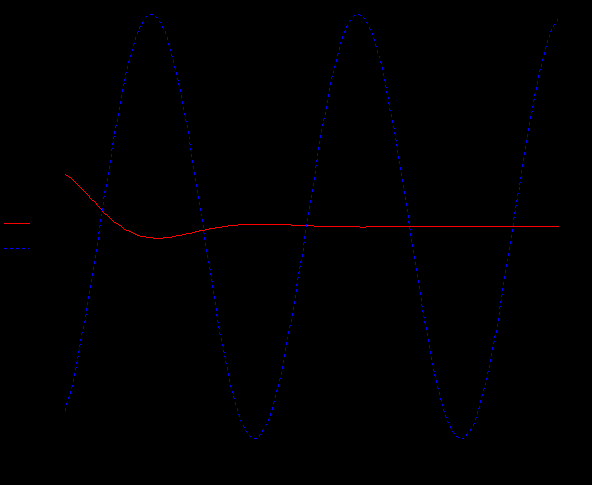 Рис. 6 Аналитическое выражение для свободной компоненты 2-го тока 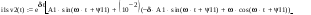 График зависимости свободной компоненты тока, протекающего в 2-й ветви, от времени, приведен на Рис. 7 Рис. 7 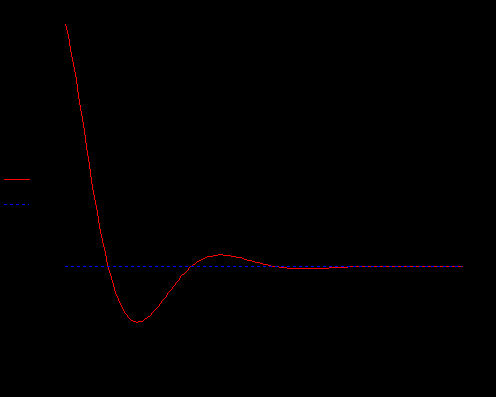 Аналитическое выражение для принужденной компоненты 2-го тока 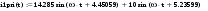 Из законов Кирхгофа следует разность двух искомых токов – ток три и ток два. Таким образом получим график принужденного тока. График зависимости принужденной компоненты тока, протекающего в 2-й ветви, от времени, приведен на Рис. 8 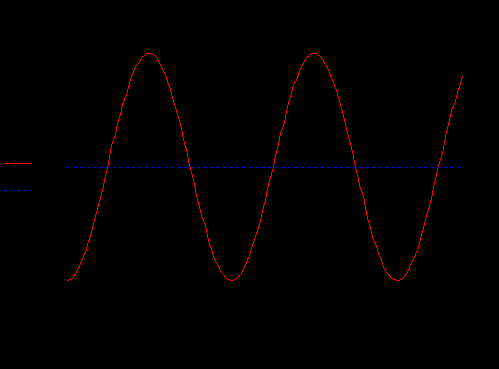 Рис. 8 Аналитическое выражение для тока во второй ветке, как сумма принужденной и свободной компоненты 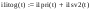 График зависимости тока, протекающего во 2-й ветке, от времени, построенный в соответствии с принципом суперпозиции, приведен на Рис. 9 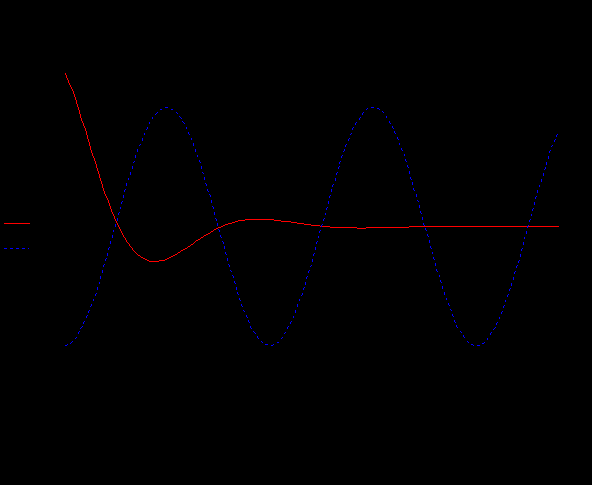 Рис. 9 |
