Дано Решение Найти
 Скачать 289.07 Kb. Скачать 289.07 Kb.
|
|
Задача №1 В центр квадрата, в вершинах которого находятся положительные заряды величиной 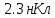 , помещен отрицательный заряд. Найдите значение этого заряда, если результирующая сила, действующая на заряд, равна нулю. , помещен отрицательный заряд. Найдите значение этого заряда, если результирующая сила, действующая на заряд, равна нулю.Дано: Решение 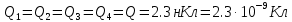 Найти: 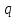 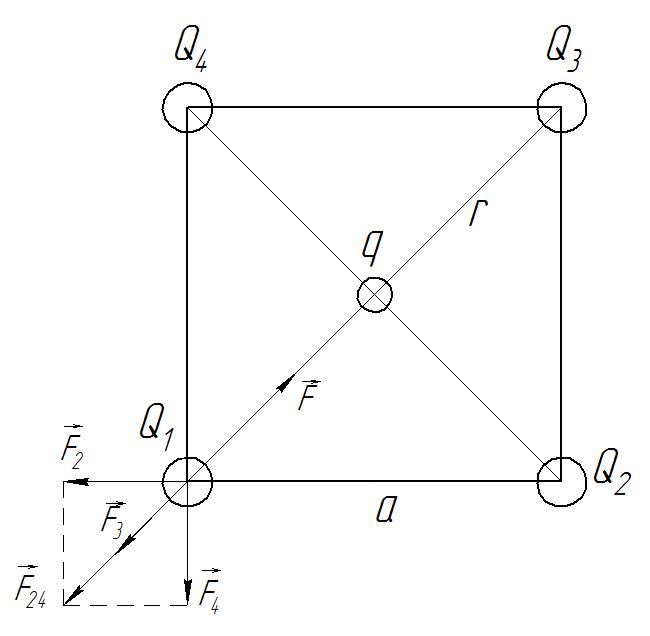 Определим силу, действующую на 1-й заряд со стороны остальных. Суммарная сила будет равна векторной сумме сил, действующих отдельно со стороны 2-го, 3-го и 4-го зарядов и отрицательного заряда 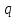 , помещенного в центре квадрата: , помещенного в центре квадрата: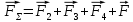 По условию указано, что система должна находиться в равновесии (результирующая сила равна нулю): 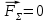 Из соображений симметрии получим, что вектор суммарной силы от зарядов 2 и 4 будет лежать на диагонали квадрата: 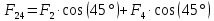 Тогда суммарное значение силы, действующей на первый заряд, будет равно: 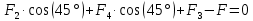 Кулоновская сила взаимодействия двух точечных зарядов определяется по формуле: 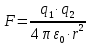 где 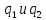 – величины зарядов; – величины зарядов;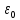 – диэлектрическая постоянная; – диэлектрическая постоянная;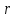 – расстояние между зарядами. – расстояние между зарядами.Тогда силы взаимодействия будут соответственно равны: 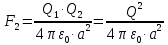 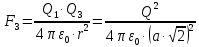 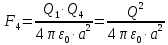 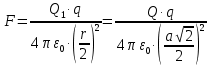 В итоге получим: 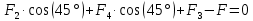 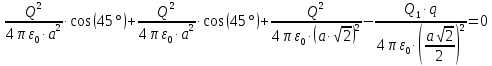 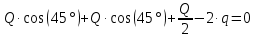 Выразим из полученной формулы значение 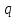 : :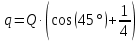 Выполним проверку размерностей: 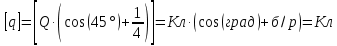 Подставим в полученную формулу числовые значения: 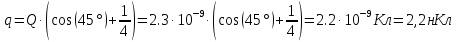 Ответ: 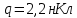 . .Задача №2 Две бесконечно длинные равномерно заряженные нити расположены параллельно друг другу на расстоянии 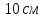 . Найти геометрическое место точек, где результирующая напряженность поля равна нулю, если линейные плотности зарядов нитей имеют значения . Найти геометрическое место точек, где результирующая напряженность поля равна нулю, если линейные плотности зарядов нитей имеют значения 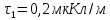 , , 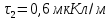 . .Д 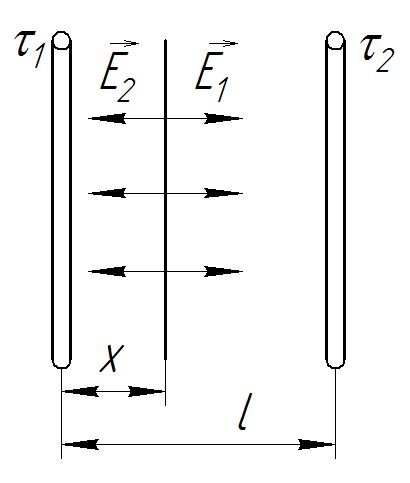 ано: Решение ано: Решение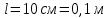 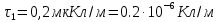 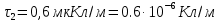 Найти: 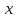 В данном случае указанное геометрическое место точек должно лежать в плоскости, соединяющей две нити, так как только в данной плоскости вектора напряженности электрического поля обеих нитей будут параллельны. При этом искомые точки должны находиться между нитями, чтобы вектора напряженности были противоположно направлены и в сумме давали нулевую напряженность (см. рис.). По определению суммарная напряженность электрического поля равна векторной сумме напряженностей от каждой из нитей: 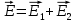 Учтем, что по условию результирующая напряженность должна быть равна нулю. Тогда в проекции получим, 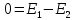 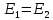 Напряженность электрического поля, создаваемая бесконечно длинной заряженной нитью, определяется по формуле: 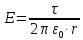 где 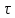 – линейная плотность заряда нити; – линейная плотность заряда нити;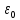 – диэлектрическая постоянная; – диэлектрическая постоянная;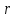 – расстояние от нити до искомой точки. – расстояние от нити до искомой точки.В данном случае, 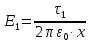 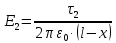 Подставим в исходное выражение: 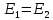 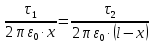 Выразим расстояние 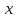 от первой нити до искомого места точек: от первой нити до искомого места точек: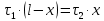 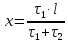 Выполним проверку размерностей: 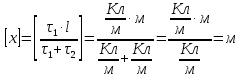 Подставим в полученную формулу числовые значения: 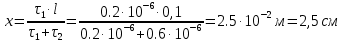 Ответ: 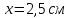 . .Задача №3 Конденсатор емкостью 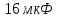 последовательно соединен с конденсатором неизвестной емкости, и оба они подключены к источнику постоянного напряжения последовательно соединен с конденсатором неизвестной емкости, и оба они подключены к источнику постоянного напряжения 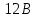 . Определите емкость второго конденсатора, если заряд батареи . Определите емкость второго конденсатора, если заряд батареи 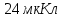 . .Дано: Решение 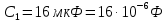 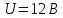 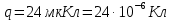 Найти: 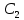 По определению емкость конденсатора 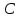 определяется по формуле: определяется по формуле: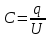 где 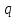 – заряд конденсатора; – заряд конденсатора;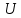 – напряжение на обкладках конденсатора. – напряжение на обкладках конденсатора.Тогда емкость батареи из двух конденсаторов будет равна: 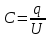 По условию указано, что конденсаторы соединены последовательно. При последовательном соединении конденсаторов итоговая емкость батареи определяется по формуле: 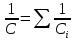 В данном случае, 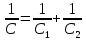 Выразим емкость второго конденсатора: 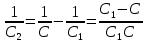 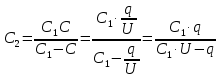 Выполним проверку размерностей: 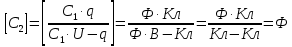 Подставим в полученную формулу числовые значения: 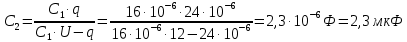 Ответ: 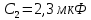 . .Задача №4 В плоском горизонтально расположенном вакуумном конденсаторе капля ртути находится в равновесии. Определите радиус капли, если ее заряд равен 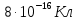 , напряжение на конденсаторе , напряжение на конденсаторе 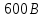 , расстояние между пластинами , расстояние между пластинами 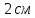 . .Д 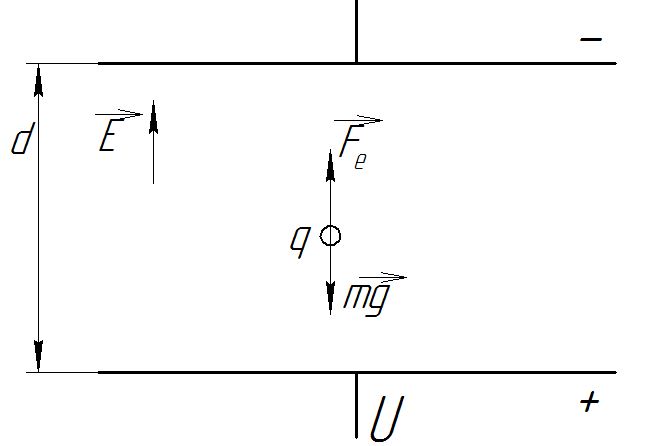 ано: Решение ано: Решение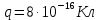 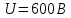 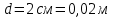 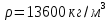 Найти: 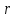 На каплю ртути действует сила тяжести 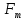 и сила и сила 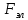 со стороны электрического поля. По условию капля находится в равновесии. Следовательно, указанные две силы уравновешивают друг друга: со стороны электрического поля. По условию капля находится в равновесии. Следовательно, указанные две силы уравновешивают друг друга: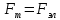 Сила тяжести по определению равна: 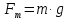 где 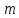 – масса капли; – масса капли;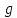 – ускорение свободного падения. – ускорение свободного падения.Масса капли определяется выражением: 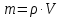 где 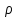 – плотность ртути; – плотность ртути;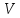 – объем капли. – объем капли.Будем считать, что капля имеет форму шара с радиусом 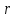 . Тогда из геометрических соображений объем капли равен объему шара: . Тогда из геометрических соображений объем капли равен объему шара: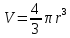 Сила, с которой электрическое поле действует на точеный заряд 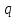 , определяется выражением: , определяется выражением: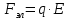 где 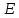 – величина напряженности электрического поля. – величина напряженности электрического поля.Электрическое поле плоского конденсатора можно считать однородным. Тогда напряженность электрического поля в конденсаторе связана с его параметрами соотношением: 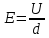 где 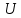 – напряжение на конденсаторе; – напряжение на конденсаторе;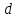 – расстояние между обкладками конденсатора. – расстояние между обкладками конденсатора.Подставим все полученные выше формулы в исходную: 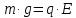 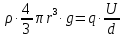 Выразим из полученного соотношения радиус капли: 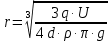 Выполним проверку размерностей: 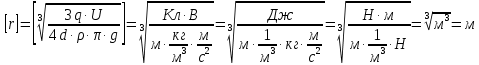 Подставим в полученную формулу числовые значения: 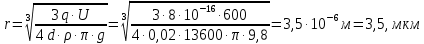 Ответ: 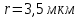 . .Задача №5 В цепь включены: элемент с ЭДС – 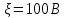 и внутренним сопротивлением и внутренним сопротивлением 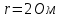 ; сопротивления ; сопротивления 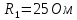 и и 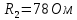 . На сопротивлении . На сопротивлении 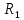 выделяется мощность выделяется мощность 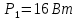 . Какой ток . Какой ток 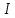 показывает амперметр? показывает амперметр?Д  ано: Решение ано: Решение     Найти:  По условию указано, что на сопротивлении  выделяется мощность выделяется мощность 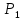 : :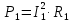 где 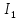 – сила тока через сопротивление – сила тока через сопротивление 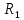 . .Тогда сила тока 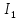 будет равна: будет равна: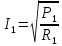 Из схемы видно, что сопротивления 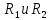 соединены параллельно. Тогда напряжения на данных сопротивлениях будут одинаковыми: соединены параллельно. Тогда напряжения на данных сопротивлениях будут одинаковыми: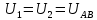 По закону Ома для участка цепи получим:   Тогда сила тока через сопротивление  будет равна: будет равна: Согласно первому закону Кирхгофа ток через сопротивление 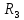 , а, следовательно, и через амперметр, будет равен: , а, следовательно, и через амперметр, будет равен: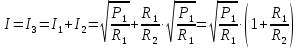 Выполним проверку размерностей: 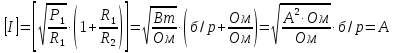 Подставим в полученную формулу числовые значения: 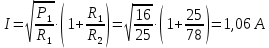 Ответ:  . .Задача №6 Два параллельных бесконечно длинных провода, по которым текут противоположно направленные токи силой 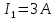 и и 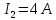 , расположены на расстоянии , расположены на расстоянии 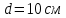 друг от друга. Определите магнитную индукцию поля и напряженность в точке, находящейся посередине между проводами. Определить силу, действующую на единицу длины проводов. друг от друга. Определите магнитную индукцию поля и напряженность в точке, находящейся посередине между проводами. Определить силу, действующую на единицу длины проводов.Д 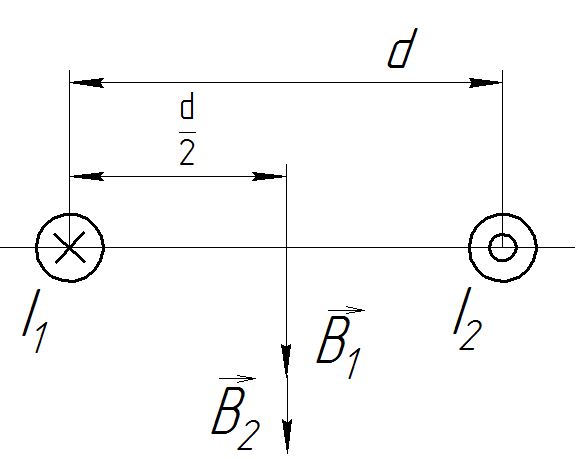 ано: Решение ано: Решение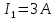 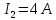 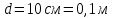 Найти:  По определению суммарная величина магнитной индукции равна векторной сумме магнитных индукций, создаваемых в искомой точке каждым из проводов в отдельности:  Определим направление векторов  в искомой точке. Согласно правилу правого винта оба вектора будут сонаправлены (см. рис.). Тогда итоговая величина магнитной индукции будет равна: в искомой точке. Согласно правилу правого винта оба вектора будут сонаправлены (см. рис.). Тогда итоговая величина магнитной индукции будет равна: Магнитная индукция, создаваемая бесконечно длинным проводником с током, определяется по формуле: 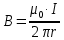 где 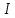 – сила тока в проводнике; – сила тока в проводнике;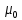 – магнитная постоянная; – магнитная постоянная;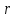 – расстояние от проводника до искомой точки. – расстояние от проводника до искомой точки.В данном случае получим, 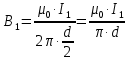 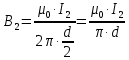 Подставим в исходную формулу: 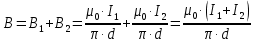 Магнитная индукция 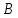 связана с напряженностью магнитного поля связана с напряженностью магнитного поля 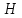 соотношением: соотношением: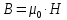 Выразим напряженность магнитного поля: 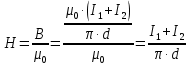 По определению сила, с которой взаимодействуют два параллельных проводника с током, равна: 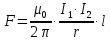 где 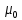 – магнитная индукция; – магнитная индукция;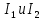 – силы токов в проводниках; – силы токов в проводниках;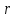 – расстояние между проводниками; – расстояние между проводниками;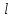 – длины, взаимодействующих проводников. – длины, взаимодействующих проводников.Тогда сила взаимодействия на единицу длины будет равна: 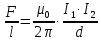 Выполним проверку размерностей: 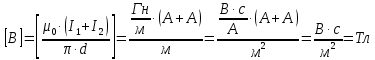 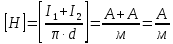 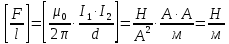 Подставим в полученные формулы числовые значения:    Ответ:  , , 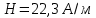 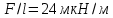 . .Задача №7 Замкнутый на себя соленоид радиусом 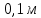 , содержащий , содержащий 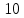 витков, вращается с угловой скоростью витков, вращается с угловой скоростью 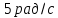 вокруг диаметра одного из витков в однородном магнитном поле с индукцией вокруг диаметра одного из витков в однородном магнитном поле с индукцией 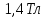 . Ось вращения перпендикулярна вектору магнитной индукции. Сопротивление соленоида – . Ось вращения перпендикулярна вектору магнитной индукции. Сопротивление соленоида – 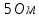 , индуктивность , индуктивность 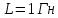 . Определить максимальную силу тока, текущую через соленоид. . Определить максимальную силу тока, текущую через соленоид.Д  ано: Решение ано: Решение      Найти:  Определим изменение потока через один виток рамки. Магнитный поток через контур определяется по формуле: 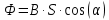 где 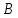 – величина индукции магнитного поля; – величина индукции магнитного поля;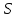 – площадь контура; – площадь контура;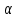 – угол между вектором индукции и нормалью к плоскости контура. – угол между вектором индукции и нормалью к плоскости контура.В данном случае магнитный поток через катушку будет изменяться во времени за счет поворота катушки и изменения площади, которую пронизывает магнитное поле: 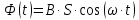 где 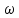 – угловая скорость вращения катушки. – угловая скорость вращения катушки.Площадь витка рамки будет равна: 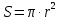 Учтем, что рамка содержит 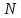 витков. Тогда, витков. Тогда,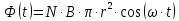 Запишем закон электромагнитной индукции Фарадея: 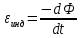 где 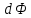 – изменение магнитного потока через контур. – изменение магнитного потока через контур.Подставим полученную выше формулу для магнитного потока в закон электромагнитной индукции Фарадея и выполним преобразования: 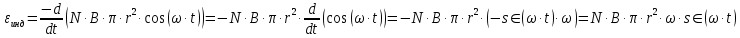 В итоге получим, 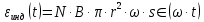 По условию указано, что соленоид замкнут сам на себя. Следовательно, соленоид можно представить как электрическую схему, состоящую из последовательно соединенных сопротивления 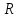 и индуктивности и индуктивности 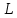 , и подключенную к переменному напряжению (см. рис.) , и подключенную к переменному напряжению (см. рис.)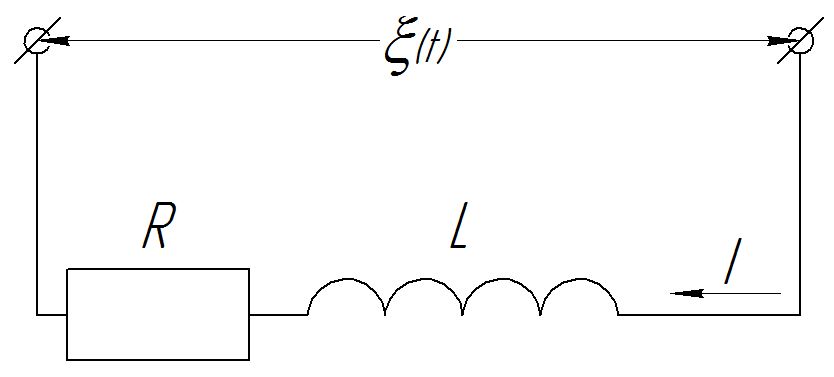 Согласно закону Ома сила тока в данном контуре будет равна:  где  – полное сопротивление цепи. – полное сопротивление цепи.Полное сопротивление цепи будет равно:  где  – величина индуктивного сопротивления. – величина индуктивного сопротивления. где  – циклическая частота внешнего напряжения; – циклическая частота внешнего напряжения; – индуктивность катушки. – индуктивность катушки.В итоге получим,  По условию требуется определить максимальное значение силы тока: 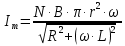 Выполним проверку размерностей: 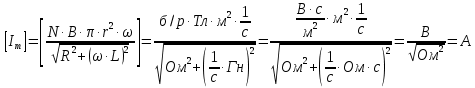 Подставим в полученную формулу числовые значения: 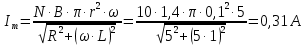 Ответ: 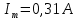 . .Задача №8 В цепь переменного тока с частотой 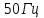 включены последовательно индуктивность включены последовательно индуктивность 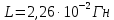 и активное сопротивление и активное сопротивление 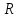 . Найдите величину . Найдите величину 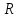 , если известно, что сдвиг по фазе между током и напряжением равен , если известно, что сдвиг по фазе между током и напряжением равен  . .Дано: Решение    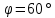 Найти: 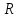 По условию указано, что цепь соединена последовательно. Следовательно, ток через все элементы будет протекать одинаковый: 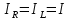 Полное напряжение в цепи будет складываться из напряжения на активном сопротивлении 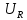 и напряжения на катушке индуктивности и напряжения на катушке индуктивности 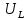 , которое будет опережать ток на , которое будет опережать ток на 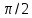 (см. рис.). Сдвиг по фазе между напряжением и силой тока из геометрических соображений будет равен: (см. рис.). Сдвиг по фазе между напряжением и силой тока из геометрических соображений будет равен: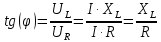 где 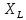 – величина индуктивного сопротивления. – величина индуктивного сопротивления.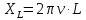 где 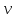 – частота внешнего напряжения; – частота внешнего напряжения;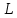 – индуктивность катушки. – индуктивность катушки.Выразим из полученного соотношения сопротивление 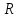 . .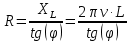 Выполним проверку размерностей: 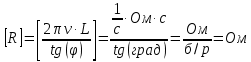 Подставим в полученные формулы числовые значения: 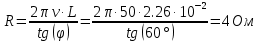 Ответ: 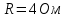 . . |
