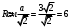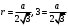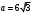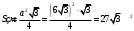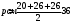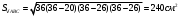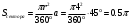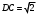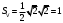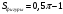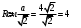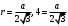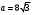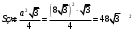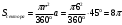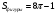соч 9 класс 4 четверть геометрия (1). Дата 16. 05 Соч 4 четверть 9 В класс Ф. И. учащегося задания

• Название: Дата 16. 05 Соч 4 четверть 9 В класс Ф. И. учащегося задания
• Дата: 16.05.2023
• Размер: 1.69 Mb.
• Имя файла: соч 9 класс 4 четверть геометрия (1).docx
• Тип: Документы; #1136524

Дата: 16.05 СОЧ 4 четверть

9 «В» класс Ф.И.учащегося _________________________________

ЗАДАНИЯ

1 ВАРИАНТ

Оценивание заданий работы
№ задания	1	2	3	4	5	6
Количество баллов	1	1	4	4	5	5
Всего баллов	20 баллов

1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1440°.

А) 8 В) 9 С) 10 D) 12

2. Дана окружность радиуса 10 см . Чему равна длина ее дуги с градусной мерой 90°?

А) 4 см В) 6 см С) 8 см D) 5 см

3. Три угла четырехугольника, вписанного в окружность, взятые в порядке следования, относятся как 4 : 3 : 5. Найдите углы четырехугольника.

4. В окружность вписан квадрат со стороной 3 √2 см. Найдите площадь правильного треугольника, описанного около этой окружности.

5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.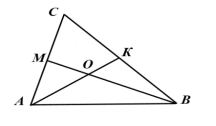



6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 4 см. ОD = 2 см и DOС  45°. Найдите площадь закрашенной области.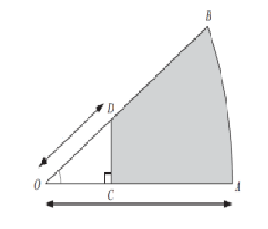



Схема выставления баллов

1 вариант

№	Ответ	Балл	Дополнительная информация
1	С	1
2	D	1
3	4х + 5х = 180°	1
	х = 20°	1
	80°, 60°, 100°	1
	180° – 60° = 120°	1
4		1
		1	Принимается альтернативное решение
		1
		1
5	АО=2х, ОК=х  2х  х  30 или ВО=2х,ОМ=х  2х  х  39	1	Применяет свойство медиан треугольника
	АО = 20 см и ВО = 26 см	1
	Полупериметр	1
		1
	SABC 3240  720 см2	1	Применяет свойство медиан треугольника
6		1
	DC=DOsin450	1	Принимается альтернативное решение
		1
		1
		1
Итого:		20

Дата: 16.05 СОЧ 4 четверть

9 «В» класс Ф.И.учащегося _________________________________

2 ВАРИАНТ

Оценивание заданий работы
№ задания	1	2	3	4	5	6
Количество баллов	1	1	4	4	5	5
Всего баллов	20 баллов

1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1980°.

А) 18 В) 13 С) 12 D) 11

2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 90°?

А) 4 см В) 6 см С) 8 см D) 12 см


3. Три угла четырехугольника, вписанного в окружность, взятые в порядке следования, относятся как 2 : 6 : 7. Найдите углы четырехугольника.

4. В окружность вписан квадрат со стороной 4√2 см. Найдите площадь правильного треугольника, описанного около этой окружности.

5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.



6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 8 см. ОD = 2 см и DOС  45°. Найдите площадь закрашенной области.



Схема выставления баллов

2 вариант

№	Ответ	Балл	Дополнительная информация
1	B	1
2	B	1
3	2х + 7х = 180°	1
	х = 20°	1
	40°, 120°, 140°	1
	180° – 120° = 60°	1
4		1
		1	Принимается альтернативное решение
		1
		1
5	АО=2х, ОК=х  2х  х  30 или ВО=2х,ОМ=х  2х  х  39	1	Применяет свойство медиан треугольника
	АО = 20 см и ВО = 26 см	1
	Полупериметр	1
		1
	SABC 3240  720 см2	1	Применяет свойство медиан треугольника
6		1
	DC=DOsin450	1	Принимается альтернативное решение
		1
		1
		1
Итого:		20

1, (n-2)*180=1440
n-2=8
n=10-десятиугольник(десять сторон)

2,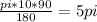



3,Для решения обозначим углы  

четырёхугольника буквами ADCD.

Тогда можно записать:

∠A:∠B:∠C=4:3:5.

В четырёхугольнике, вписанном в окружность,  

сумма противоположных углов равна 180°, то есть:

∠A+∠C=180°, ∠B+∠D=180°.

Иными словами на ∠D приходится:

(∠А+∠С)-∠В=(4+5)-3=6 частей.

На 1 часть приходится:

180°:(4+5)=180°(3+6)=20°.

∠A=20°*4=80°;

∠B=20°*3=60°;

∠C=20°*5=100°;

∠D=20°*6=120°.

4, В окружность вписан квадрат со стороной 3 √2 см. Найдите площадь правильного треугольника, описанного около этой окружности.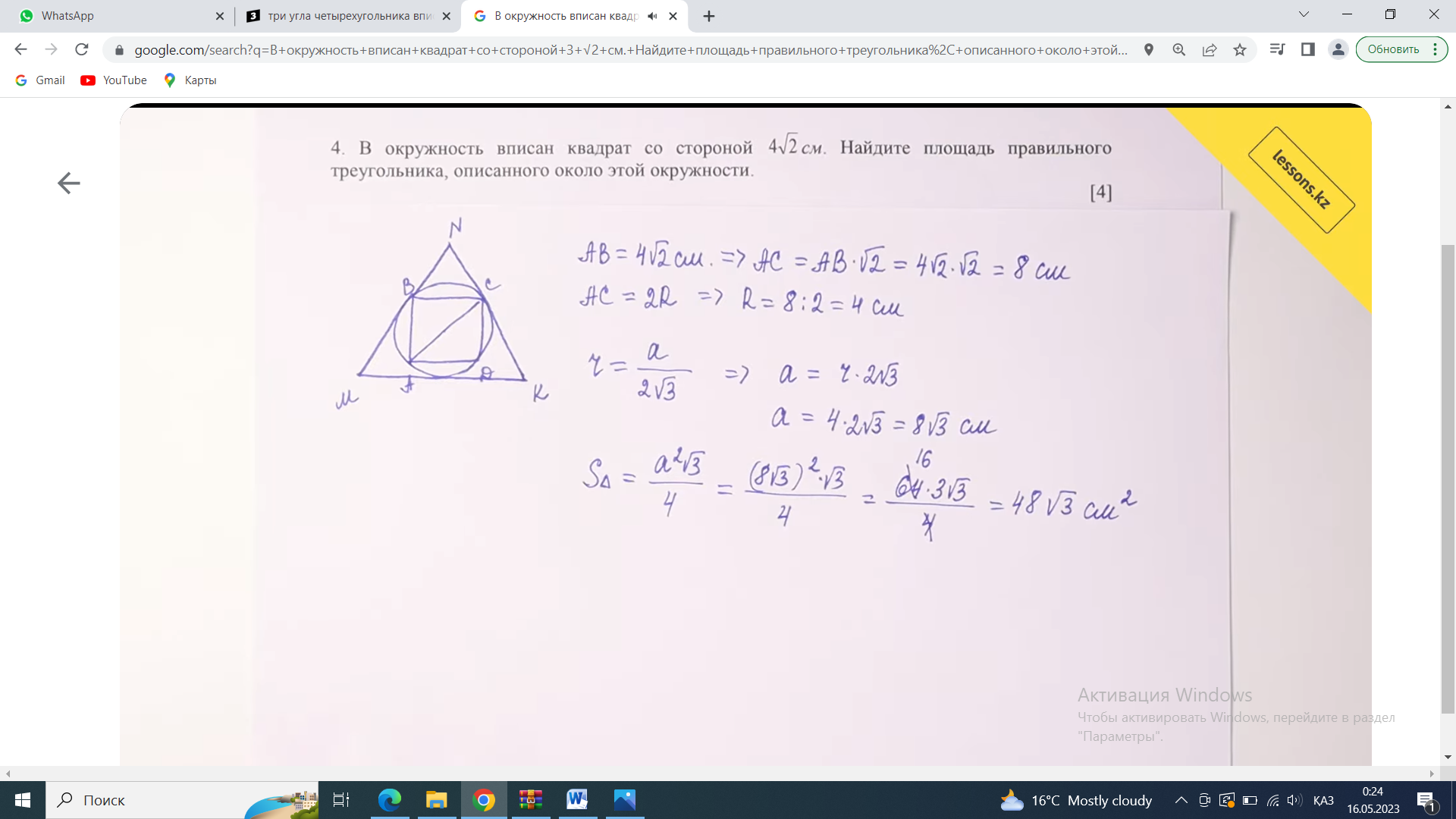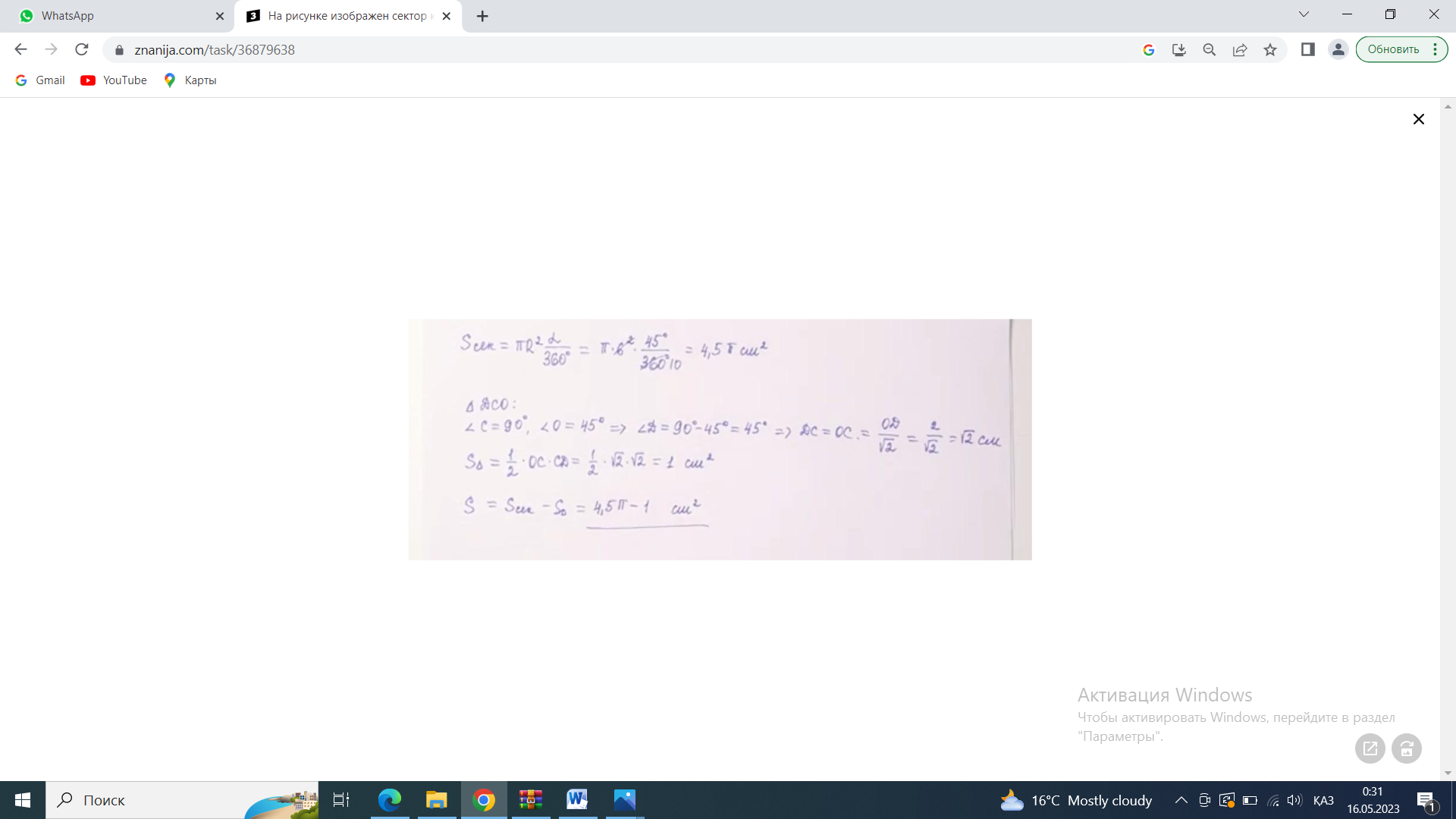









Найдём сначала площадь всего сектора:

Воспользуемся формулой площади круга, и умножим на 1/8 , т.к. этот сектор составляет 1/8 часть всего круга (360/45 = 8)

S= 

S= 2Pi

Найдём площадь прямоугольного треугольника:

S=1/2 a* b

Необходимо найти катеты.

Т.к. ∠DOC = 45° , то и ∠ODC = 45° ⇒

Δ- равнобедренный и его катеты равны. ⇒

По теореме Пифагора: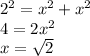



S = 1/2 * 

S = 1

Находим площадь закрашенной фигуры:

S = 2Pi - 1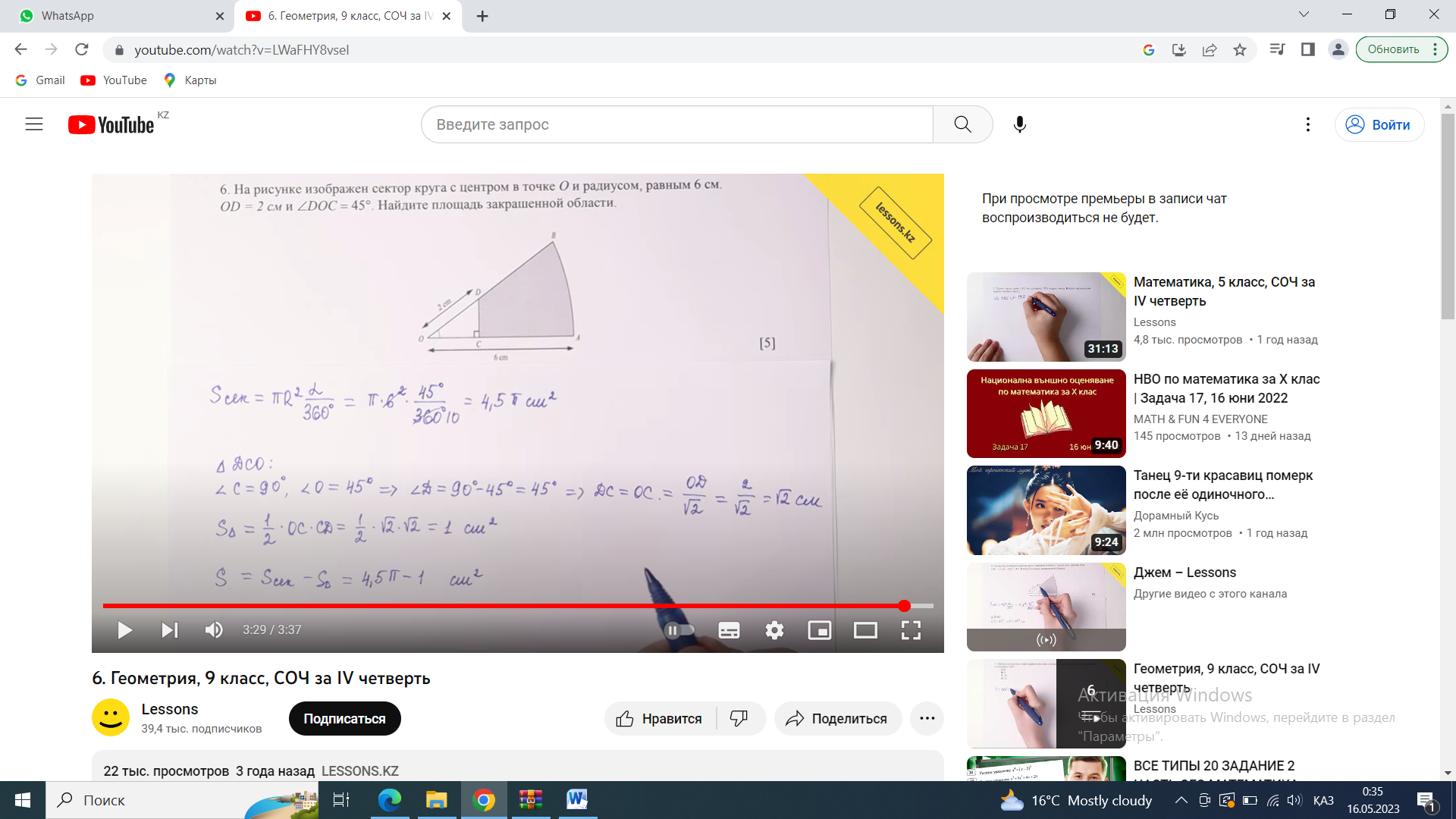