Практическая работа Денисенко А.П. 2101-0500-2101858. Денисенко Андрей Павлович

• Название: Денисенко Андрей Павлович
• Дата: 23.10.2022
• Размер: 96.12 Kb.
• Имя файла: Практическая работа Денисенко А.П. 2101-0500-2101858.docx
• Тип: Документы; #749301

Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	математика

дисциплине

Выполнил(а) студент(ка)	Денисенко Андрей Павлович
			фамилия имя отчество
Идентификационный номер:		2101-0500-2101858

Пермь 2022

Задание 1. Решить систему линейных алгебраических уравнений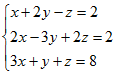


Решение.

Решим систему линейных алгебраических уравнений по формулам Крамера.

Вычислим главный определитель.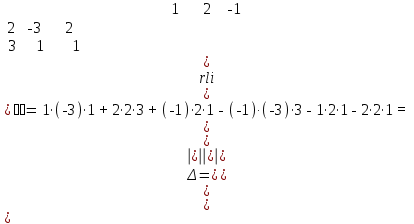



Главный определитель не равен нулю, значит, система имеет единственное решение.

Вычислим вспомогательные определители _.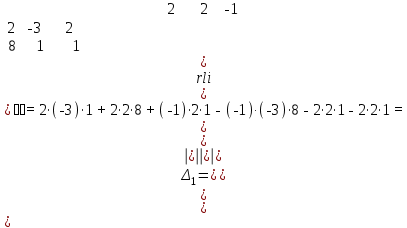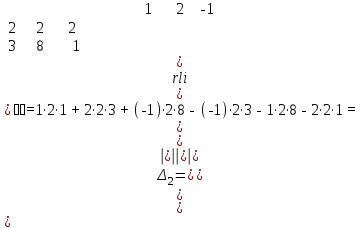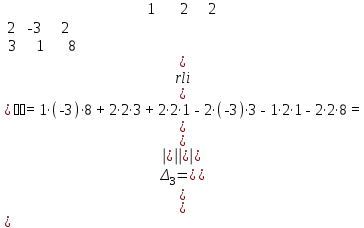







По формулам Крамера находим решение системы: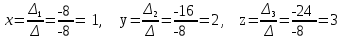



Ответ: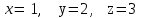

Задание 2. Дано z₁ = 5 – 4i   и   z₂ = –1 – i. Выполнить действия:
А) z₁+ z₂;  Б) z₁ × z₂;  В) z₁ / z₂.
Решение.
А) 5 – 4i + (–1) – i = 4 - 5i



Ответ : 4-5i
Б) (5 – 4i)*(–1 – i ) = -5 - 5i + 4i – 4 = 9 - i
Ответ : 9 - i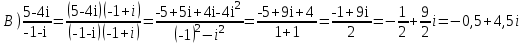

Ответ : 0.5-4.5i

Задание 3. Найти математическое ожидание и дисперсию, заданной законом распределения

Х	‒5	2	3	4
Р	0,4	0,3	0,1	0,2

Решение.
Найдем математическое ожидание: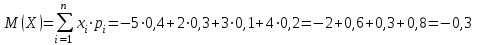



Дисперсию находим по формуле: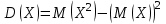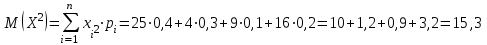




Найдем дисперсию: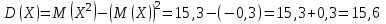


Ответ: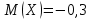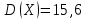

Задание 4.  Вычислить предел 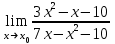     при x₀=2.
Решение.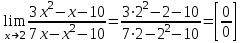



Разложим числитель и знаменатель дроби на множители.

Воспользуемся формулой разложения на множители квадратного трехчлена:

ах² +bх + c = а(х – х₁)(х – х₂),

где х₁ и х₂ – корни квадратного уравнения ах² +bх + c = 0.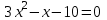

;

D = b² – 4ac = (-1)² – 4∙3∙ (– 10) = 1 + 120 = 121.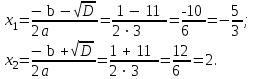



Таким образом, получаем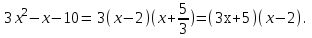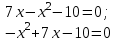





D = b² – 4ac = 7² – 4∙(-1) ∙ (–10) = 49 - 40 = 9.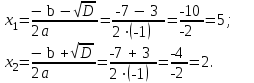



Таким образом, получаем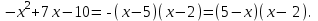



Исходный предел запишем в виде: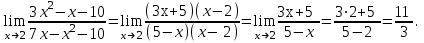



Ответ: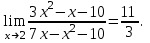
Задание 5. Найти производную функции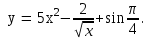 
Решение.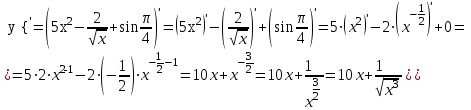



Ответ: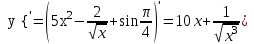

Задание 6. Вычислить неопределенный интеграл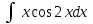  

Решение.
Воспользуемся формулой: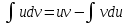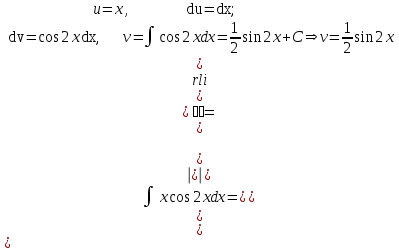




Ответ: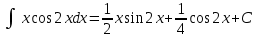