1. Егер кез келген 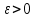 болғанда болғанда 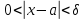 теңсіздігін қанағаттандыратын кез келген теңсіздігін қанағаттандыратын кез келген 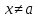 үшін үшін 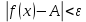 теңсіздігі орындалатындай теңсіздігі орындалатындай 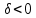 табылса, ондаA саны x айнымалысының а санына ұмтылғандағы табылса, ондаA саны x айнымалысының а санына ұмтылғандағы 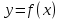 .….деп аталады. .….деп аталады. 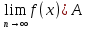
|
А) тізбегінің шегі
|
2. Егер х айнымалысы а санына ұмтылған кезде х тек қана а-дан үлкен мәндерді қабылдаған жағдайда 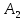 саны саны 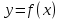 функциясының шегі болса, онда функциясының шегі болса, онда 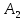 саны саны 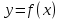 функциясының а нүктесіндегі …деп аталады. функциясының а нүктесіндегі …деп аталады. 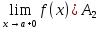
|
B) сол жақ шегі
|
3. Егер n- натурал сан болса, онда мына теңдіктер орындалады
|
C)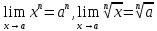
|
4.Егер х айнымалысы а санына ұмтылғанда y=f(x) және y=g(x) функцияларының шектері бар болса, онда олардың қосындысының да шегі бар болады және ол шек функциялардың шектерінің қосындысына тең:
|
D)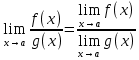
|
5.Егер кез келген 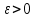 үшін үшін 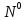 саны табылса, саны табылса, 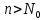 теңсіздігін қанағаттандыратын кез келген nмәндері үшін теңсіздігін қанағаттандыратын кез келген nмәндері үшін 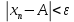 теңсіздігі орындалса, онда Aсаны n шексіздікке ұмтылғандағы теңсіздігі орындалса, онда Aсаны n шексіздікке ұмтылғандағы 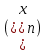 …….деп аталады. …….деп аталады.
|
E) функциясының шегі
|
6. Функцияның шегін тап: 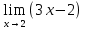
|
F) анықталмағандықты ашу
|
7.Егер х айнымалысы а санына ұмтылған кезде х тек қана а-дан кіші мәндерді қабылдаған жағдайда 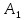 саны саны 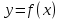 функциясының шегі болса, онда функциясының шегі болса, онда 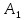 саны саны 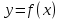 функциясының а нүктесіндегі …деп аталады. функциясының а нүктесіндегі …деп аталады. 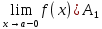
|
G)4
|
8. Егер 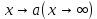 ұмтылғанда анықталмағандықты беретін функцияның шегін табу…деп аталады. ұмтылғанда анықталмағандықты беретін функцияның шегін табу…деп аталады.
|
H) оң жақ шегі
|
9.Егер х айнымалысы а санына ұмтылғанда y=f(x) және y=g(x) функцияларының шектері бар және 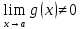 болса, онда олардың қатынасының да шегі бар болады және ол шек функциялардың қатынасына тең: болса, онда олардың қатынасының да шегі бар болады және ол шек функциялардың қатынасына тең:
|
I)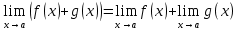
|
10. Функцияның шегін тап: 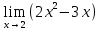
|
J) 2
|
 Скачать 22.92 Kb.
Скачать 22.92 Kb.