Разбивка кривых. Детальная+разбивка+кривых+различными+методами+СРОП (2). Детальная разбивка кривых различными методами
 Скачать 134.54 Kb. Скачать 134.54 Kb.
|
|
Детальная разбивка кривых различными методами В лабораторной работе рассмотрен метод прямоугольных координат. 8.1 Исходные данные. Целью настоящей работы является определение координат главных и промежуточных точек круговой кривой, составление плана и перенесении их в натуру. Данные для решения задачи: 8.1.1 Угол поворота трассы q°:
8.1.2 Координаты точки начала кривой (НК) и дирекционный угол трассы АС:
8.1.3 Прямоугольные координаты Х и У определить для каждого 5-ти метрового участка кривой. 8.2 Методические указания: 8.2.1 Необходимо вычислить следующие элементы круговой кривой по формулам: Тангенс – длина касательной 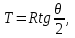 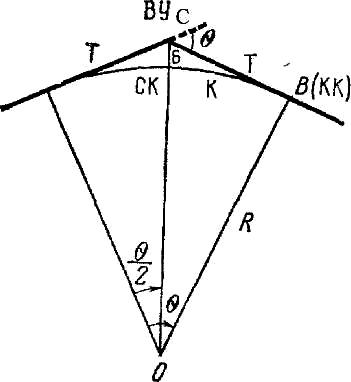 Биссектриса Б = СО – R = Rsec Биссектриса Б = СО – R = Rsec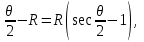 Длина кривой 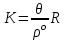 , ,Домер Д = 2Т – К Рисунок 8.1 8.2.2 Следует определить координаты точек середины и конца кривой, вершины угла поворота, а также точки О. Составить план разбивки круговой кривой в масштабе 1: 1000. 8.3 Выполнить детальную разбивку горизонтальной кривой, для этого: 8.3.1 Вычислить величину угла Өо, соответствующего заданной дуге Кгор: Өо = 180 х Кгор/ 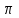 R = Кгор х 0,017453/ R, R = Кгор х 0,017453/ R,где 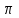 = 3,14. = 3,14.8.3.2 Приняв начало координат в точке НК, касательную НК – ВУ за ось абсцисс, а линию НК – О за ось ординат, вычисляют координаты точек кривой до ее середины (СК) по формулам: Х1 = RsinӨо; Y1 = R(1 – cosӨо); Х2 = Rsin2Өо; Y2= R(1 – cos2Өо); Х3 = Rsin3Өо. Y3= R(1 – cos3Өо). и т.д. 8.3.3 Для контроля правильности вычислений аналогичные расчеты координат точек кривой производят от конца кривой (КК), приняв его за начало координат. 8.3.4 Результаты расчетов должны быть представлены в виде таблицы. 8.3.5 На план разбивки круговой кривой в масштабе 1: 1000 нанести точки круговой кривой по соответствующим координатам. 8.3.6 На местности выполнить вынос в натуру основных элементов круговой кривой и ее детальную разбивку 8.3.6 Самостоятельно выполнить детальную разбивку круговой кривой способом продолженных хорд и углов и хорд. Способ продолженных хорд (рисунок 8.2). Точку В на кривой определяют линейной засечкой из точек А и В', откладывая из точки А лентой хорду d и рулеткой из точки В' отрезок у. Точку В' определяют путем откладывания по оси абсцисс хорды d. По направлению АВ (продолжение хорды) откладывают хорду d и получают точку С'. Отложив от точки В хорду d и от С' отрезок к линейной засечкой получают точку С и т.д. Из подобных треугольников ОВС и ВС'С получают: 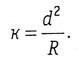 Так как в треугольнике АВ'В угол В'АВ равен φ/2, то можно считать у = к/2. 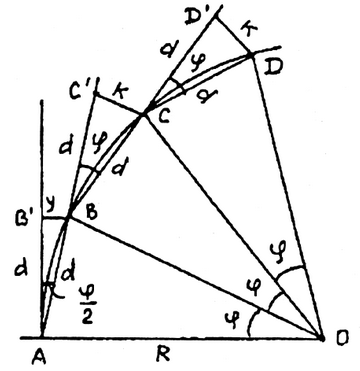 Рисунок 8.2 – Способ продолженных хорд Способ углов и хорд основывается на том, что углы с вершиной в какой-либо точке круговой кривой, образованные касательной и секущей и заключающие равные дуги, равны половине соответствующего центрального угла (рисунок 8.3). Для разбивки кривой при помощи углов и хорд вычисляют центральный угол Рассчитывают углы С 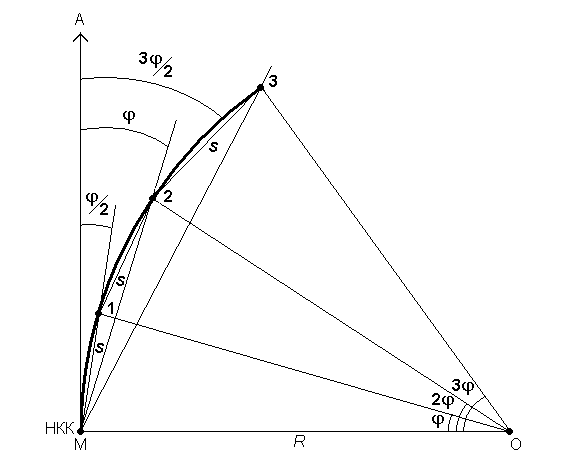 начала выполняют разбивку кривой от её начала НКК до середины СКК. Затем, освободив алидаду, в сторону кривой откладывают от тангенса угол начала выполняют разбивку кривой от её начала НКК до середины СКК. Затем, освободив алидаду, в сторону кривой откладывают от тангенса угол Рисунок 8.3 – Способ углов и хорд | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
