CorrelatorШПС. Детектирование когерентное или автокорреляционное с использованием
 Скачать 1.8 Mb. Скачать 1.8 Mb.
|
|
Детектирование: когерентное или автокорреляционное с использованием: – синхронного детектора, – корреляционного приемника, – согласованного фильтра Сигналы равной частоты когерентны, если их начальные фазы априорно известны Корреляционный приемник Корреляционный приемник обнаруживает и идентифицирует сигнал s(t), сравнивая его с опорным (образцовым) сигналом или с набором образцовых сигналов soi(t), представляющих различные символы сообщения. При случайной помехе типа белого гауссова шума вероятность ошибочного решения минимальна, если сигналы сравниваются по критерию минимума среднеквадратичного отклонения (СКО): 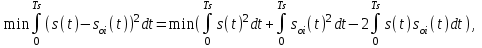 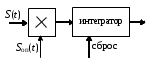 Коэффициент взаимной корреляции сигналов 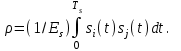 принимает значения от –1 до 1. При идентичных сигналах ρ = 1. Сигналы противоположны, если ρ = –1, и ортогональны, если ρ = 0. Примеры противоположных и ортогональных сигналов  Понятие согласованного фильтра Согласованный фильтр применяется для обнаружения сигнала известной формы x(t). Отклик СФ на сигнал x(t), с которым он согласован, принимает в момент окончания сигнала x(t) максимально возможное значение, пропорциональное энергии сигнала Ex, и не зависит от формы сигнала. Выходной сигнал фильтра 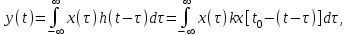 Интеграл от произведения двух функций максимален, если эти функции пропорциональны друг другу. Условие максимума в момент времени t0 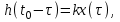 или или 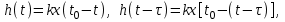 т.е. т.е. импульсная характеристика СФ – зеркальная копия входного сигнала x(t).  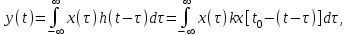 т.е. отклик на сигнал x(t) пропорционален его автокорреляционной функции. 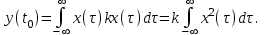 т.е. максимальное значение сигнала на выходе СФ в момент t0, пропорционально энергии сигнала x(t). Комплексный коэффициент передачи СФ 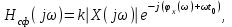 СФ усиливает мощные гармоники сигнала сильнее, чем слабые гармоники. СФ добавляет к каждой гармонике сигнала фазовый сдвиг 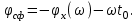 Добавка – φS устраняет разброс начальных фаз гармоник входного сигнала, добавка ωt0 сдвигает все гармоники на одно и то же время t0. Добавка – φS устраняет разброс начальных фаз гармоник входного сигнала, добавка ωt0 сдвигает все гармоники на одно и то же время t0.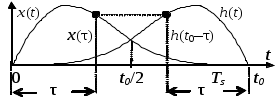 Фильтр, согласованный с прямоугольным импульсом 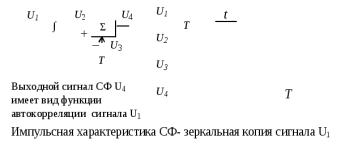 Фильтр, согласованный с радиоимпульсом 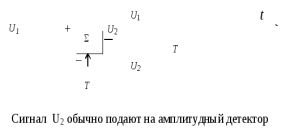 Согласованный фильтр как коррелятор  Система с двоичной фазовой модуляцией (2ФМ, BPSK) и когерентной демодуляцией  Требуется время на синхронизацию Восстановление несущей частоты в системе 2ФМ 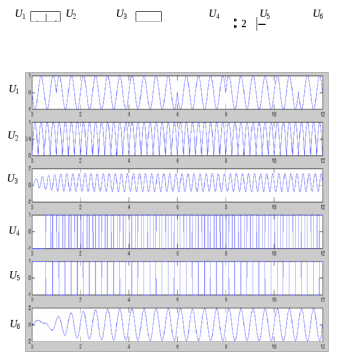 Требуется время на восстановление несущей частоты Восстановление тактовой частоты в системе 2ФМ 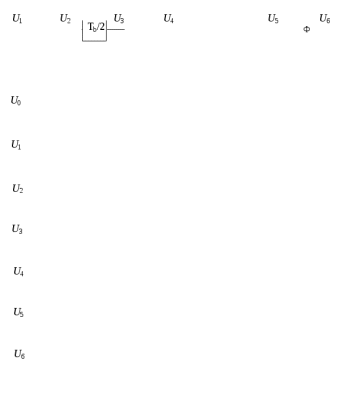 Требуется время на восстановление тактовой частоты Система 2ФМ с автокорреляционным демодулятором  Сигнал правильно детектируется после завершения синхронизации Сигнал правильно детектируется после завершения синхронизацииПри совпадении текущего бита с предыдущим U6 =1, при несовпадении U6 =–1 Система с квадратурной фазовой модуляцией (4ФМ, QPSK – quaternary phase shift keying) 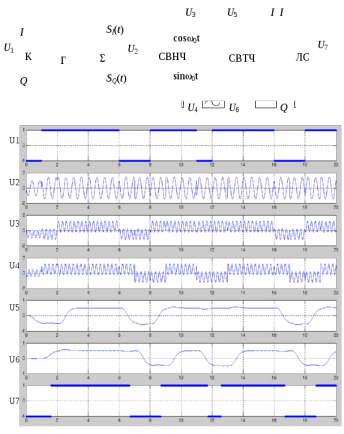 Разделение потока данных в системе с квадратурной манипуляцией  В системе со сдвигом меньше скачки фазы 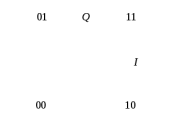 Автокорреляционный демодулятор системы 4ФМ 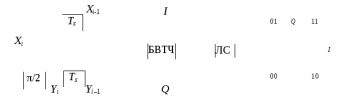 Векторное представление сигналов Xi, Yi Табл.1 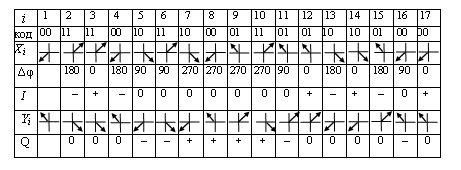 Δφ–разность фаз сигналов, представляющих текущий и предыдущий символы Табл.2  Сигналы I и Q принимают положительные, отрицательные или нулевые значения при перемножении идентичных, противоположных или ортогональных сигналов (XiXi-1, XiYi-1) соответственно. В зависимости от значений сигналов I и Q по табл. 2 определяется разность фаз Δφ, а по Δφ и предыдущему символу определяется текущий символ. Относительное (дифференциальное) кодирование Относительное кодирование применяется в системах с амплитудно-фазовой манипуляцией при когерентной и автокорреляционной демодуляции для уменьшения количества ошибок, вызванных неоднозначностью фазовой синхронизации опорного и принимаемого сигналов. Алгоритм относительного кодирования в системе 2ФМ:  Алгоритм относительного кодирования в системе 4ФМ:   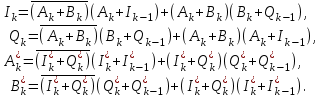 Коммутатор КМ в передатчике разделяет поток бит на четные и нечетные, коммутатор КМ в приемнике объединяет битовые потоки синфазного и квадратурного каналов. Частотная манипуляция (FSK) При М-ичной частотной манипуляции каждому символу соответствует своя частота передаваемого сигнала. Частоту изменяют: – перестройкой генератора, – переключением генераторов, – использованием синтезатора частоты. Сигналы различных частот могут быть ортогональными и не ортогональными, фаза – непрерывной или изменяющейся скачком на границе символов. Сигнал детектируют с использованием: – полосовых фильтров и амплитудных детекторов, – частотного детектора, определяющего разность частот, – процессора БПФ, определяющего частоту, – корреляционного приемника с разными опорными сигналами. Этот способ самый помехоустойчивый, сигналы должны быть ортогональными. Условие ортогональности сигналов разных частот: 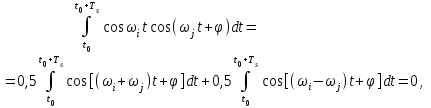 Первый интеграл от высокочастотного сигнала пренебрежимо мал. Значение второго интеграла зависит от to, Т и φ - фазы сигнала разностной частоты cos[(ωi – ωj)t+φ], показанного на рисунке, в момент начала интегрирования.  Этот интеграл обращается в 0 в следующих двух случаях: – длительность символа кратна периоду сигнала разностной частоты, интегрирование можно начинать в любой момент, демодуляция некогерентная. – длительность символа равна полупериоду сигнала разностной частоты, а момент начала интегрирования соответствующим образом синхронизован с принимаемым сигналом, демодуляция когерентная. Некогерентная демодуляция в системе с двоичной частотной манипуляцией (FSK –binary frequency shift keying), 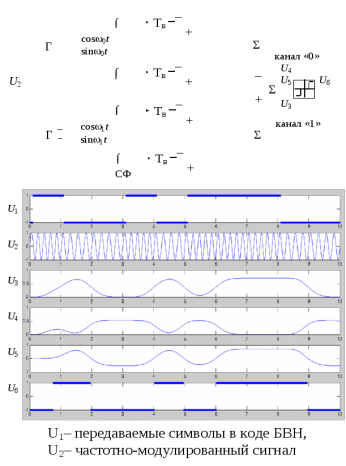 Частотная манипуляция с минимальным частотным сдвигом (MSK – minimum frequency shift keying) Модуляция MSK – – это двоичная частотная модуляция. Согласно тождеству 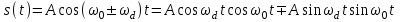 (1) (1)сигнал с двоичной частотной модуляцией можно получить в результате квадратурной модуляции, если прямоугольные модулирующие сигналы заменить гармоническими сигналами AI = Acosωdt и AQ = Asinωdt. Параметр ωd – девиация частоты, отклонение частоты от не модулированного значения ω0. Ортогональность сигналов, представляющих знаки 1 и 0, обеспечивается при минимальной разности частот Δf = 0,5/Tb (ωd = π Δf = 0,5 π/Tb), если детектирование когерентное. Подставив значение ωd в (1), получим 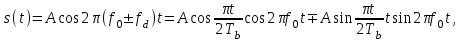 I =Acosωdt и Q =A sinωdt.– модулирующие сигналы. Частота и фаза сигнала MSK зависит от содержания двух соседних бит bI, bQ:
Модулятор системы с минимальным частотным сдвигом 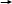      Tb 2Tb  Когерентная демодуляция сигналов с МЧС 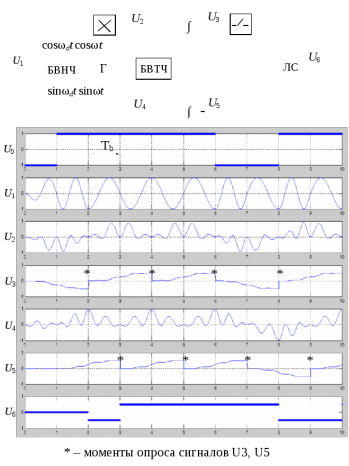 Оценка частотной полосы сигнала в системах BPSK, QPSK, MSK, FSK по ширине первого лепестка спектра  Сигнал MSK можно представить как две последовательности радиоимпульсов с разными несущими частотами. Спектры этих последовательностей показаны пунктиром. Вследствие интерференции гармоник частотная полоса становится уже (показана сплошной линией). Замена прямоугольных модулирующих импульсов (в системе QPSK) на синусоидальные (в системе MSK) расширяет основной лепесток спектра на 50%. В то же время уровень боковых лепестков в системе MSK, благодаря отсутствию скачков фазы, спадает с ростом частоты намного быстрее, чем у системы QPSK Модуляция с минимальным частотным сдвигом и гауссовой фильтрацией (GMSK) Гауссовый фильтр сглаживает фронты модулирующих импульсов, представляющих биты сообщения, придавая импульсам колоколообразную (гауссову) форму. Степень сглаживания зависит от отношения ширины полосы пропускания фильтра В, оцениваемой по уровню 0,7, к ширине полосы входного сигнала (1/T), т.е. от значения ВT. Значение ВТ выбирают с учетом требований к ширине спектра и допустимому уровню ошибок. В стандарте GSM ВТ = 0,3.  В отличие от систем с модуляцией QPSK, MSK сигналы AI и AQ взаимосвязаны Демодуляция может выполняться когерентным способом с восстановлением несущей, автокорреляционным способом или с использованием частотных дискриминаторов. В последнем случае требование к ортогональности сигналов, представляющих 1 и 0, отпадает. Индекс модуляции может выбираться в широком диапазоне (0,1…1). Модуляция OFDM (Orthogonal frequency division multiplex – частотное уплотнение с ортогональными несущими) Концептуальная схема модулятора OFDM 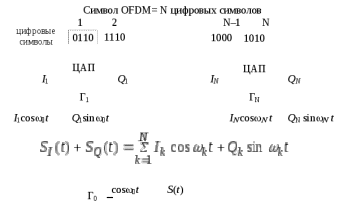 При модуляции ВЧ-колебания (ω0) нет удвоения ширины спектра Принцип реализации модуляции OFDM 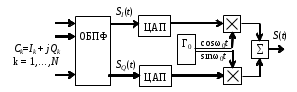 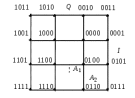 Принцип формирования сигналов OFDM   В алгоритмах БПФ размер массива данных кратен 2n. В системе цифрового телевидения используются массивы размерности N = 2048 (режим 2К) и N = 8192 (режим 8К). Допустимое количество несущих частот равно размерности массива. Для того чтобы между разными каналами был достаточный частотный интервал, количество несущих выбрано меньше допустимого: 1705 и 6817. Ширина полосы 7,61 МГц, модуляция QPSK, QAM-16, QAM – 64. Цифровое ТВ. Структура сигналов стандарта DVB-T 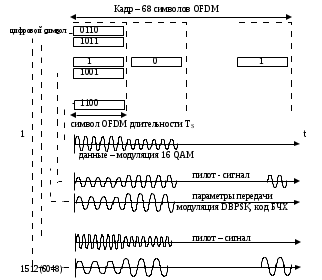 Число битов, передаваемых одной несущей, зависит от типа модуляции. На одной из несущих передаются параметры передачи – 68 битов в кадре: 1 бит – инициализация, 16 – синхронизация, 37– информация о типе модуляции, величине защитного интервала, скорости сверточного кода, номере кадра и т.д., 14 – проверка и исправление ошибки с использованием помехоустойчивого кода БЧХ и дифференциальной двоичной фазовой модуляции DBPSK Несущие синхронизуются пилот-сигналами, получаемыми модуляцией несущих псевдослучайной последовательностью. Пилот-сигналы распределены по частотам и по времени. Амплитуды и фазы пилот-сигналов известны в приемнике. Основные показатели эффективности цифровой системы связи Спектральная эффективность Rb/П – отношение скорости передачи (бит/c) к ширине полосы (Гц). Rb=log2M/Ts (M – объем алфавита символов, Ts – длительность символа), полоса П =1/Ts при амплитудно-фазовой манипуляции и П =M/Ts при частотной манипуляции, следовательно, спектральная эффективность: 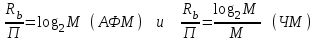 Удельные энергетические затраты Eb / N0 при заданной вероятности ошибки – отношение энергии Eb, затраченной на передачу одного бита, к односторонней спектральной плотности аддитивного белого гауссова шума N0. Вероятность битовой ошибки рb 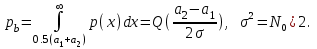 Функция Q табулирована, значение (a2 - a1)/(2 ) зависит от способа формирования сигнала. Чтобы сравнивать различные способы формирования сигналов по вероятности ошибок, безразмерную величину (a2 - a1)/(2 ) выражают через удельные энергетические затраты. 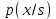 – вероятность принять сигнал х при переданном символе s. – вероятность принять сигнал х при переданном символе s. 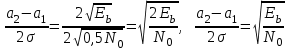 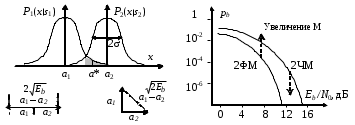 Максимальная пропускная способность канала Максимальной спектральной эффективностью Rbm/П = log2M обладает система с амплитудно-фазовой модуляцией. Максимальное значение Mмакс= (S+N)/N= 1+S/N – числу различимых, при наличии шума, градаций сигнала. Соотношение между максимально возможной спектральной эффективностью и энергетическими затратами дает теорема Шеннона – Хартли: максимальная скорость передачи информации Rbm (бит/с) по каналу с белым гауссовым шумом (пропускная способность канала) равна 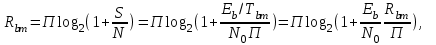 S и N – средняя мощность сигнала и шума, П – полоса пропускания. Минимально допустимое значение Eb/N0 можно найти при предельном переходе Rb/П→0: 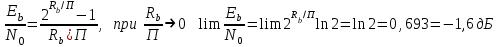 Значение Eb/N0 = 0,693 = -1,6 дБ называют пределом Шеннона. 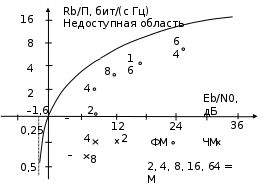 На рисунке указано соотношение параметров Rb/П и Eb/N0 при разных способах модуляции без помехоустойчивого кодирования (демодуляция сигналов с АФМ когерентная, ортогональных сигналов с ЧМ – некогерентная). Расширение спектра прямой последовательностью Расширение спектра прямой последовательностью – это модуляция сигнала двоичной псевдослучайной последовательностью (ПСП), выполняемая независимо от вида информационного сигнала. Такая модуляция может проводиться на разных этапах формирования сигнала. Исходная информационная последовательность данных суммируется с ПСП:  Расширение спектра прямой последовательностью на промежуточной частоте 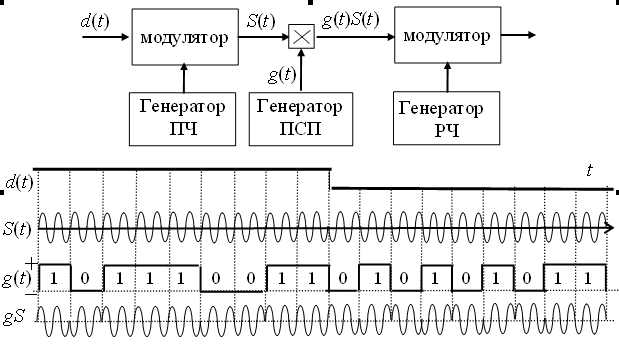 Расширение спектра S(f) сигнала и N(f) помехи  Преимущества систем с расширением спектра: - высокая помехоустойчивость, - конфиденциальность связи, - возможность многоканальной связи на одной несущей частоте, - возможность передачи маломощного сигнала, - высокая разрешающая способность по времени Расширение спектра скачкообразным изменением несущей частоты  Основные требования к ПСП - Непредсказуемость появления знаков 1 и 0, благодаря чему спектр сигнала становится равномерным, а определение алгоритма формирования ПСП по ее участку ограниченной длины – невозможным. - Наличие большого набора разных ПСП одинаковой длины для построения систем с кодовым разделением каналов. - Хорошие корреляционные свойства ПСП, описываемые функциями автокорреляции (ФАК) и взаимной корреляции (ФВК), периодическими и апериодическими. ФАК и ФВК вычисляются подсчетом разности числа совпадающих и не совпадающих разрядов сравниваемых ПСП при сдвигах одной из них. Периодические ФАК и ФВК вычисляются при циклическом сдвиге ПСП. Апериодические ФАК и ФВК вычисляются при обычном сдвиге ПСП (сравниваются части ПСП различной длины). Идеальной ФАК, периодической и апериодической, обладают только коды Баркера. Они существуют при N= 3, 4, 5, 7, 11 и 13. Это коды 6, D, 1D, 72, 712, 1F35 (в 16-ричном представлении). Пример вычисления корреляционных функций ПСП   Идеальные ФК Методы формирования ПСП М-последовательности – последовательности «максимальной» длины формируются сдвиговым регистром с суммирующей схемой в цепи обратной связи согласно алгоритму 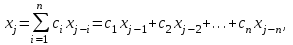 где хi – состояния разрядов регистра. Коэффициенты сi, принимающие значения 1 и 0, указывают номера разрядов регистра, подключенных к суммирующей схеме в цепи обратной связи. Суммирование выполняется по модулю 2. 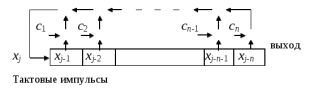 М-последовательности относятся к классу линейных ПСП. Комбинированные и каскадные ПСП формируются из нескольких линейных ПСП (например, последовательности Голда, Касами). Нелинейные ПСП формируются с использованием нелинейной логической функции в цепи обратной связи, или в результате нелинейного преобразования линейной ПСП. Примеры корреляционных функций m-последовательностей 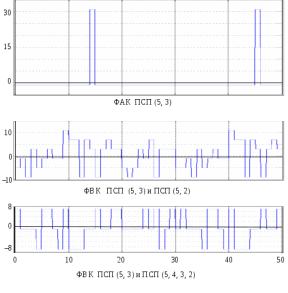 Синхронизация ПСП приемника и передатчика Синхронизация ПСП на этапе поиска (с точностью порядка 0,5 τэс) 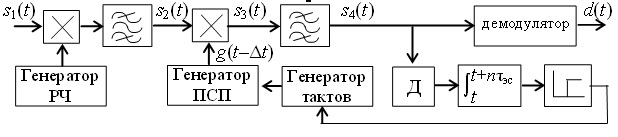 Принимаемый сигнал промежуточной частотыs2(t)=d(t)g(t)cos(ωt – φ) Если Δt < τэс, то s4(t) ≈d(t)cos(ωt – φ) Точная синхронизация 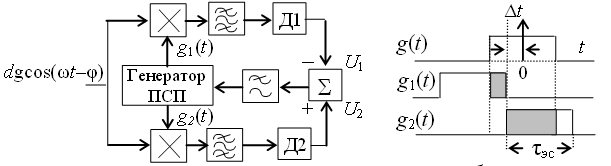 Полоса пропускания ФНЧ определяет длительность интервала времени, на котором оценивается корреляция рассматриваемых сигналов. Чем больше этот интервал, тем меньше влияние шума и разброса границ элементарных символов ПСП на точность синхронизации. Фильтр, согласованный с ПСП Баркера  Порядок установки инверторов, определяющий импульсную характеристику фильтра, является зеркальным отражением осциллограммы входного сигнала. СФИ – фильтр, согласованный с прямоугольным импульсом. |
