Лр 100 физика. LR100_Логвин_Александр. Диапазон мех секундомера
 Скачать 193.33 Kb. Скачать 193.33 Kb.
|
|
Среднее арифметическое | Сумма (с учетом знаков) отклонений от среднего арифметического | Сумма квадратов отклонений от среднего арифметического | |
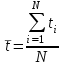 =4,98 =4,98 | 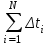 =0 =0 | 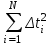 =313,735 =313,735 |
| № | ячеек гистограммы 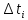 , c , c | число наблюдений в ячейке, 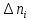 | 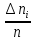 |
| 1 | 4,6-4,7 | 1 | 0,015873 |
| 2 | 4,7-4,8 | 5 | 0,079365 |
| 3 | 4,8-4,9 | 8 | 0,126984 |
| 4 | 4,9-5,0 | 19 | 0,301587 |
| 5 | 5,0-5,1 | 15 | 0,238095 |
| 6 | 5,1-5,2 | 11 | 0,174603 |
| 7 | 5,2-5,3 | 3 | 0,047619 |
| 8 | 5,3-5,4 | 1 | 0,015873 |
Пример для 1-ой строки:
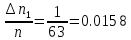
Строим гистограмму экспериментальных значений и кривую закона распределения (рис. 2):
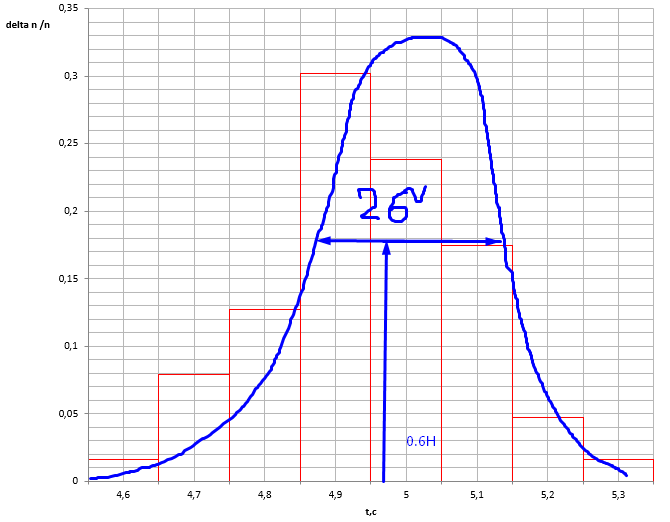
Рис.2. Гистограмма экспериментальных значений (Δn) и кривая закона распределения (Δn/n).
На уровне 0.6 от максимального значения находим ширину кривой закона распределения:
2
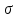
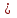 0,32
0,32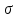 =
=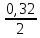
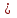 0,16 с
0,16 сВывод:
В данной лабораторной работе был освоен алгоритм обработки результатов прямых многократных измерений, построена гистограмма экспериментальных значений определяемой величины и оценены параметры распределения Гаусса по кривой закона распределения.
Было получено:
t=(4,98±0.04) c P=0.9.
среднеквадратичная погрешность отдельного результата измерения примерно совпадает со среднеквадратичным отклонением, найденным из графика.
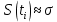
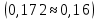
Из графика 1 можно сделать вывод об отсутствии дрейфа, свидетельством этого является то, что результаты наблюдений не увеличиваются систематически с течением времени.
Контрольные вопросы:
1. Если значение физической величины находят непосредственным отсчетом по шкале прибора, то такие измерения называются прямыми
При косвенных измерениях результат. определяется по формулам на основе результатов прямых измерений других величин.
Невоспроизводимые косвенные измерения - когда невозможно повторить наблюдения в тождественных условиях .
2.

3. Потому что при разных доверительных вероятностях будут получаться разные результаты
4. Это означает, что с вероятностью в 0,68 значение не выйдет за пределы доверительного интервала
5. Систематическая - Это погрешность, изменяющаяся во времени по определённому закону
Случайная погрешность - Это составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины,
проведенных в одних и тех же условиях.
Приборной погрешностью - случайная ошибка, обусловленная измерительными приборами и приспособлениями
6. Гистогра́мма — способ представления табличных данных в графическом виде — в виде столбчатой диаграммы.
Закон распределения - это закон, описывающий область значений случайной величины и соответствующие вероятности появления этих значений.

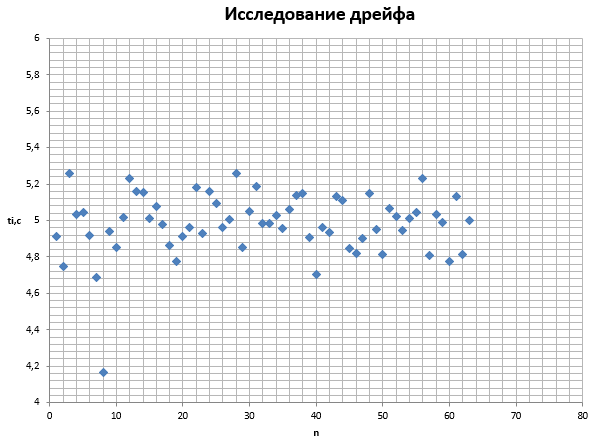
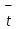 =
=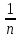
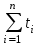 = 313,735/ 63= 4,98 c
= 313,735/ 63= 4,98 c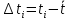 .
.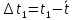 = 4,913– 4,98= -0,067 c
= 4,913– 4,98= -0,067 c
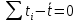
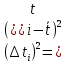 и сумму
и сумму 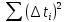 , заносим результаты в таб.:
, заносим результаты в таб.: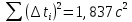
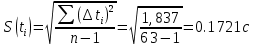
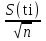 =0,1721/
=0,1721/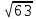 = 0,0217 с
= 0,0217 с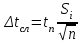 = tn*S(
= tn*S(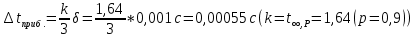
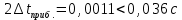
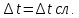
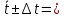 4,98±0,04 с (с вероятностью P=0, 90);
4,98±0,04 с (с вероятностью P=0, 90);