Ответы на задание 4. Дифференциал функции
 Скачать 219 Kb. Скачать 219 Kb.
|
|
Дифференциал функции. Пусть функция y = f(x) имеет производную в точке х: Тогда можно записать: Следовательно: Величина x- бесконечно малая более высокого порядка, чем f(x)x, т.е. f(x)x- главная часть приращения у. Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x). Из определения следует, что dy = f(x)x или dy = f(x)dx. Можно также записать: Геометрический смысл дифференциала.  y yf(x) K dy M y L x x + x x Из треугольника MKL: KL = dy = tgx = yx Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке. Свойства дифференциала. Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства: d(u v) = (u v)dx = udx vdx = du dv d(uv) = (uv)dx = (uv + vu)dx = vdu + udv d(Cu) = Cdu Дифференциал сложной функции. Инвариантная форма записи дифференциала. Пусть y = f(x), x = g(t), т.е у- сложная функция. Тогда dy = f(x)g(t)dt = f(x)dx. Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала. Однако, если х- независимая переменная, то dx = x, но если х зависит от t, то х dx. Таким образом форма записи dy = f(x)x не является инвариантной. Пример. Найти производную функции Сначала преобразуем данную функцию: Пример. Найти производную функции  Пример. Найти производную функции 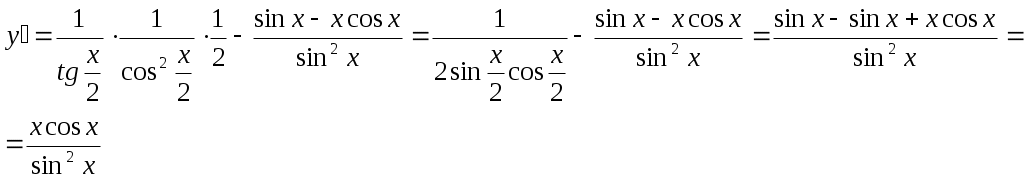 Пример. Найти производную функции 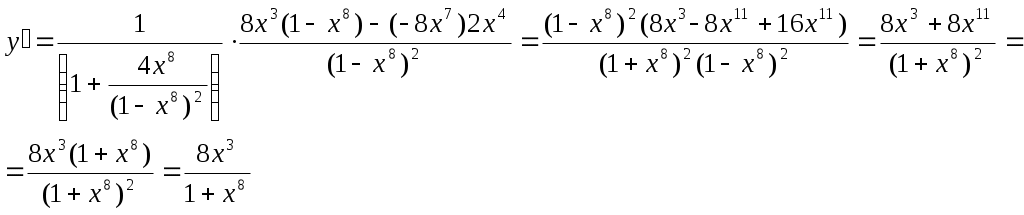 Пример. Найти производную функции  Приложение производной Применение дифференциала к приближенным вычислениям. Дифференциал функции y = f(x) зависит от х и является главной частью приращения х. Также можно воспользоваться формулой Тогда абсолютная погрешность Относительная погрешность Более подробно применение дифференциала к приближенным вычислениям будет описано ниже. При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая производит разложение любой функции в ряды Тейлора и Маклорена, а также вычисляет значение функции в заданной точке, выводит погрешность вычислений. Теоремы о среднем. Теорема Ролля. (Ролль (1652-1719)- французский математик) Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка , a < < b, в которой производная функция f(x) равная нулю, f() = 0. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки. Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M m. Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за можно принять любую точку интервала. Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим , a < < b точку, в которой f() = M. Так как М- наибольшее значение функции, то для любого х ( будем считать, что точка + х находится внутри рассматриваемого интервала) верно неравенство: f() = f( + x) – f() 0 При этом Но так как по условию производная в точке существует, то существует и предел Т.к. 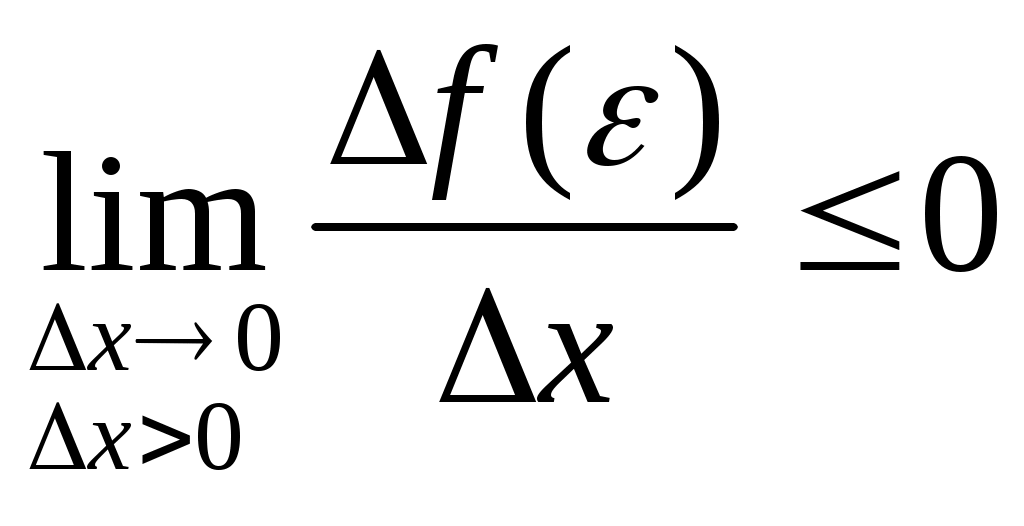 и и 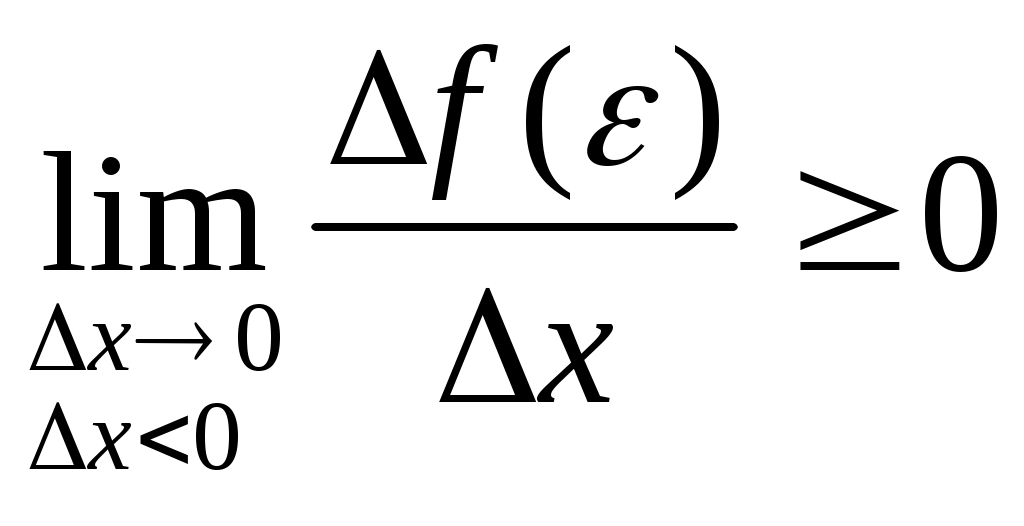 , то можно сделать вывод: , то можно сделать вывод:Теорема доказана. Теорема Ролля имеет несколько следствий: Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем f(a) = f(b) = = 0, то существует по крайней мере одна точка , a < < b, такая, что f() = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю. Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю. Теорема Лагранжа. (Жозеф Луи Лагранж (1736-1813) французский математик) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка a < < b, такая, что Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке. Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа. Отношение 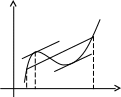 у уВ А 0 а b x Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно. Доказательство. Рассмотрим некоторую вспомогательную функцию F(x) = f(x) – yсек АВ Уравнение секущей АВ можно записать в виде:  Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка , a < < b, такая что F() = 0. Т.к. Теорема доказана.  Определение. Выражение Определение. Выражение В дальнейшем эта формула будет очень часто применяться для доказательства самых разных теорем. Иногда формулу Лагранжа записывают в несколько другом виде: где 0 < < 1, x = b – a, y = f(b) – f(a). Теорема Коши. ( Коши (1789-1857)- французский математик) Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка , a < < b, такая, что Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке . Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это- очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы. Доказательство. Рассмотрим вспомогательную функцию которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка , a < < b, такая, что F() = 0. Т.к. А т.к. Теорема доказана. Следует отметить, что рассмотренная выше теорема Лагранжа является частным случаем (при g(x) = x) теоремы Коши. Доказанная нами теорема Коши очень широко используется для раскрытия так называемых неопределенностей. Применение полученных результатов позволяет существенно упростить процесс вычисления пределов функций, что будет подробно рассмотрено ниже. Раскрытие неопределенностей. Правило Лопиталя. (Лопиталь (1661-1704) – французский математик) К разряду неопределенностей принято относить следующие соотношения: Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при ха равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует. Доказательство. Применив формулу Коши, получим: где - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0: Пусть при ха отношение Теорема доказана. Пример: Найти предел Как видно, при попытке непосредственного вычисления предела получается неопределенность вида f (x) = 2x +  ; ;Пример: Найти предел  . . . .Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя. Пример: Найти предел  . .  Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.). Пример: Найти предел Неопределенности вида Пример: Найти предел 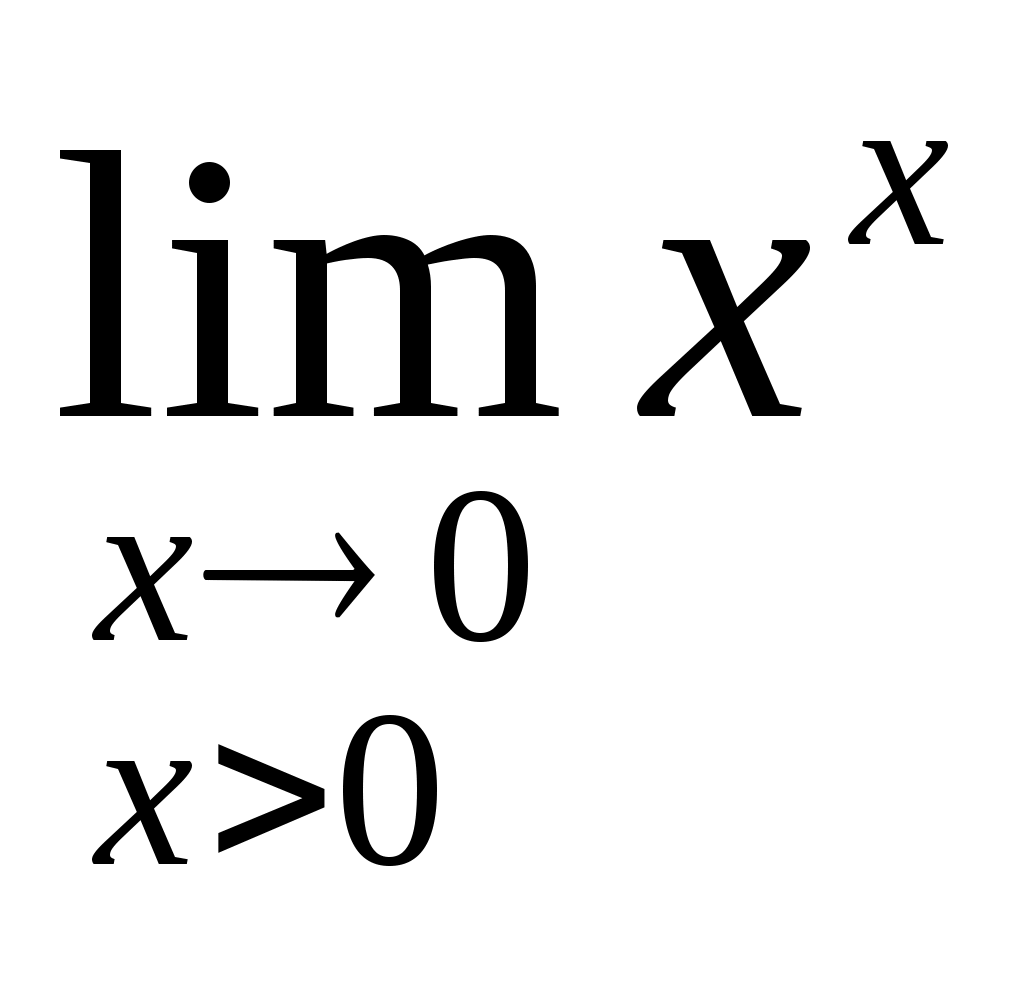 . .Здесь y = xx, lny = xlnx. Тогда  . Следовательно . Следовательно Пример: Найти предел Производные и дифференциалы высших порядков. Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную Если найти производную функции f(x), получим вторую производную функции f(x). т.е. y = (y) или Этот процесс можно продолжить и далее, находя производные степени n.  . .Общие правила нахождения высших производных. Если функции u = f(x) и v = g(x) дифференцируемы, то (Сu)(n) = Cu(n); (u v)(n) = u(n) v(n); 3) Это выражение называется формулой Лейбница. Также по формуле dny = f(n)(x)dxn может быть найден дифференциал n- го порядка.  |
