Дифференциальные-уравнения-1го-порядка. Дифференциальные уравнения. Основные понятия об обыкновенных дифференциальных уравнениях. Определение 1
 Скачать 462.5 Kb. Скачать 462.5 Kb.
|
|
Дифференциальные уравнения. § 1. Основные понятия об обыкновенных дифференциальных уравнениях. Определение 1. Обыкновенным дифференциальным уравнением n – го порядка для функции yаргументаxназывается соотношение вида где F– заданная функция своих аргументов. В названии этого класса математических уравнений термин «дифференциальное» подчеркивает, что в них входят производные Обыкновенное дифференциальное уравнение может не содержать в явном виде аргумент x, искомую функцию а) б) При написании обыкновенных дифференциальных уравнений часто используются обозначения производных через дифференциалы: в) г) образующее после деления на dx эквивалентную форму задания уравнения: Функция Например, уравнение 3-го порядка Найти тем или иным приемом, например, подбором, одну функцию, удовлетворяющую уравнению, не означает решить его. Решить обыкновенное дифференциальное уравнение – значит найти все функции, образующие при подстановке в уравнение тождество. Для уравнения (1.1) семейство таких функций образуется с помощью произвольных постоянных и называется общим решением обыкновенного дифференциального уравнения n-го порядка, причем число констант совпадает с порядком уравнения: Например, общим решением дифференциального уравнения Задавая некоторые допустимые значения всем произвольным постоянным в общем решении или в общем интеграле, получаем определенную функцию, уже не содержащую произвольных констант. Эта функция называется частным решением или частным интегралом уравнения (1.1). Для отыскания значений произвольных постоянных, а следовательно, и частного решения, используются различные дополнительные условия к уравнению (1.1). Например, могут быть заданы так называемые начальные условия при В правых частях начальных условий (1.2) заданы числовые значения функции и производных, причем, общее число начальных условий равно числу определяемых произвольных констант. Задача отыскания частного решения уравнения (1.1) по начальным условиям называется задачей Коши. § 2. Обыкновенные дифференциальные уравнения 1-го порядка – основные понятия. Обыкновенное дифференциальное уравнение 1-го порядка (n=1) имеет вид: Теорема 2.1. Если в уравнении Геометрически общее решение уравнения 1-го порядка представляет собой семейство кривых на плоскости XOY, не имеющих общих точек и отличающихся друг от друга одним параметром – значением константы C. Эти кривые называются интегральными кривыми для данного уравнения. Интегральные кривые уравнения 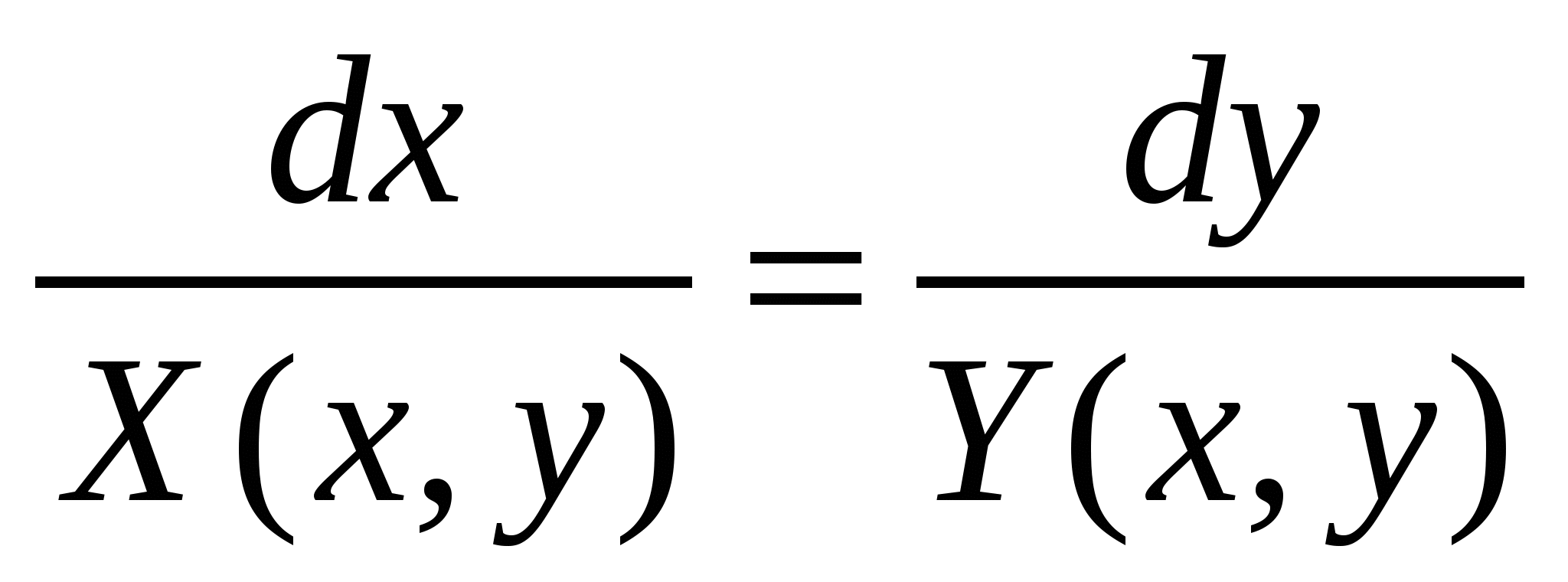 . .§ 3. Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида или уравнение вида Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия: Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решениеy=a, то y=a тоже будет решением уравнения (3.1). Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение Интегральные кривые (3.3) будут дополнены решениями Пример. Решить уравнение: Решение. Разделяем переменные: Интегрируя, получаем Далее из уравнений § 4. Однородные дифференциальные уравнения 1-го порядка. Определение 1. Уравнение 1-го порядка Пример 1. Показать, что функция Решение. что и требовалось доказать. Теорема. Любая функция Доказательство. Первое утверждение теоремы очевидно, т.к. Определение 2. Уравнение в котором Mи N– однородные функции одной и той же степени, т.е. обладают свойством Очевидно, что это уравнение всегда может быть приведено к виду Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, гдеz(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: Интегрируя, получаем общий интеграл уравнения относительно функции z(x) 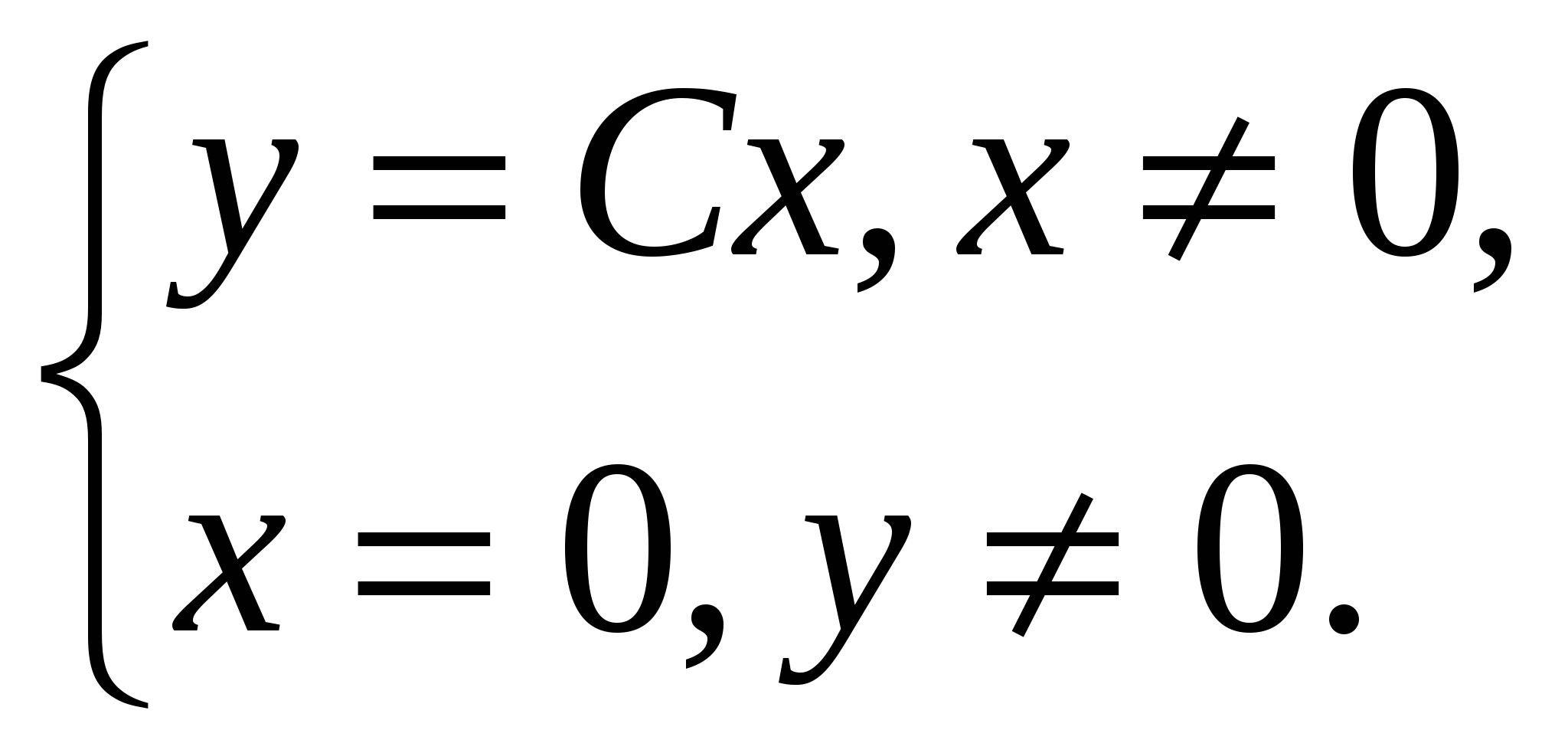 . .Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy. § 5. Дифференциальные уравнения, приводящиеся к однородным. Рассмотрим уравнение вида Если 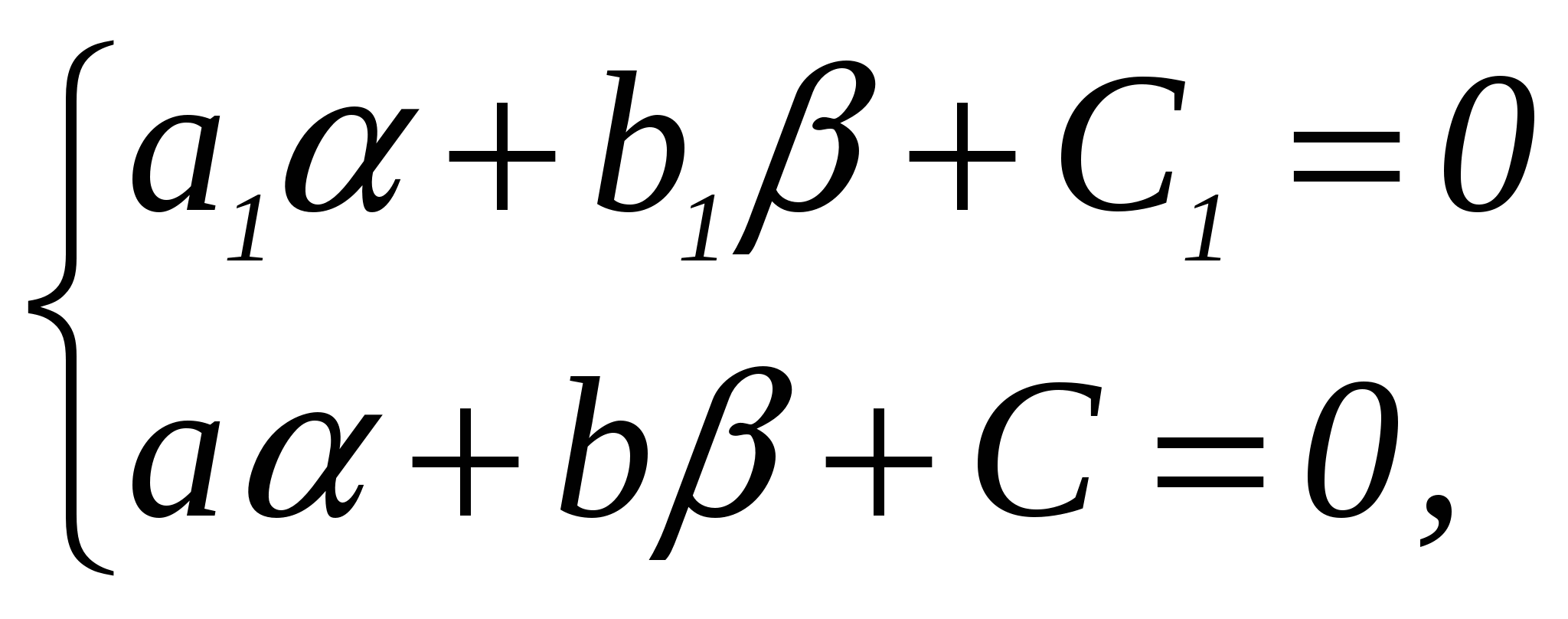 Приводится к однородному уравнению Если Полагая z=ax+by, приходим к уравнению, не содержащему независимой переменной. Рассмотрим примеры. Пример 1. Проинтегрировать уравнение и выделить интегральную кривую, проходящую через точки: а) (2;2); б) (1;-1). Решение. Положим y=zx. Тогда dy=xdz+zdxи Сократим на Разделим переменные: Интегрируя, получим или Заменив здесь z на Это семейство окружностей Теперь режим задачи Коши: А) полагая в общем интеграле x=2, y=2, находим С=2, поэтому искомым решением будет Б) ни одна из окружностей (5.2) не проходит через точку (1;-1). Зато полупрямая y = -x, Пример 2. Решить уравнение: Решение. Уравнение является частным случаем уравнения (5.1). Определитель 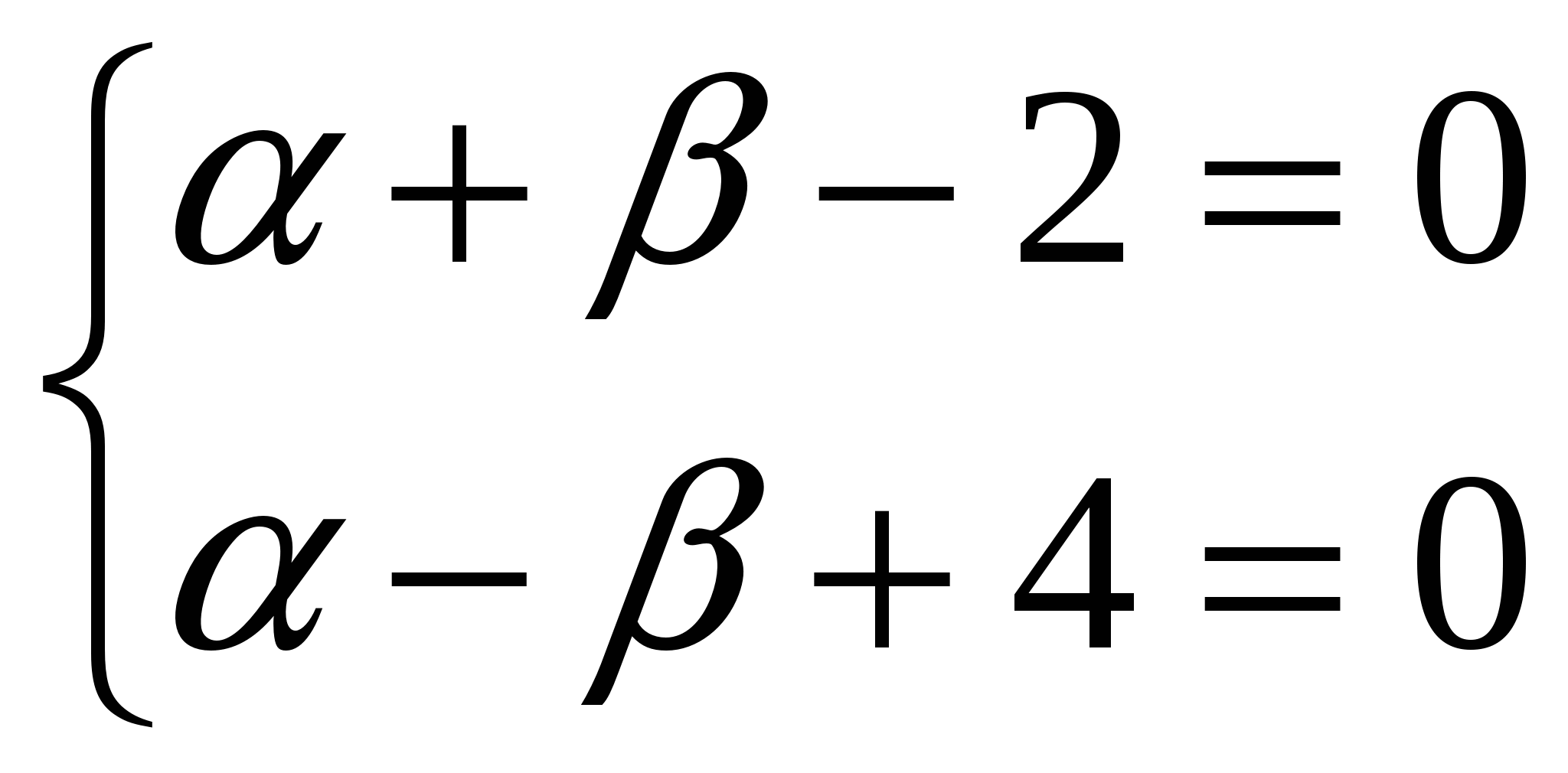 Решая, получим, что Возвращаясь к старым переменным xиyпо формулам § 6. Обобщенное однородное уравнение. Уравнение M(x,y)dx+N(x,y)dy=0 называется обобщенным однородным, если удается подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени mотносительно x, y, dxи dyпри условии, что xсчитается величиной первого измерения, y – kго измерения, dxи dy – соответственно нулевого и (k-1)-го измерений. Например, таким будет уравнение Действительно при сделанном предположении относительно измерений x, y, dxи dyчлены левой части Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки Интегрируя его, находим § 7. Линейные дифференциальные уравнения 1-го порядка. Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид: где P(x) и Q(x) – заданные непрерывные функции от x. Если функция и называется линейным однородным уравнением, в противном случае Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными: Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(x) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(x) так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим: Подставляя найденную производную в уравнение (7.1), будем иметь: или Откуда Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) за скобку: 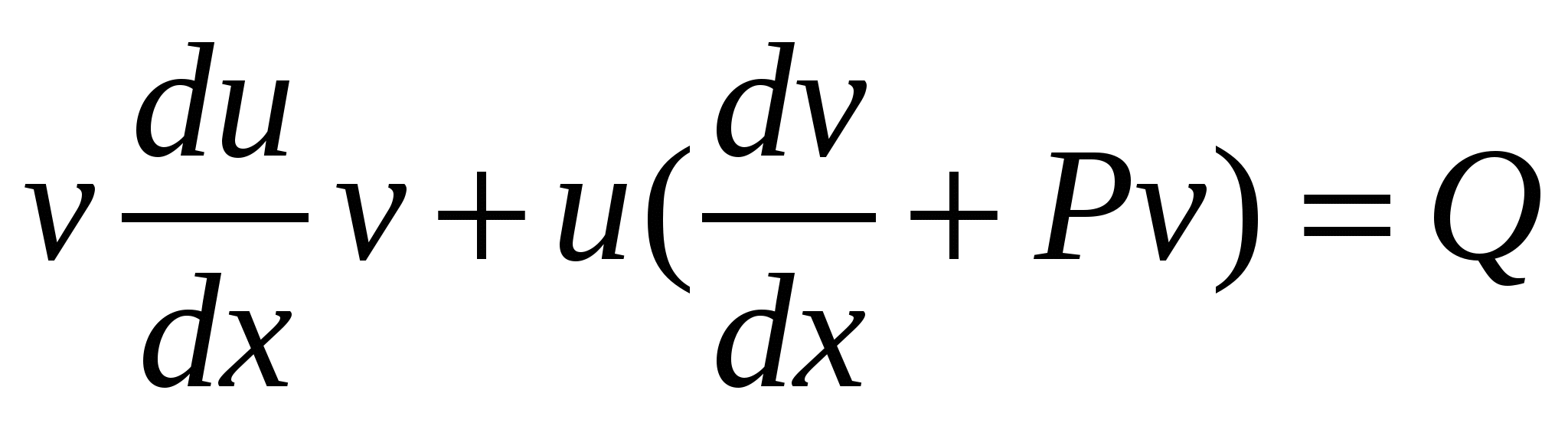 (7.5) (7.5)Потребуем обращения в нуль круглой скобки: 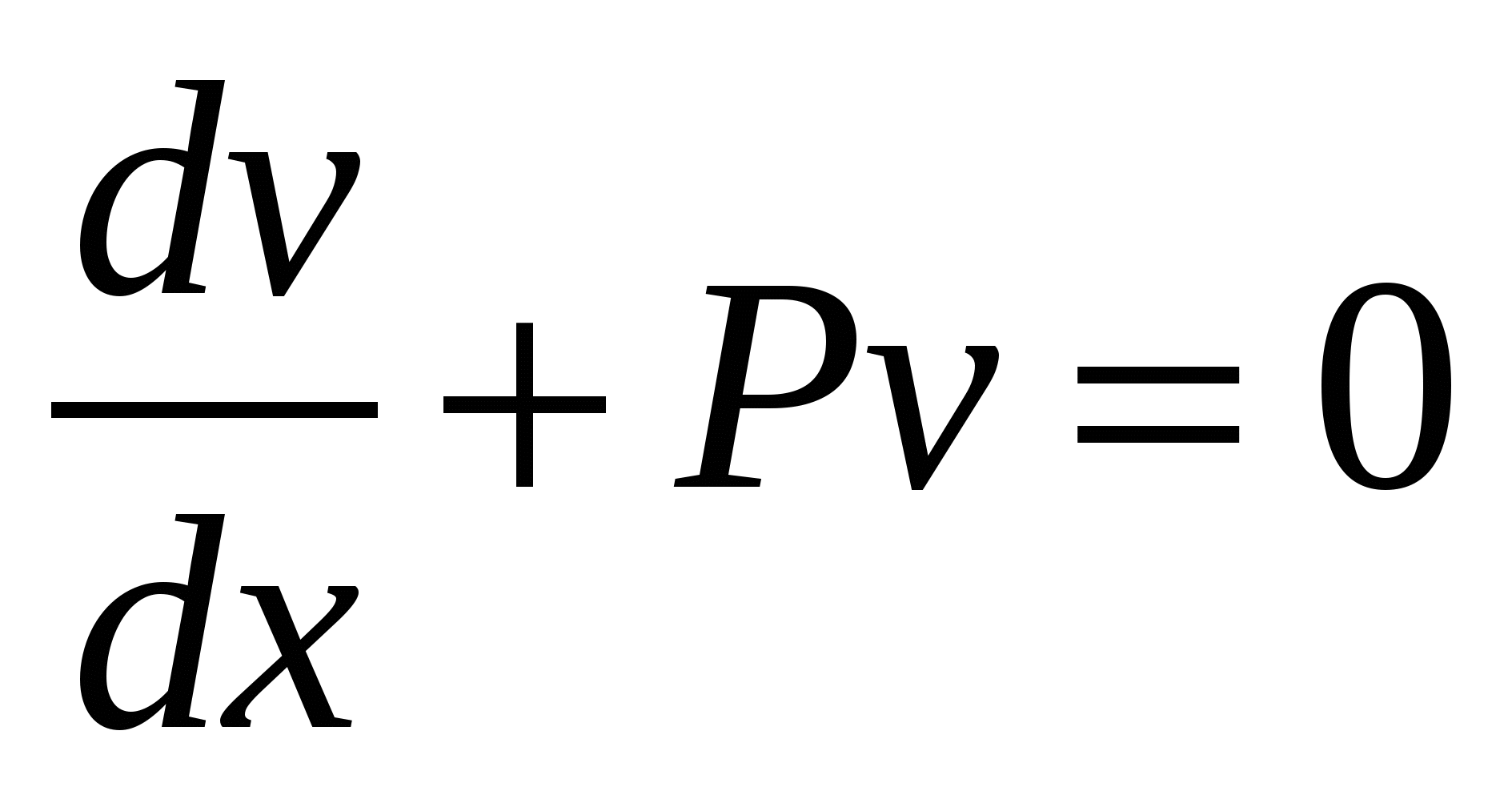 . .Решим это уравнение, полагая произвольную постоянную C равной нулю: 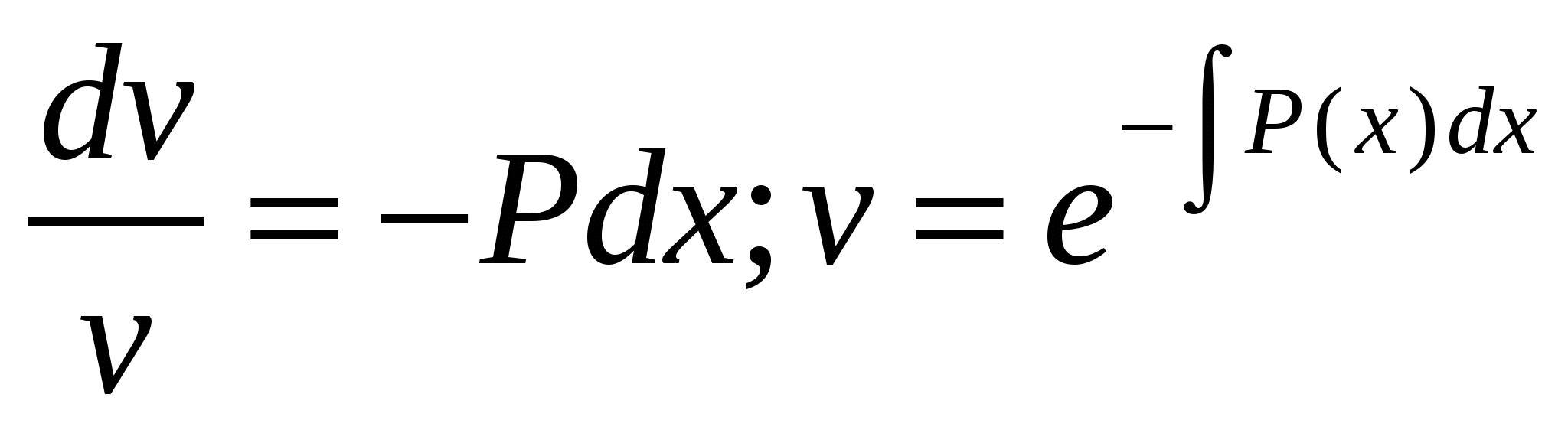 . С найденной функцией v(x) вернемся в уравнение (7.5): . С найденной функцией v(x) вернемся в уравнение (7.5): Решая его, получим: Следовательно, общее решение уравнения (7.1) имеет вид: § 8. Уравнение Бернулли. Определение. Дифференциальное уравнение вида Предполагая, что Введем новую функцию Пример. Найти общее решение уравнения: Решение. Уравнение (8.2) является уравнением Бернулли, причем Будем искать решение уравнения в виде Тогда В левой части последнего уравнения сгруппируем второе и третье слагаемые, которые содержат функцию u(x), и потребуем, чтобы которое является уравнением с разделяющимися переменными для функции u(x). Решим его 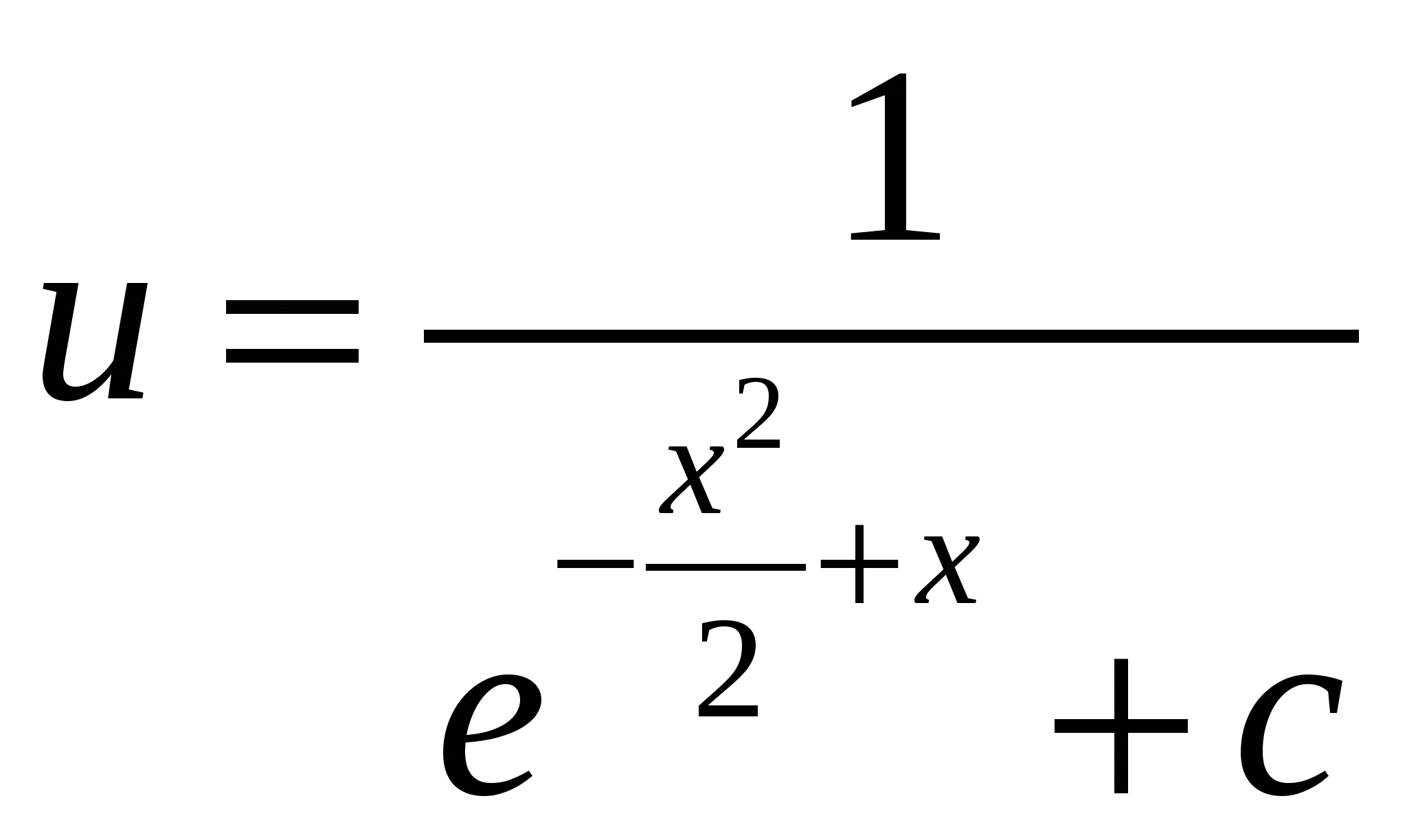 Следовательно, общее решение данного уравнения имеет вид: 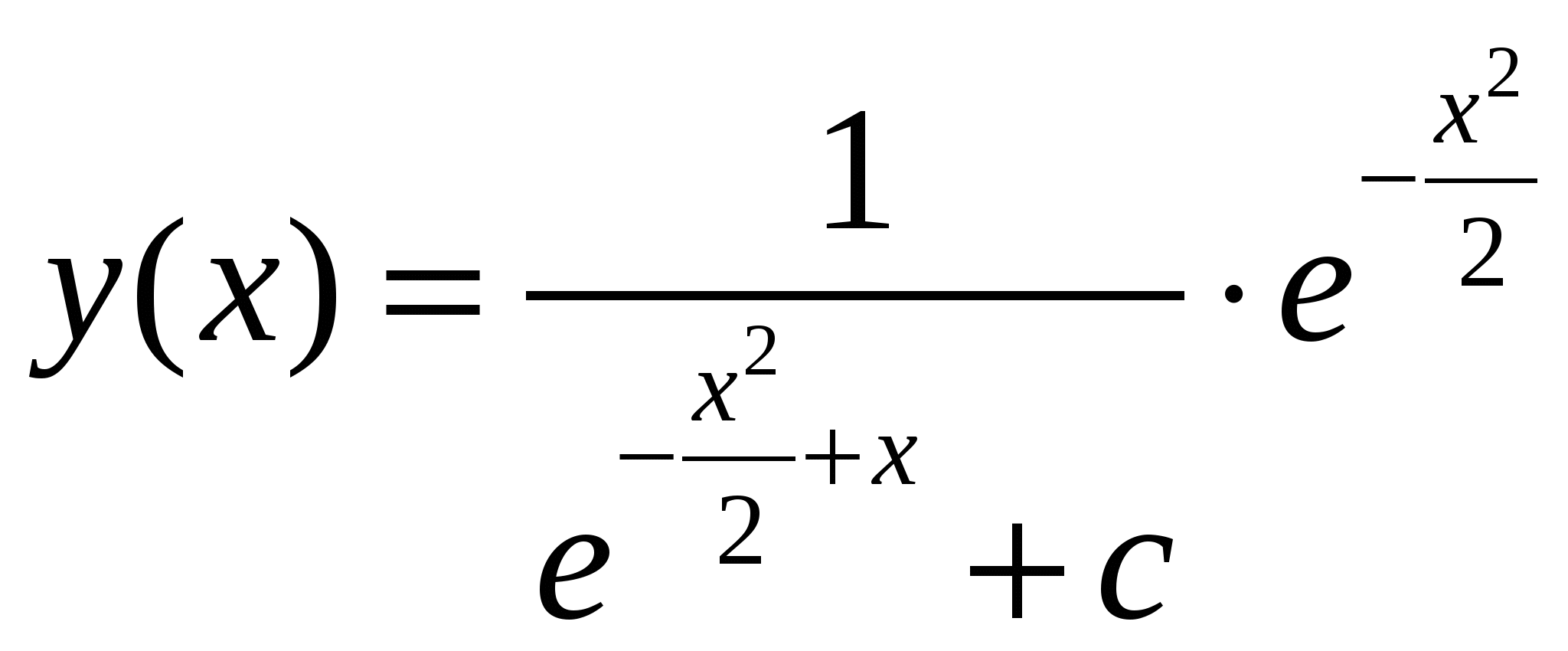 , y(x)=0. , y(x)=0.§ 9. Дифференциальные уравнения в полных дифференциалах. Определение. Если в уравнении M(x,y)dx+N(x,y)dy=0 (9.1) левая часть есть полный дифференциал некоторой функции U(x,y), то оно называется уравнением в полных дифференциалах. Это уравнение можно переписать в виде du(x,y)=0, следовательно, его общий интеграл есть u(x,y)=c. Например, уравнение xdy+ydx=0 есть уравнение в полных дифференциалах, так как его можно переписать в виде d(xy)=0. Общим интегралом будет xy=c. Теорема. Предположим, что функции M и Nопределены и непрерывны в некоторой односвязной областиDи имеют в ней непрерывные частные производные соответственно по yи поx. Тогда, для того, чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество Доказательство. Доказательство необходимости этого условия очевидно. Поэтому докажем достаточность условия (9.2). Покажем, что может быть найдена такая функция u(x,y), что Действительно, поскольку 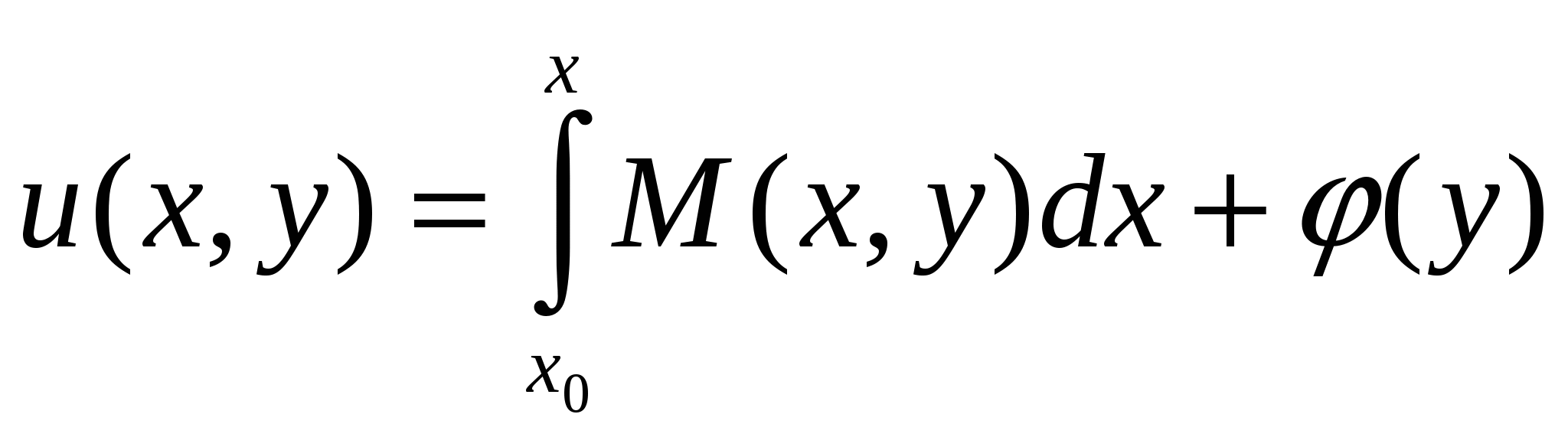 (9.3) , где (9.3) , где 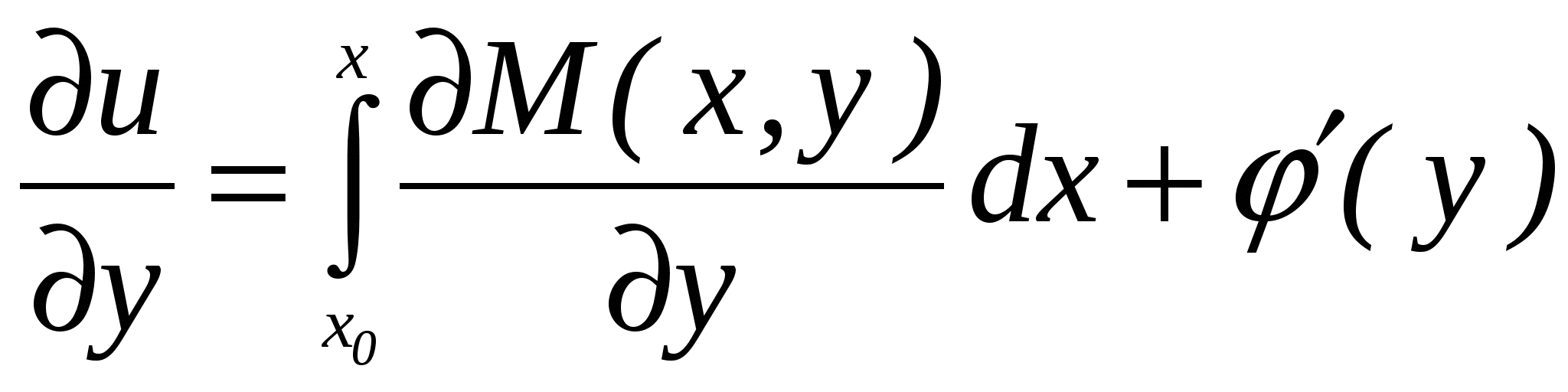 . Но . Но 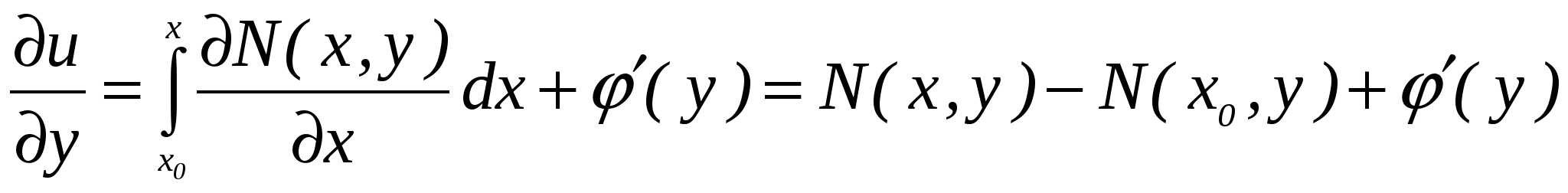 . .Положим 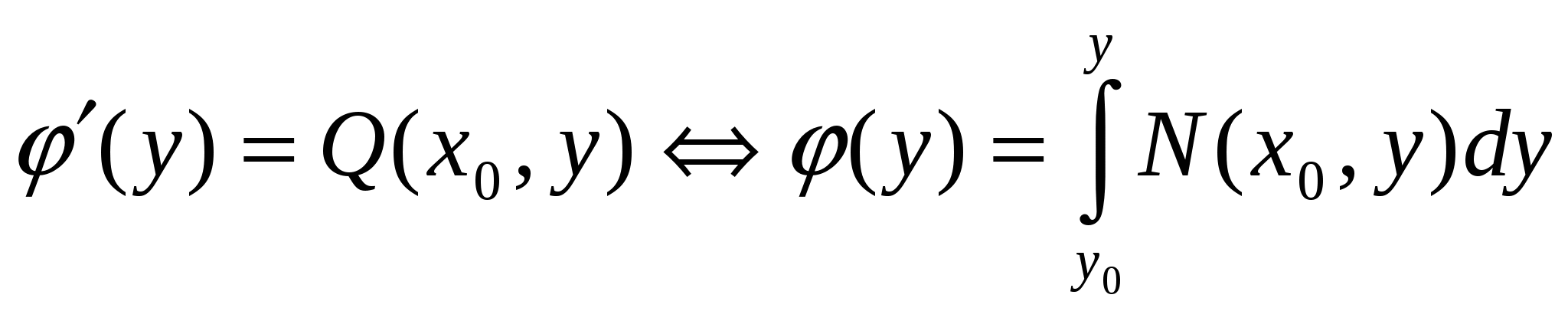 и тогда и тогда Итак, построена функция 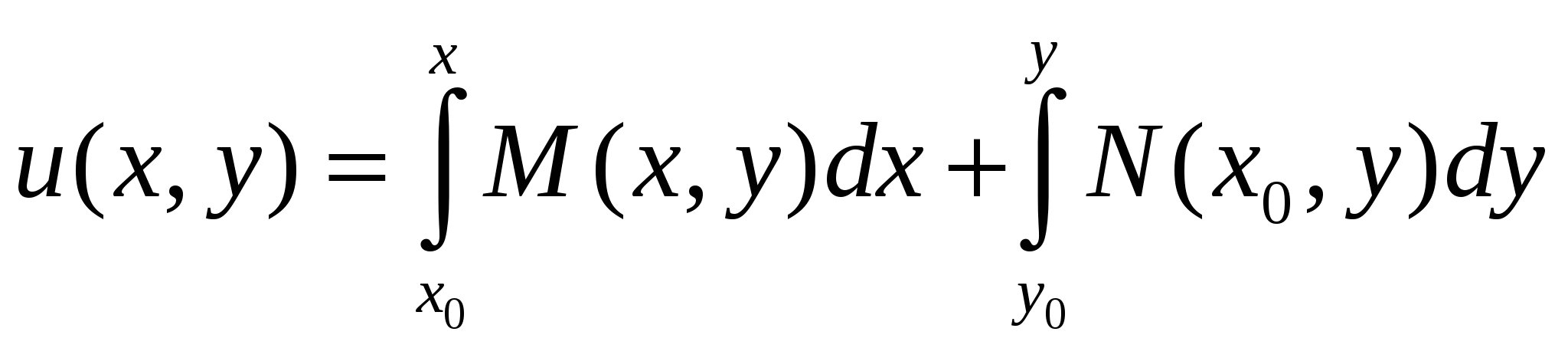 , для которой , для которой Рассмотрим пример. Пример. Найти общий интеграл уравнения: Решение. Здесь Тогда Теперь продифференцируем u(x,y) по y и приравняем полученное в результате выражение выписанной выше частной производной Откуда § 10. Интегрирующий множитель. Если уравнение M(x,y)dx + N(x,y)dy = 0 не является уравнением в полных дифференциалах и существует функция µ = µ(x,y), такая что после умножения на нее обеих частей уравнения получается уравнение µ(Mdx + Ndy) = 0 в полных дифференциалах, т. е. µ(Mdx + Ndy)du, то функция µ(x,y) называется интегрирующим множителем уравнения. В случае, когда уравнение уже есть уравнение в полных дифференциалах, полагают µ = 1. Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах. Если µ есть непрерывно дифференцируемая функция от x и y, то Отсюда следует, что интегрирующий множитель µ удовлетворяет следующему уравнению с частными производными 1-го порядка: Если заранее известно, что µ= µ(ω), где ω – заданная функция от x и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µ от независимой переменной ω: где 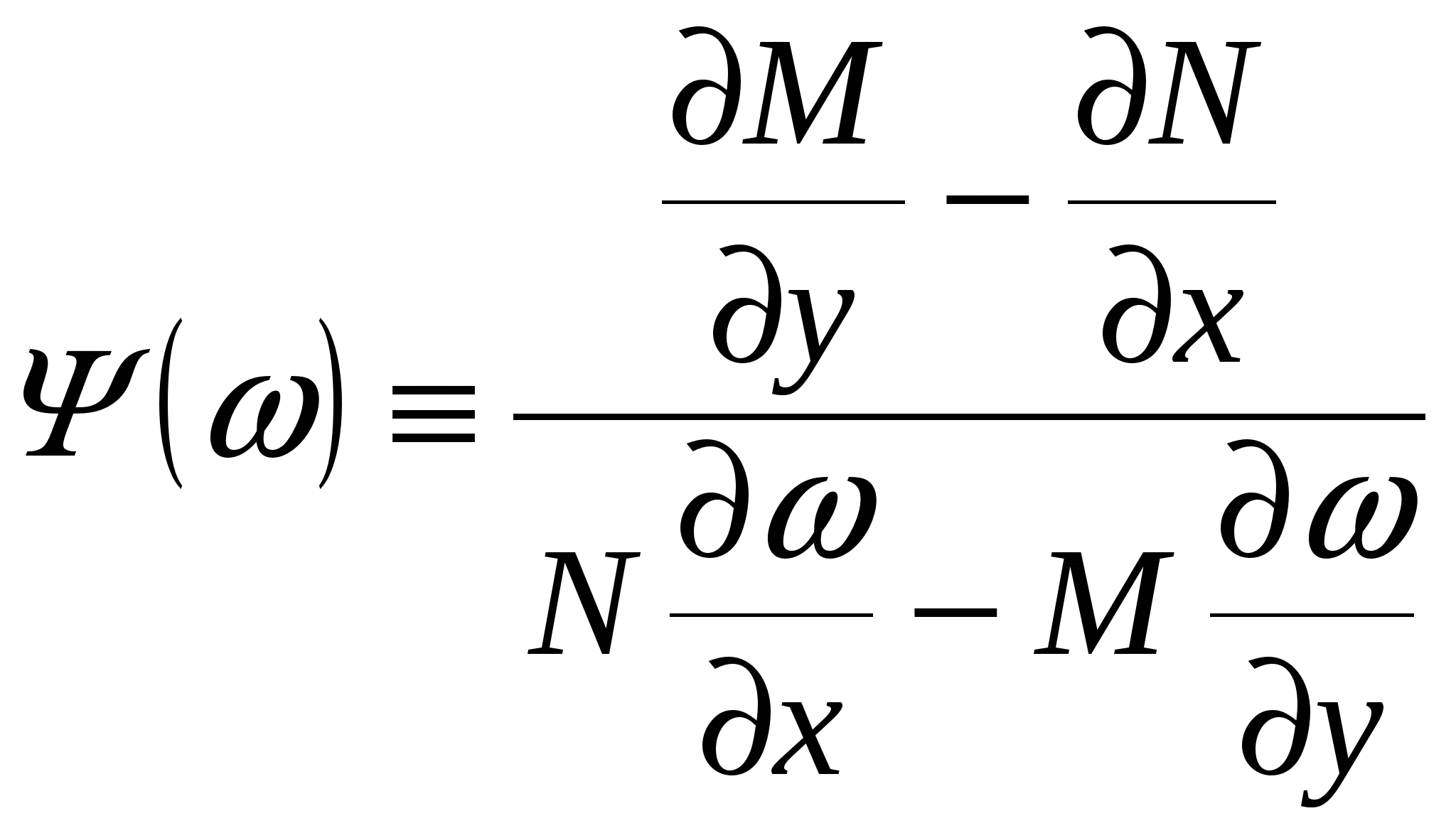 , т. е. дробь является функцией только от ω. , т. е. дробь является функцией только от ω.Решая уравнение (10.2), находим интегрирующий множитель В частности уравнение M(x,y)dx + N(x,y)dy = 0 имеет интегрирующий множитель, зависящий только от x(ω = x) или только от y(ω = y), если выполнены соответственно следующие условия: 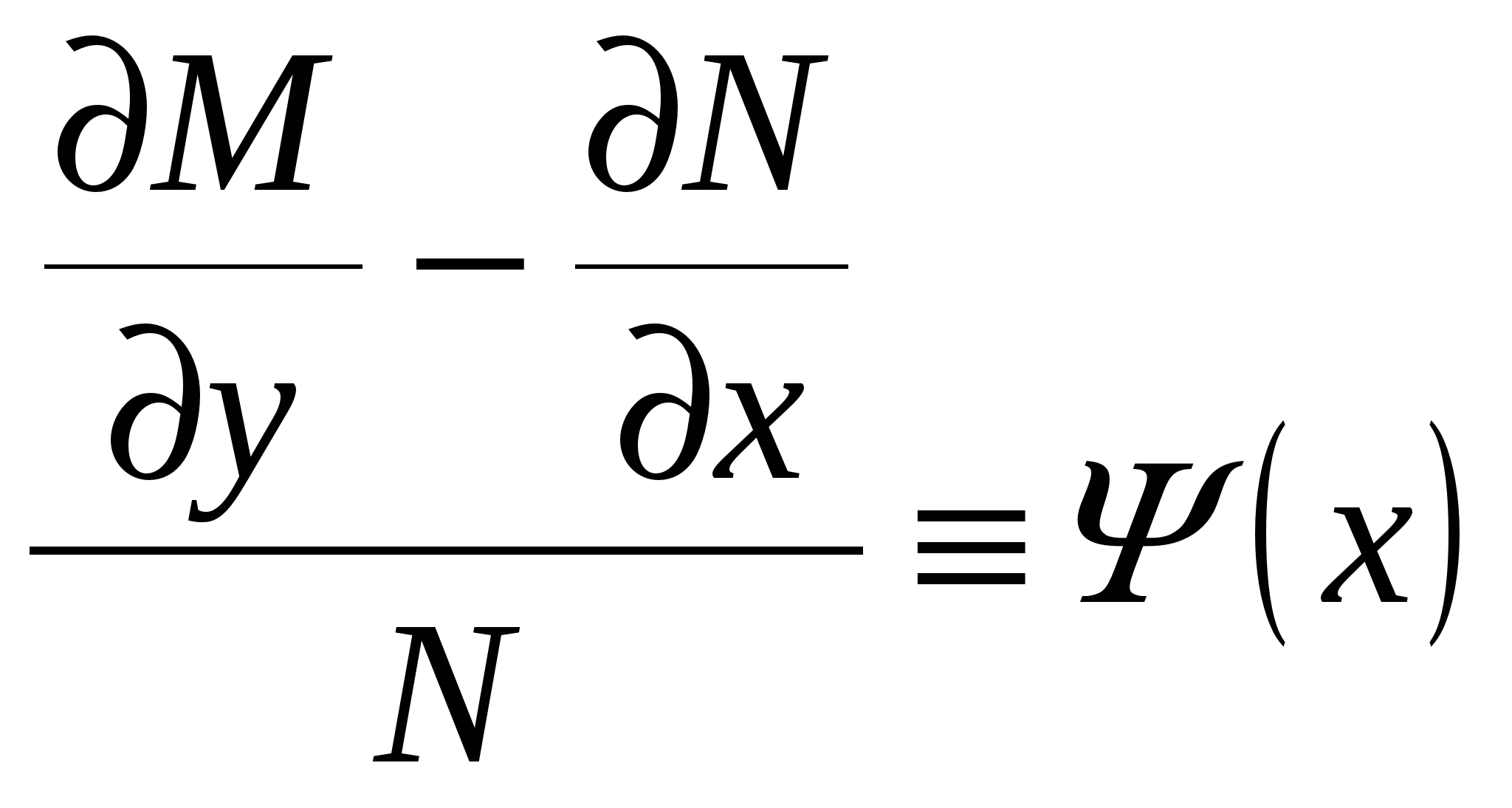 , , или 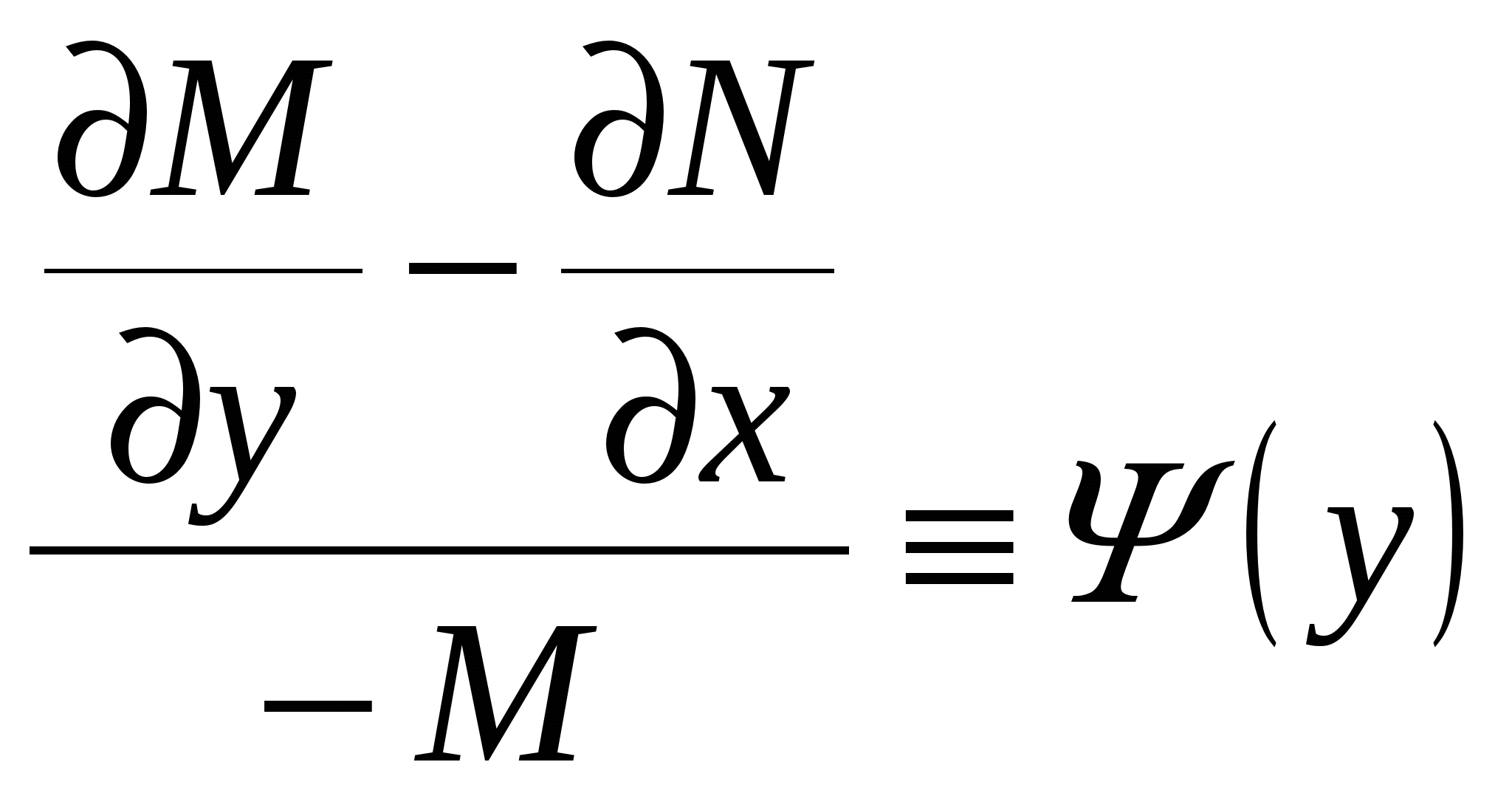 , , |
