пизда физическая. МАТЕМАТИКА РГР 2. Дифференциальные уравнения 1
 Скачать 22.3 Kb. Скачать 22.3 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уральский государственный университет путей сообщения» (ФГБОУ ВПО УрГУПС) Кафедра «Естественнонаучные дисциплины» Контрольная работа №2 по дисциплине «Математика» на тему «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ – 1» Проверил: Выполнил: к.ф.-м.н., доцент студент группы СЖДт-111 Ие Ольга Николаевна Кощеев П.Д. Екатеринбург 2022 г. Вариант №6 01-09. Найти общий интеграл дифференциального уравнения в виде неявно заданной функции F(x, y) = C. Найти частный интеграл дифференциального уравнения, соответствующий указанному начальному условию. Сделать проверку этого ответа с помощью правила дифференцирования неявной функции. 06. y' 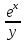 , y(0) 1 , y(0) 1(1) y' 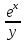 - Это Dy c разделяющимися переменными: - Это Dy c разделяющимися переменными: 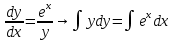 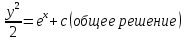 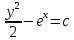 ( общий интеграл) ( общий интеграл)F(x,y)= 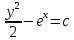 y(0)=1 , отсюда 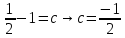 Частный интеграл: 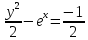 Проверка: У нас F(x,y)= 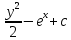 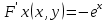 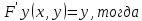 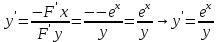  11-19. Найти общее решение дифференциального уравнения в виде явно заданной функции y= y(x) по методу Бернулли. Сделать проверку этого ответа. 11-19. Найти общее решение дифференциального уравнения в виде явно заданной функции y= y(x) по методу Бернулли. Сделать проверку этого ответа.16. 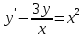 (1) (1)Это линейная 2y первого порядка. Метод Бернулли. Замена: 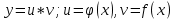 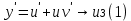 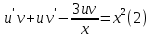 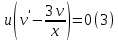 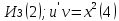 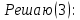 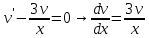 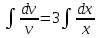 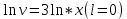 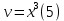  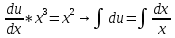 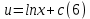 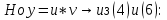 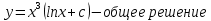 Проверка: 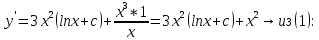 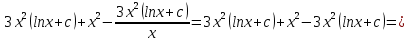 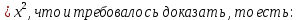 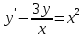 21-29. Найти общее решение дифференциального уравнения второго порядка заменой y p(х). Сделать проверку этого ответа двойным дифференцированием. 26. (1 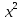 ) y 2xy (1) ) y 2xy (1)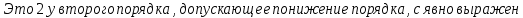 ным аргументом Х (функция у выражена неявно). Замена: 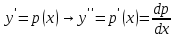 Из (1): (1+ 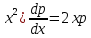 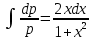 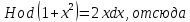 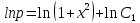 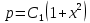 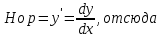 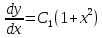 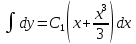 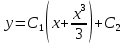 (общее решение) (общее решение)Проверка: 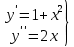 Из (1): Из (1):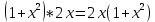 |
