Высшая математика 3. Задание 1. Дифференциальные уравнения первого порядка с разделяющимися переменными. Высшая математика З.1. Дифференциальные уравнения первого порядка с разделяющимися переменными
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Кафедра «Электроснабжение и электротехника» 13.03.02 Электроэнергетика и электротехника. Электроснабжение задание №1 по учебному курсу «Высшая математика»
Тольятти 2023 Вариант 5 Задача 1: Изучить теоретический материал по теме «Дифференциальные уравнения первого порядка с разделяющимися переменными». Найти общее решение дифференциального уравнения первого порядка. Подставить в общее решение дифференциального уравнения первого порядка заданные начальные условия, выразив затем константу. Получить частное решение дифференциального уравнения первого порядка. Решение: а) 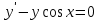 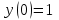 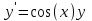 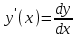 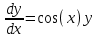 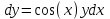 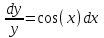 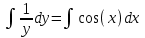 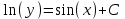 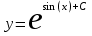 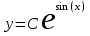 x=0 y=1 1=C C=1 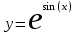 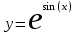 при при 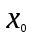 =0, =0, 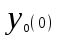 =1 =1б) 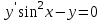 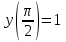 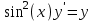 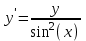 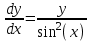 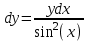 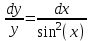 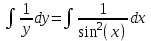 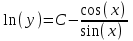 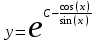 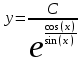 При x= 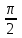 , y=1 , y=11=C, C=1 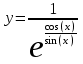 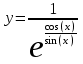 при при 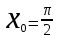 , , 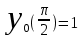 Ответ: а) 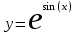 при при 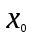 =0, =0, 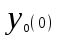 =1 =1б) 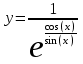 при при 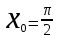 , , 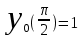 Задача 2: Изучить теоретический материал по теме «Дифференциальные уравнения первого порядка с разделяющимися переменными». Найти многочлен второго порядка. Выделить полный квадрат. После этого перейти к разделению переменных. Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций. Решение: 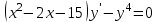 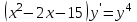 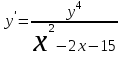 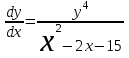 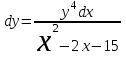 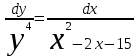 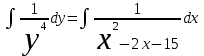 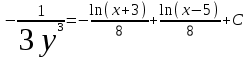 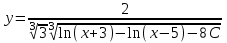 Ответ: 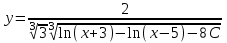 |
