Задание по математике и решение. Задание 1 (3 вариант). Дифференциальные уравнения первого порядка с разделяющимися переменными
 Скачать 47.4 Kb. Скачать 47.4 Kb.
|
|
Рекомендации по выполнению задачи 1 Изучить теоретический материал по теме «Дифференциальные уравнения первого порядка с разделяющимися переменными». Найти общее решение дифференциального уравнения первого порядка. Подставить в общее решение дифференциального уравнения первого порядка заданные начальные условия, выразив затем константу. Получить частное решение дифференциального уравнения первого порядка. Рекомендации по выполнению задачи 2 Изучить теоретический материал по теме «Дифференциальные уравнения первого порядка с разделяющимися переменными». Найти многочлен второго порядка. Выделить полный квадрат. После этого перейти к разделению переменных. Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций. Задача 1. Даны дифференциальные уравнения первого порядка с разделяющимися переменными и их начальные условия. Найти общие решения этих уравнений и определить частные решения.
Задача 2. Решить дифференциальное уравнение первого порядка.
Бланк выполнения заданияЗадача 1 (формулировка полностью): Даны дифференциальные уравнения первого порядка с разделяющимися переменными и их начальные условия. Найти общие решения этих уравнений и определить частные решения. а) 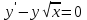 , , 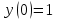 б) 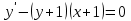 , , 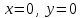 Решение: а) Разделим переменные: 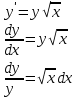 Интегрируем обе части уравнения: 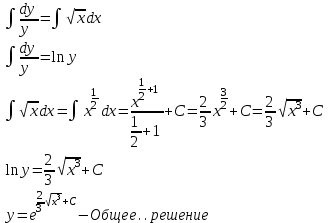 Найдем частное решение: 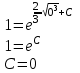 Частное решение имеет вид: 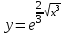 . .б) 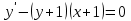 , , 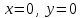 Разделим переменные: 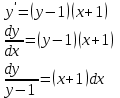 Интегрируем обе части уравнения: 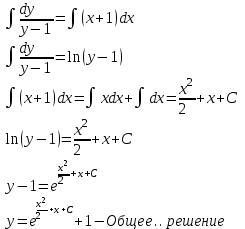 Найдем частное решение: 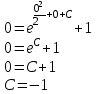 Частное решение имеет вид: 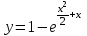 . .Ответ: а) 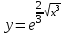 ; б) ; б) 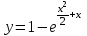 Задача 2 (формулировка полностью): Решить дифференциальное уравнение первого порядка. 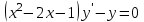 Решение: Разделим переменные: 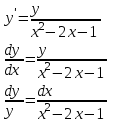 Интегрируем обе части уравнения: 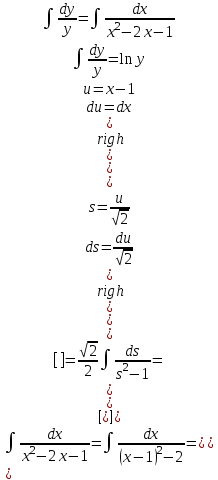 Ответ: 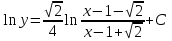 . . |