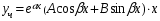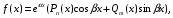Лекции-дифференциальные уравнения. Дифференциальные уравнения
 Скачать 473.05 Kb. Скачать 473.05 Kb.
|
                   Министерство образования и науки российской федерации Министерство образования и науки российской федерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ» Волгодонский инженерно-технический институт - филиал НИЯУ МИФИКонспект лекций по теме: «Дифференциальные уравнения» Волгодонск  Дифференциальные уравнения Дифференциальные уравненияВведение При изучении некоторых явлений часто возникает ситуация, когда процесс не удаётся описать с помощью уравнения y=f(x) или F(x;y)=0. Помимо переменной х и неизвестной функции , в уравнение входит производная этой функции. Определение: Уравнение, связывающее переменную х, неизвестную функцию y(x) и её производные называется дифференциальным уравнением. В общем виде дифференциальное уравнение выглядит так: F(x;y(x);  ; ; ;...;y(n))=0 ;...;y(n))=0Определение: Порядком дифференциального уравнения называется порядок входящей в него старшей производной. 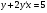 – дифференциальное уравнение 1 порядка – дифференциальное уравнение 1 порядка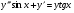 – дифференциальное уравнение 3 порядка – дифференциальное уравнение 3 порядкаОпределение: Решением дифференциального уравнения является функция, которая при подстановке в уравнение обращает его в тождество. Дифференциальные уравнения 1 порядка Определение: Уравнение вида 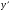 =f(x;y) или F(x;y; =f(x;y) или F(x;y;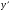 )=0 называется дифференциальным уравнением 1 порядка. )=0 называется дифференциальным уравнением 1 порядка.Определение: Общим решением дифференциального уравнения 1 порядка называется функция y=γ(x;c), где (с –const), которая при подстановке в уравнение обращает его в тождество. Геометрически на плоскости общим решением соответствует семейство интегральных кривых, зависящих от параметра с. y(x0)=y0 Определение: Интегральная кривая, проходящая через точку плоскости с координатами (х0;y0) соответствует частному решению дифференциального уравнения, удовлетворяющего начальному условию: Примеры: 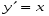 Теорема о существовании единственности решения дифференциального уравнения 1 порядка Дано дифференциальное уравнение 1 порядка 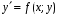 и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0) и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0) D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0 D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0Через точку плоскости с данными координатами проходит 1 интегральная кривая. Если не удаётся получить общее решение дифференциального уравнения 1 порядка в явном виде, т.е 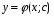 , то его можно получить в неявном виде: , то его можно получить в неявном виде:F(x; y; c) =0 – неявный вид Общее решение в таком виде называется общим интегралом дифференциального уравнения. По отношению к дифференциальному уравнению 1 порядка ставится 2 задачи: 1)Найти общее решение (общий интеграл) 2)Найти частное решение (частный интеграл) удовлетворяющее заданному начальному условию. Эту задачу называют задачей Коши для дифференциального уравнения. Дифференциальные уравнения с разделяющимися переменными Уравнения вида: 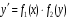 называется дифференциальным уравнением с разделяющимися переменными. называется дифференциальным уравнением с разделяющимися переменными.Подставим 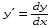 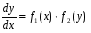 умножим на dx 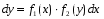 разделим переменные разделим на 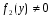 Замечание: обязательно нужно рассматривать частный случай, когда 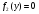 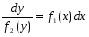 переменные разделены проинтегрируем обе части уравнения 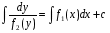 - общее решение - общее решение Дифференциальное уравнение с разделяющимися переменными можно записать в виде: 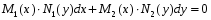 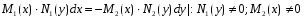 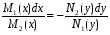 Отдельный случай 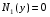 ! !Проинтегрируем обе части уравнения: 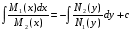 Примеры: 1) 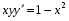 2) 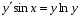 нач. условия: нач. условия: 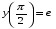 Однородные дифференциальные уравнения 1 порядка Определение: Функция 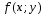 называется однородной порядка n, если называется однородной порядка n, если 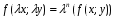 Пример: 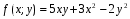 - однородная функция порядка n=2 - однородная функция порядка n=2Т.к 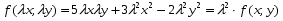 Определение: Однородная функция порядка 0 называется однородной. Определение: Дифференциальное уравнение 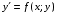 называется однородным, если называется однородным, если 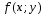 - однородная функция, т.е - однородная функция, т.е 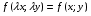 Заменим 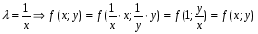 Таким образом однородное дифференциальное уравнение может быть записано в виде: 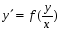 С помощью замены 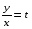 , где t – функция переменной х, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными. , где t – функция переменной х, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными.Замена 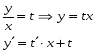 - подставим в уравнение - подставим в уравнение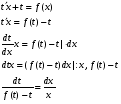 Переменные разделены, проинтегрируем обе части уравнения 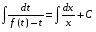 Сделаем обратную замену, подставив вместо 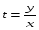 , получим общее решение в неявном виде. , получим общее решение в неявном виде.Пример: 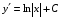 Однородное дифференциальное уравнение может быть записано в дифференциальной форме. M(x;y)dx+N(x;y)dy=0, где M(x;y) и N(x;y) – однородные функции одинакового порядка. Разделим на dx и выразим 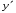 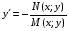 Пример: 1) 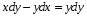 Линейные дифференциальные уравнения 1 порядка Линейные дифференциальные уравнения это вида 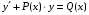 , где P(x), Q(x) – непрерывные функции. , где P(x), Q(x) – непрерывные функции.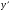 и и 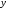 входят в уравнение линейно, т.е не перемножаются между собой. входят в уравнение линейно, т.е не перемножаются между собой.Сделаем замену: 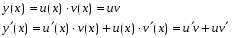 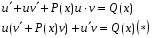 Приравняем скобку к 0 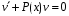 подставим подставим 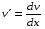 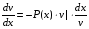 - дифференциальное уравнение с разделяющимися переменными. - дифференциальное уравнение с разделяющимися переменными.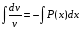 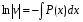 константу интегрирования не прибавляем, т.к достаточно одного частного решения. константу интегрирования не прибавляем, т.к достаточно одного частного решения.Выразим явно 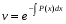 Подставим 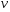 в (*) в (*) 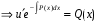 Выразим 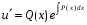 Т.к 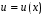 , то проинтегрируем обе части последнего уравнения по х , то проинтегрируем обе части последнего уравнения по х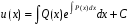 Общее решение линейного уравнения: 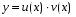 - всегда получается в явном виде. - всегда получается в явном виде.Пример:  1) 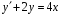  2) 2) 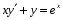 y(1)=2 y(1)=2Уравнения Бернулли 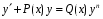 , где , где 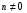 ;1 ;1Решаются такие уравнения так же как и линейные Замена 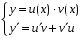 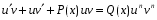 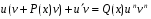 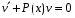 Явно 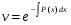   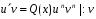 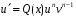 - дифференциальное уравнение с разделяющимися переменными. - дифференциальное уравнение с разделяющимися переменными.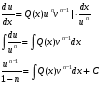 выразим явно u и найдём общее решение 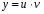 Примеры: 1) 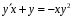 Дифференциальные уравнения высших порядков Определение: Дифференциальное уравнение порядка n называется уравнение вида: 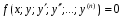 уравнение вида: 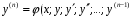  – называется уравнением разрешенным относительно старшей производной. Для такого уравнения справедлива теорема Коши. – называется уравнением разрешенным относительно старшей производной. Для такого уравнения справедлива теорема Коши.Теорема Коши. Если функция 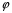 в (*) непрерывна вместе с частными производными: в (*) непрерывна вместе с частными производными: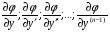 в области содержащей значения в области содержащей значения 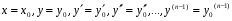 , то существует единственное решение дифференциального уравнения , то существует единственное решение дифференциального уравнения  удовлетворяющее начальным условиям: удовлетворяющее начальным условиям: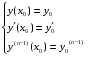 Замечание: для дифференциальных уравнений 2 порядка 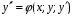 начальные условия имеют вид: 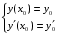 Решить дифференциальное уравнение порядка n означает: 1)Найти общее решение (общий интеграл) 2)Найти частное решение (частный интеграл), удовлетворяющее заданным условиям. Определение: Общим решением дифференциального уравнения 2 порядка 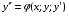 является функция является функция 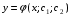 , такая что: , такая что:1) при любых значениях с1 и с2 эта функция – решение. 2) каковы бы ни были начальные условия на области, в которой выполняется теорема Коши всегда можно подобрать значения с1 и с2 удовлетворяющие начальным условиям. Определение: Частным решением дифференциального уравнения 2 порядка является решение, при конкретных значениях с1 и с2. Замечание: общее решение дифференциального уравнения 2 порядка может быть получено в неявном виде: 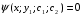 Дифференциальные уравнения 2 порядка, допускающие понижение порядка 1) Уравнения вида: 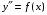 уравнение решается двукратным интегрированием по переменной х. Проинтегрируем 1 раз по х. 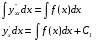 Проинтегрируем 2 раз по х 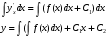 общее решение. Замечание: для дифференциального уравнения порядка n: 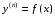 - интегрировать нужно n раз. - интегрировать нужно n раз.Примеры: 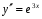 2) Дифференциальные уравнения не содержащие явно y. 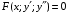 - нет явно y - нет явно yЗамена 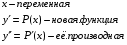 Подставим замену в дифференциальное уравнение, получим 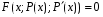 получим дифференциальное уравнение 1 порядка. Найдём решение этого уравнения: 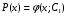 сделаем обратную замену 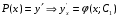 проинтегрируем обе части по х 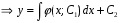 - общее решение - общее решениеПример: 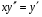 3) Дифференциальные уравнения 2 порядка не содержащие явно х. 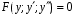 - нет явно х. - нет явно х.Замена: у-новая переменная 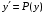 - новая функция - новая функция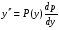 - её производная - её производнаяПодставим замену в исходное уравнение 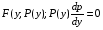 получим дифференциальное уравнение 1 порядка: 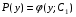 - его решение - его решениеСделаем обратную замену - 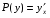 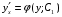 - дифференциальное уравнение с разделяющимися переменными. Разделим переменные: - дифференциальное уравнение с разделяющимися переменными. Разделим переменные: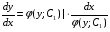 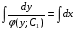 ; ; 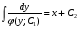 - общее решение (вид неявный) - общее решение (вид неявный)Примеры: 1. 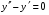 2. 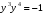 Линейные дифференциальные уравнения высших порядков Уравнение вида: 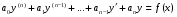 называется линейным дифференциальным уравнением высшего порядка, где a0,а1,…аn-функции переменной х или константы, причём a0,а1,…аn и f(x) считаются непрерывными. называется линейным дифференциальным уравнением высшего порядка, где a0,а1,…аn-функции переменной х или константы, причём a0,а1,…аn и f(x) считаются непрерывными.Если a0=1(если 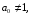 то на него можно разделить) то на него можно разделить)  уравнение примет вид: уравнение примет вид: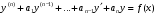 Если 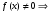 уравнение неоднородное. уравнение неоднородное.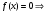 уравнение однородное. уравнение однородное.Линейные однородные дифференциальные уравнения порядка n Уравнение вида: 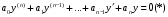 называются линейными однородными дифференциальными уравнениями порядка n. называются линейными однородными дифференциальными уравнениями порядка n.Для этих уравнений справедливы следующие теоремы: Теорема 1: Если 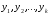 - решение - решение , то сумма , то сумма 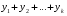 - тоже решение - тоже решение  Доказательство: подставим сумму в  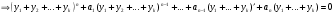 Т.к производная любого порядка от суммы равна суме производных, то можно перегруппироватся , раскрыв скобки: 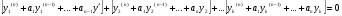 т.к y1 и y2 – решение. 0=0(верно)  сумма тоже решение. сумма тоже решение.теорема доказана. Теорема 2: Если y0-решение  , то , то 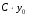 - тоже решение - тоже решение  . .Доказательство: Подставим 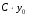 в уравнение в уравнение 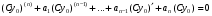 т.к С выносится за знак производной, то 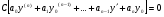  т.к 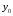 решение, 0=0(верно) решение, 0=0(верно) Сy0-тоже решение. Сy0-тоже решение.теорема доказана. Следствие из Т1 и Т2: если 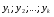 - решения (*) - решения (*)  линейеая комбинация линейеая комбинация 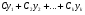 -тоже решение (*). -тоже решение (*).Линейно независимые и линейно зависимые системы функций. Определитель Вронского и его свойства Определение: Система функций 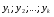 - называется линейно независимой , если линейная комбинация - называется линейно независимой , если линейная комбинация 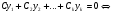 коэффициенты коэффициенты 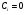 . .Определение: Систему функций 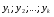 - называют линейно зависимой, если - называют линейно зависимой, если 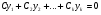 и есть коэффициенты и есть коэффициенты 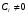 . .Возьмём систему двух линейно зависимых функций 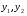 т.к т.к 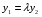 или или 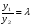 - условие линейной независимости двух функций. - условие линейной независимости двух функций.Примеры: 1) 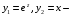 линейно независимы линейно независимы 2) 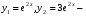 линейно зависимы линейно зависимы3) 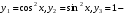 линейно зависимы линейно зависимыОпределение: Дана система функций 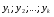 - функций переменной х. - функций переменной х.Определитель 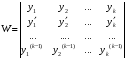 - определитель Вронского для системы функций - определитель Вронского для системы функций 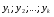 . .Для системы двух функций определитель Вронского выглядит следующим образом: 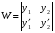 Свойства определителя Вронского:
Теорема: Об общем решении линейного однородного дифференциального уравнения 2 порядка. Если y1 и y2 – линейно независимые решения линейного однородного дифференциального уравнения 2 порядка, то 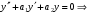 общее решение имеет вид: общее решение имеет вид: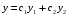 Доказательство: 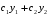 - решение по следствию из Т1 и Т2. - решение по следствию из Т1 и Т2.Если даны начальные условия то 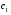 и и 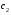 должны находится однозначно. должны находится однозначно.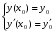 - начальные условия. - начальные условия.Составим систему для нахождения 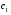 и и 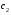 . Для этого подставим начальные условия в общее решение. . Для этого подставим начальные условия в общее решение.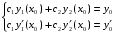 определитель этой системы: 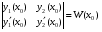 - определитель Вронского, вычисленный в точке х0 - определитель Вронского, вычисленный в точке х0т.к 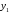 и и 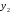 линейно независимы линейно независимы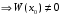 (по 20) (по 20)т.к определитель системы не равен 0, то система имеет единственное решение и 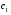 и и 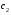 находятся из системы однозначно. находятся из системы однозначно. 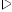 Общее решение линейного однородного дифференциального уравнения порядка n 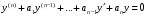 (*) (*)Можно показать что уравнение имеет n линейно независимых решений 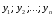 Определение: n линейно независимых решений 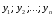 линейного однородного дифференциального уравнения порядка n называется фундаментальной системой решения. линейного однородного дифференциального уравнения порядка n называется фундаментальной системой решения. Общее решение линейного однородного дифференциального уравнения порядка n , т.е (*) – линейная комбинация фундаментальной системы решений: Общее решение линейного однородного дифференциального уравнения порядка n , т.е (*) – линейная комбинация фундаментальной системы решений: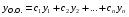 , где , где 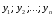 - фундаментальная система решения. - фундаментальная система решения.Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами Это уравнения вида: 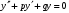 , где p и g – числа(*) , где p и g – числа(*)Определение: Уравнение 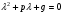 - называется характеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи: - называется характеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи:1)D>0 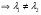 - два действительных различных решения. - два действительных различных решения.2)D=0 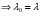 - один действительный корень кратности 2. - один действительный корень кратности 2.3)D<0 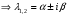 - два комплексно сопряжённых корня. - два комплексно сопряжённых корня.Для каждого из этих случаев укажем фундаментальную систему решений, составленную из 2 функций 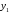 и и 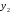 . .Будем показывать что: 1) 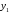 и и 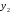 - ЛНЗ - ЛНЗ2) 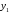 и и 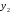 - решение (*) - решение (*)Рассмотрим 1 случай D>0 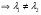 - 2 действительных различных корня. - 2 действительных различных корня.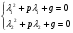 Характеристическое уравнение: Характеристическое уравнение: 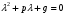 В качестве ФСР возьмём: 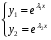 а) покажем ЛНЗ 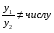 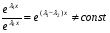 б) покажем, что  - решение (*), подставим - решение (*), подставим 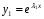 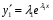 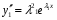 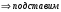 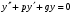 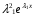 + p + p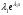 +g +g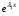 =0 =0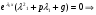 верное равенство верное равенство  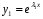 решение (*) решение (*)аналогично показывается для y2. Вывод: 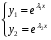 - ФСР (*) - ФСР (*)  общее решение общее решение 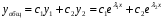 Рассмотрим 2случай: D=0 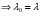 - 1 действительный корень кратности 2. - 1 действительный корень кратности 2.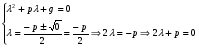 В качестве ФСР возьмём: 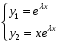 ЛНЗ: 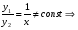 ЛНЗ есть. ЛНЗ есть.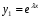 - решение уравнения (см. 1 случай). Покажем что - решение уравнения (см. 1 случай). Покажем что 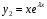 - решение. - решение.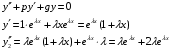 подставим в ДУ 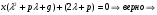 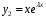 - решение. - решение.Вывод: ФСР 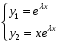 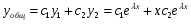 Пример: 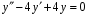 3 случай: D<0 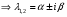 - 2 комплексно сопряжённых корня. - 2 комплексно сопряжённых корня.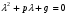 подставим 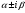 в характ. уравнение в характ. уравнение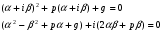 комплексное число равно 0, когда действительная и мнимая часть равны 0. 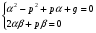 - будем использовать. - будем использовать.Покажем, что 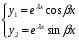 - образуют ФСР. - образуют ФСР.А)ЛНЗ: 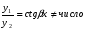 Б) 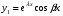 - решение ДУ - решение ДУ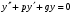 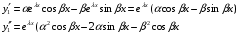 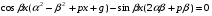 верное равенство 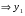 - решение ДУ. - решение ДУ.Аналогично показывается, что 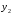 тоже решение. тоже решение.Вывод: ФСР: 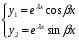 Общее решение: 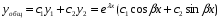 Пример: 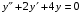 Если заданы н.у. 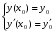 - то сначала находят общее решение - то сначала находят общее решение 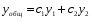 , его производную: , его производную: 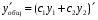 , а потом в эту систему подставляют н.у и находят , а потом в эту систему подставляют н.у и находят 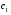 и и 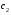 . .Пример: 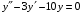 Н.у: Н.у: 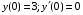 Линейные однородные ДУ порядка n с постоянными коэффициентами Это уравнения вида: 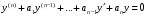 , где аi – числа. , где аi – числа.Характеристическое уравнение будет иметь вид: 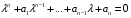 Слева стоит многочлен степени n, который имеет n корней с учётом их кратности и комплексности, следовательно, ФСР будет состоять из n решений:
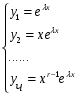
Общее решение уравнения – линейная комбинация фундаментальных решений 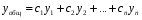 Основная трудность состоит в том, чтобы правильно решить характеристическое уравнение. Пример: 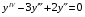 Линейные неоднородные ДУ Это уравнения вида: 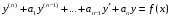  Теорема об общем решении ДУ: Общее решение ДУ(*) имеет вид: 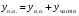 , где , где 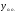 - общее решение соответствующего однородного уравнения. - общее решение соответствующего однородного уравнения.Доказательство: подставим  в в  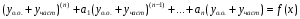 раскроем скобки и перегруппируемся: 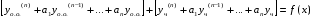 (верно) (верно)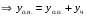 Если даны н.у 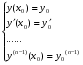 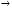 нужно показать, что все константы находятся однозначно нужно показать, что все константы находятся однозначно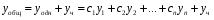 , где ФСР , где ФСР 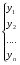 Продифференцируем 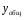 нужное количество раз и подставим н.у нужное количество раз и подставим н.у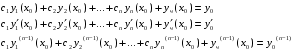 получим систему n-линейных уравнений с n неизвестными 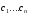 . Определитель этой системы . Определитель этой системы 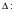 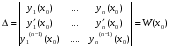 - определитель Вронского системы функций - определитель Вронского системы функций 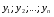 . .Т.к 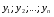 - ФСР - ФСР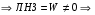 линейная система имеет единственное решение и все константы находятся однозначно. линейная система имеет единственное решение и все константы находятся однозначно.Конец доказательства. Замечание: Общее решение соответствующего однородного уравнения 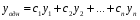 - линейная комбинация ФСР – известно - линейная комбинация ФСР – известноОсновная трудность нахождения yч – решения неоднородного уравнения. Линейные неоднородные ДУ 2 порядка с постоянными коэффициентами со специальной правой частью. Рассм. ДУ 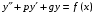 Общее решение такого уравнения: 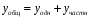 , где , где 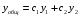 ФСР 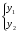 - уже рассматривали - уже рассматривалиУкажем метод нахождения частного решения неоднородного уравнения 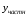 , если f(x) имеет специальный вид. , если f(x) имеет специальный вид.Рассмотрим следующие случаи: I. 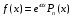 , где , где 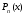 - многочлен степени n. - многочлен степени n.а) 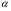 - не корень характеристического уравнения - не корень характеристического уравнения  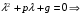 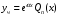 , где , где 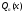 - многочлен степени n с неопределенными буквенными коэффициентами. Подставим - многочлен степени n с неопределенными буквенными коэффициентами. Подставим 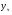 в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы. в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.б) 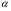 - корень характеристического уравнения кратности 1 - корень характеристического уравнения кратности 1  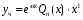 в) 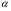 - корень характеристического уравнения кратности 2 - корень характеристического уравнения кратности 2  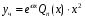
a) 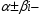 не корень характеристического уравнения не корень характеристического уравнения 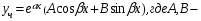 неопределенные коэффициенты.Подставив неопределенные коэффициенты.Подставив 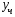 в ДУ и приравняв коэффициенты при в ДУ и приравняв коэффициенты при 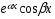 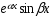 находим А и В находим А и Вб) 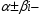 корень характеристического уравнения кратности 1 корень характеристического уравнения кратности 1
Замечание : Если в правой части  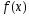 есть только есть только 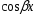 или или 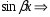 в частном решении 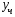 должны быть и sin и cos , т.е тригонометрия должна быть полной. должны быть и sin и cos , т.е тригонометрия должна быть полной.
Где 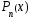 , ,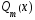 -многочлены степеней m и n -многочлены степеней m и na) 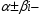 не корень характеристического уравнения не корень характеристического уравнения  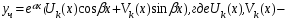 многочлены степени к с неопределенными коэффициентами многочлены степени к с неопределенными коэффициентамиб) 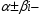 корень характеристического уравнения корень характеристического уравнения 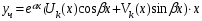 Метод вариации Рассмотрим ДУ: 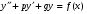 Где правая часть f(x) произвольного вида (необязательно специального). Общее решение соответствующего однородного уравнения: 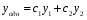 , где , где  и и  - произвольные const, - произвольные const, 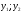 - ФСР. - ФСР.Будем варьировать 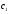 и и 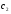 и считать, что и считать, что 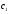 и и 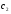 зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде: зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде: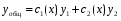 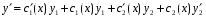 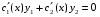 (*) (*)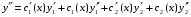 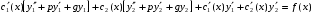 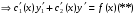 объединим  и и 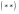 в систему в систему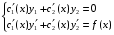 - эта система для нахождения - эта система для нахождения 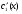 и и 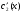 имеет единственное решение, т.к определитель системы имеет единственное решение, т.к определитель системы 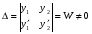 , ,для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера 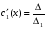 , где , где 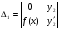 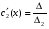 , где , где 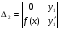 решая систему получим 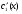 и и 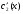 , проинтегрируем полученные функции по переменной х. , проинтегрируем полученные функции по переменной х.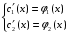 - проинтегрируем по х - проинтегрируем по х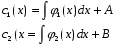 , где А и В – константы интегрирования , где А и В – константы интегрированияТаким образом общее решение неоднородного уравнения: 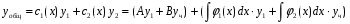 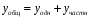 Пример: 1) 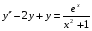 Решение систем линейных ДУ 1 порядка с постоянными коэффициентами способом подстановки Рассмотрим систему ДУ 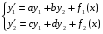 , где a,b,c,d – числа. , где a,b,c,d – числа.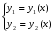 - искомая функция - искомая функция 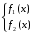 - функции переменной х - функции переменной хпродифференцируем по переменной х первое уравнение системы: Дифф.(1) 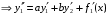 Подставим из (2) 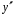 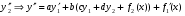 подставим из (1) 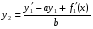 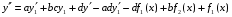 перенесем слагаемые с 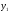 и и 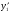 налево налево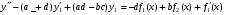 получим линейное неоднородное ДУ 2 порядка с постоянными коэффициентами. Решая это уравнение получим 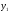 , продифференцируем , продифференцируем 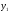 и найдём и найдём 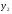 . .Пример: 1) 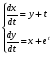 начальные условия: начальные условия: 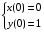 . . |

 на этом отрезке.
на этом отрезке.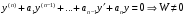 при любых значениях х в области, где определены функции а1…аn
при любых значениях х в области, где определены функции а1…аn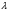 , (имеющему кратность 1) ставится в соответствие
, (имеющему кратность 1) ставится в соответствие 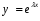
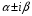
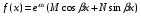 ,где M,Nчисла
,где M,Nчисла