Дифференциалы_grad_произв по направл. Дифференциалы Условия полного дифференциала 2 перем (свво плоского потенциального поля) 3 перем
 Скачать 1.48 Mb. Скачать 1.48 Mb.
|
|
Дифференциалы 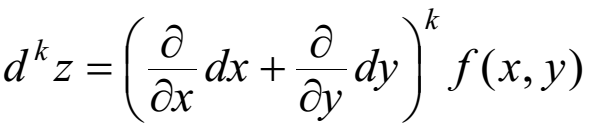 Условия полного дифференциала 2 перем 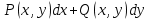 3 перем ![$\[\left\{ \begin{array}{l} \frac{{\partial u}}{{\partial x}} = p(x,y,z)\\ \frac{{\partial u}}{{\partial y}} = q(x,y,z)\\ \frac{{\partial u}}{{\partial z}} = r(x,y,z) \end{array} \right.\]$](48958_html_22845e5d.png) Если это верно (т.е. такая функция U существ), то Если расписать покомпонентно 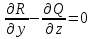 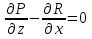 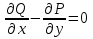 МВТУ зад.3 Найти дифф-л 2 порядка функции 3 перем 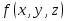 в точке в точке 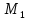 и дифф-л 3 порядка функции и дифф-л 3 порядка функции 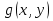 в точке в точке 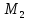  Зад 5. Проверить явл ли данная дифференц форма дифф-лом некот ф-ии и найти ее 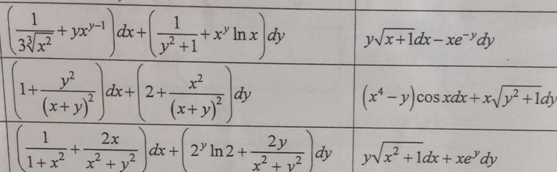 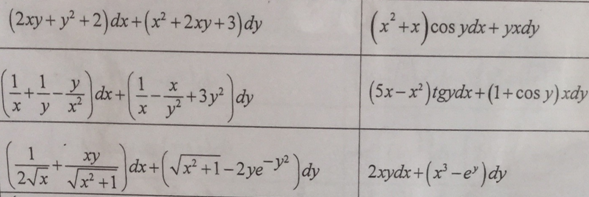 Градиент, производная по направлению. Уравнения касательной плоскости и нормали Если в то Геом смысл произв по направл пл-ть, прох через луч «эль» перпенд пл-и Прим: также мсказать, что Градиентом функции \ уравнение касательной плоскости к данной поверхности в т канонические уравнения нормали по точке МВТУ зад.6 В т.А найти производную функции 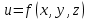 по направлению вектора AB и мах производную по направлению. Указать вектор направления максимальной производной по направлению вектора AB и мах производную по направлению. Указать вектор направления максимальной производной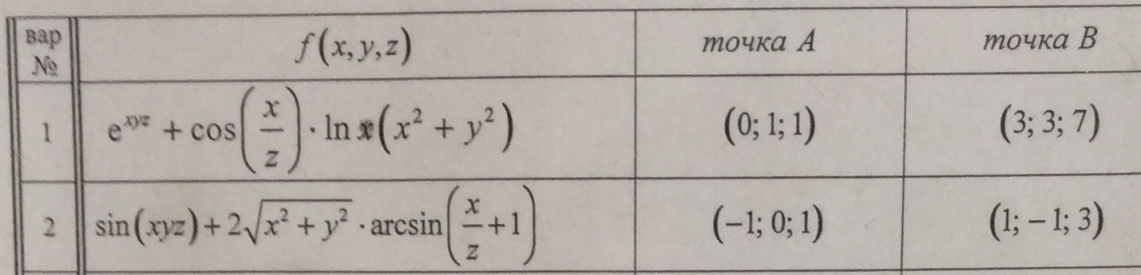  МВТУ Зад 7 На поверхности заданной уравнением 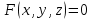 найти точки в кот касательная плоскость перпендикулярна заданному вектору найти точки в кот касательная плоскость перпендикулярна заданному вектору 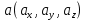 . Длякаждой их найденнточек записать уравнение касательной и нормали . Длякаждой их найденнточек записать уравнение касательной и нормали Акад при президенте РАНХ и ГСМатем анализ I курс, II сем, II поток, контр раб № 11.Для функции u=ln(2+xy+y)-3 построить: а) линию уровня, проходящую через точку M(-2, 1); (1) б) градиент функции u в точке M; (1) в) карту линий уровня (достаточно 3-х линий); (1) г) на какой линии достиг наиб зн функции? Ответ обосн. (1) д) написать уравнение касательной к графику функции в т. М (1)
3. Найти экстремум функции 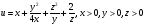 . (4) . (4)4. Найти экстремум ф u=5x-3y при усл 11x2+9xy+y2+4=0 (исп ф Лагранжа). (5) 5.Иссл ф z= 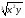 на дифференцир в т М(0,0) (4) (рассм функц z= на дифференцир в т М(0,0) (4) (рассм функц z=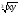 , z= , z= , z= , z=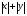 ) ) 6. Задана квадратичная форма 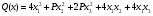 в в 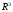 . . а)Найдите все значения параметра Р, при кот квадратичная форма положит определена б)При Р=1 приведите квадр форму к канонич виду методом Лагранжа послед выдел полных квадратов и выпиш выр новых координат через старые.(3) |
