фыфы. Динамическое программирование
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
Ещё пример задания:Р-03. Исполнитель Май4 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера: 1. прибавь 1 2. прибавь 2 3. прибавь 4 Первая из них увеличивает число на экране на 1, вторая увеличивает это число на 2, а третья – на 4. Программа для исполнителя Май4 – это последовательность команд. Сколько есть программ, которые число 21 преобразуют в число 30? Решение (1 способ, составление таблицы): заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) все числа, меньшие начального числа 21, с помощью этого исполнителя получить нельзя, для них количество программ будет равно 0 для начального числа 21 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды; если через теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую любое число N > 21 могло быть получено одной из трёх операций сложения соответственно из чисел N-1, N-2 и N-4, поэтому остается по этой формуле заполнить таблицу для всех значений от 21 до 30:
ответ – 96. Решение (программа на Python, Б.С. Михлин): полная программа: t = 30 # цель (target) # Функция подсчета количества цепочек команд (программ). # x - текущее число. def nProg( x ): if x == t: # если цель достигнута, то return 1 # завершить функцию, посчитав цепочку (программу) if x > t: # если перелет, то return 0 # завершить функцию, не считая цепочку # x < t - продолжаем строить дерево: return nProg( x + 1 ) + nProg( x + 2 ) + nProg( x + 4 ) print( nProg( 21 ) ) Ответ: 96. Ещё пример задания:Р-02. У исполнителя Утроитель две команды, которым присвоены номера: 1. прибавь 1 2. умножь на 3 Первая из них увеличивает число на экране на 1, вторая – утраивает его. Программа для Утроителя – это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 20? Решение (1 способ, составление таблицы): заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) начнем с простых случаев, с которых будем начинать вычисления: для чисел 1 и 2, меньших, чем 3, существует только одна программа, состоящая только из команд сложения; если через теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую если число N не делится на 3, то оно могло быть получено только последней операцией сложения, поэтому если N делится на 3, то последней командой может быть как сложение, так и умножение поэтому для получения если N не делится на 3: если N делится на 3: остается заполнить таблицу для всех значений от 1 до N:
Заметим, что количество вариантов меняется только в тех столбцах, где N делится на 3, поэтому из всей таблицы можно оставить только эти столбцы:
заданное число 20 попадает в последний интервал (от 18 до 21), поэтому … ответ – 12. Решение (2 способ, подстановка – вычисления по формулам «с конца»): п. 1-6 выполняются так же, как и при первом способе; главная задача – получить рекуррентную формулу: если N не делится на 3: если N делится на 3: с начальными условиями начинаем с заданного конечного числа 20; применяем первую формулу ( далее применяем вторую формулу ( применяем первую формулу для 17: применяем вторую формулу для обоих слагаемых: где учтено, что с помощью первой формулы переходим в правой части к числам, делящимся на 3: а затем применяем вторую формулу для каждого слагаемого снова используем первую формулу а затем – вторую: и еще раз ответ – 12. Решение (3 способ, О.В. Шецова, лицей № 6, г. Дубна): будем составлять таблицу из трех столбцов: в первом записывается получаемое число от 1 до 20, во втором – какой последней командой может быть получено это число, а в третьем вычисляем количество различных программ для получения этого числа из 1 очевидно, что число 1 может быть получено с помощью одной единственной (пустой) программы:
число 2 не делится на 3, поэтому его можно получить только командой сложения (+1), значит, количество программ для 2 совпадает с количеством программ для 1:
число 3 делится на 3, поэтому его можно получить с помощью двух команд: +1 (из 2) и *3 (из 1):
числа 4 и 5 не делятся на 3, поэтому их можно получить только с помощью команды +1, а число 6 может быть получено двумя командами:
следующая группа – 7, 8 (не делятся на 3) и 9 (делится на 3):
далее – 10, 11 и 12:
и так далее, вот полностью заполненная таблица (до конечного числа 20):
ответ – количество программ, с помощью которых можно получить число 20 из 1, – считываем из последней ячейки третьего столбца ответ – 12. Решение (4 способ, М.В. Кузнецова и её ученики, г. Новокузнецк): пусть тогда для построения рекуррентной формулы определения какой может быть последняя команда и сколько есть видов этого последнего действия? для каждого «последнего» действия нужно знать число программ получения предыдущего числа, сумма этих количеств и есть искомое значение Например, общее количество программ получения числа 6 с помощью Утроителя равно число программ получения числа составим рекуррентную формулу для определения числа программ получения числа при если если с помощью это формулы заполняем таблицу следующим образом: – в первом столбце записываем все натуральные числа от 1 до заданного – во втором столбце – числа, на единицу меньшие (из которых может быть получено – в третьем столбце для чисел, кратных 3-м, записываем частное от деления числа, записанного в первом столбце, на 3 (из этого числа может быть получено – в последнем столбце вычисляем
ответ – 12. Решение (5 способ, А. Сидоров): основная идея – число программ, преобразующих начальное число 1 в конечное 20 с помощью заданных в условии команд, равно числу программ, преобразующих конечное число 20 в начальное 1 с помощью обратных команд: «вычти 1» и «раздели на 3» будем строить «обратное дерево» – дерево всех способов преобразования конечного числа в начальное; это лучше (в сравнении с построением «прямого» дерева, от начального числа к конечному), потому что операция умножения необратима – каждое число можно умножить на 3, но не каждое можно разделить на 3; из-за этого сразу отбрасываются тупиковые ветви, не дающие новых решений рисуем сокращенное дерево, в котором черные стрелки показывают действие первой команды («прибавь 1»), а красные – действие второй команды («умножь на 3»); красные стрелки подходят только к тем числам, которые делятся на 3: 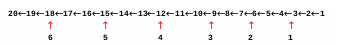 чтобы получить количество программ для каждого числа из верхней строки, нужно сложить соответствующие количества программ для всех чисел из нижнего ряда, которые не больше данного (программы с умножением), и добавить 1 (программа, состоящая из одних сложений) очевидно, что для получения 1 существует одна (пустая) программа; тогда для числа 2 тоже получается одна программа, а для числа 3 – две программы:  далее, для чисел 4 и 5 получаем 2 программы (после числа 3 нет «разветвлений» – подходящих красных стрелок) , а для числа 6 – 3 программы, так как «подошло» еще одно разветвление (6 можно получить умножением 2 на 3), а для числа 2 мы уже подсчитали количество программ – оно равно 1: 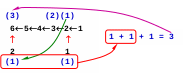 находить число программ для следующих чисел нам уже не понадобится, потому что при умножении на 3 они дают числа, большие, чем заданное конечное число 20 запишем полученные результаты в самой нижней строке для всех множителей от 1 до 6:  теперь остается сложить все числа в скобках в нижнем ряду (количество программ с командами умножения) и добавить 1 (одна программа, состоящая только из команд сложения): 3 + 2 + 2 + 2 + 1 + 1 + 1 = 12 ответ – 12.
Решение (программа на Python, Б.С. Михлин): полная программа: t = 20 # цель (target) # Функция подсчета количества цепочек команд (программ). # x - текущее число. def nProg( x ): if x == t: # если цель достигнута, то return 1 # завершить функцию, посчитав цепочку (программу) if x > t: # если перелет, то return 0 # завершить функцию, не считая цепочку # x < t - продолжаем строить дерево: return nProg( x + 1 ) + nProg( x * 3 ) print( nProg( 1 ) ) Ответ: 12. Еще пример задания:Р-01. У исполнителя Калькулятор две команды, которым присвоены номера: 1. прибавь 1 2. увеличь вторую с конца цифру на 1 Первая из них увеличивает число на экране на 1, вторая – увеличивает на 1 число десятков. Если перед выполнением команды 2 вторая с конца цифра равна 9, она не изменяется. Программа для Калькулятора – это последовательность команд. Сколько есть программ, которые число 15 преобразуют в число 28? Решение (1 способ, составление таблицы): заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) при заданных командах очередное число N может быть получено двумя способами: увеличением на 1 (для всех чисел, больших начального числа) увеличением числа десятков на 1 (то есть, фактически командой «+10») – для всех чисел, больших или равных 25; например, число 24 не может быть получено этой командой (14 + 10 = 24), потому что число 14 меньше, чем начальное значение 15 таким образом, рекуррентные формулы принимают вид других способов получения числа с помощью исполнителя с заданными командами нет, то есть мы таким образом рассматриваем все возможные программы начальное значение: далее заполняем таблицу:
Ответ: 5 Решение (программа на Python, Б.С. Михлин): полная программа: t = 28 # цель (target) # Функция подсчета количества цепочек команд (программ). # x - текущее число. def nProg( x ): if x == t: # если цель достигнута, то return 1 # завершить функцию, посчитав цепочку (программу) if x > t: # если перелет, то return 0 # завершить функцию, не считая цепочку # x < t - продолжаем строить дерево: x1 = x if x1 % 100 // 10 < 9: # число десятков < 9? x1 += 10 return nProg( x + 1 ) + nProg( x1 ) print( nProg( 15 ) ) Ответ: 5. Еще пример задания:Р-00. У исполнителя Калькулятор две команды, которым присвоены номера: 1. прибавь 1 2. увеличь две младшие цифры на 1 Первая из них увеличивает число на экране на 1, вторая – увеличивает на 1 число десятков и число единиц. Если перед выполнением команды 2 какая-либо из двух младших цифр равна 9, она не изменяется. Программа для Калькулятора – это последовательность команд. Сколько есть программ, которые число 23 преобразуют в число 48? Решение (1 способ, составление таблицы): заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) при заданных командах очередное число N может быть получено двумя способами: увеличением на 1 (для всех чисел, больших начального числа) увеличением обеих цифр на 1 в результате выполнения команды 2 (то есть, фактически командой «+11») – для всех чисел, больших или равных 23 + 11 = 34, которые НЕ оканчиваются на 0; увеличением только младшей цифры на 1 в результате выполнения команды 2 (то есть, фактически командой «+1») – для всех чисел от 91 до 99, но в нашем диапазоне (23..48) таких нет увеличением только старшей цифры на 1 в результате выполнения команды 2 (то есть, фактически командой «+10») – для всех чисел, больших 34 и имеющих 9 на конце; в нашем случае под этот вариант подходит только число 39 таким образом, рекуррентные формулы принимают вид других способов получения числа с помощью исполнителя с заданными командами нет, то есть мы таким образом рассматриваем все возможные программы начальное значение: далее заполняем таблицу:
здесь многоточия означают, что для всех чисел от 23 до 33 включительно количество программ равно 1; например, для числа 47 количество программ вычисляется как а для числа 39 –как Ответ: 26 Решение (программа на Python, Б.С. Михлин): полная программа: t = 48 # цель (target) # Функция подсчета количества цепочек команд (программ). # x - текущее число. def nProg( x ): if x == t: # если цель достигнута, то return 1 # завершить функцию, посчитав цепочку (программу) if x > t: # если перелет, то return 0 # завершить функцию, не считая цепочку # x < t - продолжаем строить дерево: x1 = x if x1 % 100 // 10 < 9: # число десятков < 9? x1 += 10 if x1 % 10 < 9: # число единиц < 9? x1 += 1 return nProg( x + 1 ) + nProg( x1 ) print( nProg( 23 ) ) Ответ: 26. |




 1
1


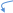
 1 *3
1 *3
 1
1
 1
1
 1 *3
1 *3