Динамика Ньютон. Динамика материальной точки. Законы Ньютона. 1 закон Ньютона
 Скачать 233 Kb.
|
|
Динамика материальной точки. Законы Ньютона. 1 закон Ньютона Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения. Такие системы отсчета называются инерциальными. 2 закон Ньютона Скорость изменения импульса тела  равна результирующей силе  , действующей на тело.  , импульсом Ньютон назвал произведение массы тела на его скорость  . По определению ускорения  , тогда для постоянной массы тела  , тогда  (1)Данное выражение справедливо для протяженных тел, движущихся поступательно относительно инерциальных систем отсчета. При движении тела в неинерциальной системе отсчета, возникает сила инерции, равная произведению массы тела на ускорение системы отсчета. Е  сли тело массой m движется с ускорением a′ относительно неинерциальной системы отсчета, ускорение которой равно А, то ускорение тела относительно инерциальной системы отсчета а, согласно теореме сложения ускорений   . Подставляя это выражение в уравнение (1), получим: , здесь  , поэтому второй закон Ньютона для неинерциальной системы отсчета  (2)3 закон Ньютона Силы взаимодействия двух тел равны по модулю и противоположно направлены. 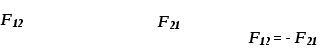 На горизонтально движущееся тело, находящееся на опоре, действуют силы, показанные на рисунке 1. Сила трения зависит только от степени неровности поверхностей и определяется коэффициентом трения μ. Максимальное значение силы трения называется силой трения покоя и равно N∙μ.  Если к грузу прикреплена пружина, на него действует сила упругости пружины, равная F=-kx, где x – деформация пружины, а знак «-» означает, что сила направлена в сторону, противоположную деформации. Коэффициент упругости k показывает какую силу нужно приложить к пружине для ее удлинения или сжатия на 1 м. При последовательном соединении пружин коэффициент упругости может быть найден из соотношения  , при параллельном соединении пружин  Законы Ньютона применимы как для случая прямолинейного, так и криволинейного движения материальной точки. Динамика вращательного движения твердого тела. Для того, чтобы заставить твердое тело двигаться поступательно, достаточно приложить к нему силу или несколько сил. Для того, чтобы привести тело во вращение, необходимо, чтобы минимум две точки твердого тела оставались в состоянии покоя. Прямая, проходящая через такие две точки, называется осью вращения. Если к твердому телу приложены силы, линии действия которых не пересекают ось вращения, говорят, что сила сообщает телу вращающий момент. М 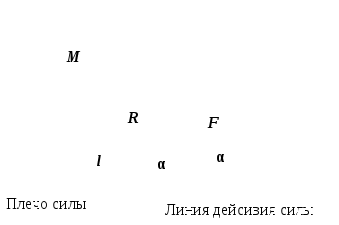 омент силы относительно точки О – это вектор, модуль которого равен произведению силы на плечо.Линия действия силы – это направление, вдоль которого можно переносить точку приложения силы без изменения характера движения. Плечо силы – это перпендикуляр, опущенный от оси вращения на линию действия силы l = R∙sinα  (1)Модуль вектора момента силы равен  (2)Под действием момента сил тело приходит во вращательное движение и приобретает угловую скорость. Твердое тело может быть представлено как совокупность материальных точек, каждая из которых отстоит на ri от оси вращения. Угловая скорость одинакова для всех точек твердого тела и для каждой из них линейная скорость  . Наряду с моментом сил можно ввести понятие момента импульса каждой материальной точки твердого тела.Момент импульса относительно точки О – вектор, модуль которого равен произведению импульса тела на его плечо.   (3)Модуль момента импульса равен  (4) =>  Учитывая, что угловая скорость перпендикулярна радиусу,  , тогда (5)Момент инерции материальной точки – это величина, численно равная I=mR2. Для абсолютно твердого тела 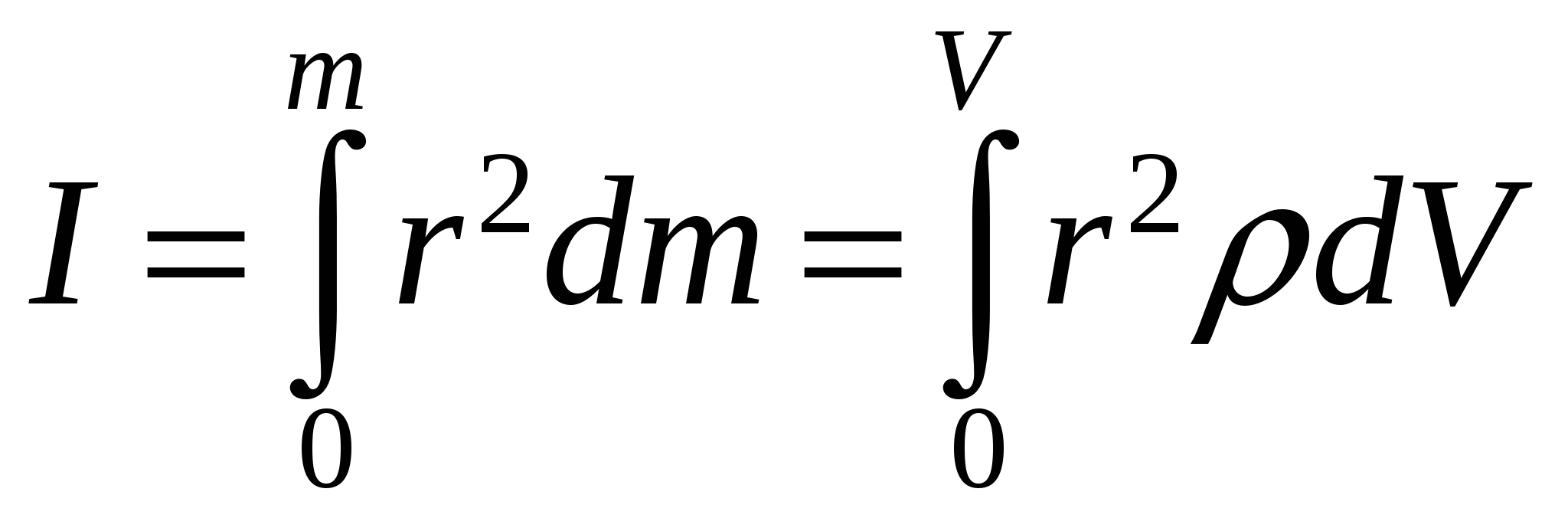 (6), или, для сплошных тел  , где r – это расстояние до оси вращения. Если известен момент инерции тела относительно его центра масс, то легко определить его момент инерции относительно произвольной оси, параллельной той, что проходит через центр масс. Выражение, позволяющее осуществить данный переход, носит название теоремы Штейнера  .Учитывая (5), получим  (7) – момент импульса твердого тела.Продифференцируем уравнение (4)  , или в векторном виде  (8)- уравнение моментов При равенстве нулю момента внешних сил момент импульса системы сохраняется. Условия равновесия твердого тела: 1)  - исключает ускоренное поступательное движение2)  - исключает ускоренное вращательное движение. |