Отс Лабораторная работа 1. Дискретизация сигналов. Спектр дискретного сигнала
 Скачать 187.54 Kb. Скачать 187.54 Kb.
|
|
Федеральное агентство связи Уральский технический институт связи и информатики (филиал) ФГБОУ ВО «Сибирский государственный университет телекоммуникаций и информатики» в г. Екатеринбурге (УрТИСИ СибГУТИ) Отчет по лабораторной работе №1 по дисциплине: Общая теория связи на тему: «Дискретизация сигналов. Спектр дискретного сигнала» Вариант №1. Выполнил: студент гр. ОЕ-81б Александрова А.М. Проверил: Глазырин Е.В. Екатеринбург 2021 1. Цель работы: Изучение алгоритмов дискретизации, прореживания и интерполяции сигналов, моделирование этих процессов, исследование спектра сигналов на входе и выходе дискретизатора. 2. Ответы на контрольные вопросы: Что такое дискретизация аналогового сигнала? Начертите временные диаграммы сигналов на входе и выходе дискретизатора. Начертите амплитудный спектр аналогового синусоидального колебания и спектр дискретной синусоиды в случае, когда частота синусоидального колебания меньше половины частоты дискретизации. Дискретизация – это замена непрерывного сигнала дискретными отсчетными значениями (отсчетами), взятыми через определенный интервал времени - интервал дискретизации TД. 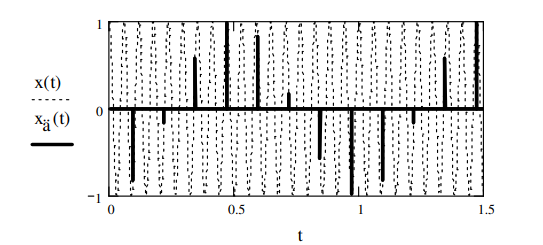 Рис. 1 – Временные диаграммы сигналов на входе и выходе дискретизатора  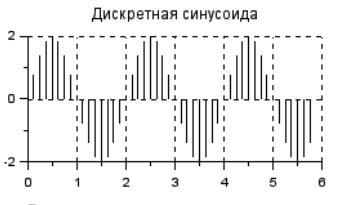 Рис. 2 – Амплитудный спектр аналогового синусоидального колебания и спектр дискретной синусоиды, F<Fd/2 Как определить амплитудный спектр на выходе дискретизатора, если спектр входного аналогового сигнала содержит несколько спектральных составляющих? Если спектр аналогового сигнала содержит не одну, а несколько спектральных составляющих, то каждая из них порождает в дискретном сиг-нале группу составляющих с амплитудами, пропорциональными своей амплитуде. Если из спектра дискретного сигнала выделить составляющие, соответствующие спектру исходного аналогового сигнала, то таким образом можно восстановить аналоговый сигнал из дискретного. Такую селекцию можно осуществить с помощью фильтра. Но реализовать такую фильтрацию можно только при выполнении условия 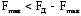 , ,где 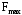 - максимальная частота спектра аналогового сигнала. - максимальная частота спектра аналогового сигнала.Из приведенного неравенства вытекает известное соотношение Котельникова, позволяющее выбрать частоту дискретизации  . .В чем сущность эффекта наложения спектров? Каким образом можно уменьшить ошибку наложения? Если дискретизация по времени вносит искажения в исходный сигнал, выражающиеся в том, что более верхние частоты суммируются с более низкими частотами, то в результате этого исходная форма спектра меняется. Этот эффект называется наложением спектров. Он влечет за собой частичную или полную потерю информации о исходном сигнале. После такой дискретизации исходный сигнал уже никогда не сможет быть восстановлен в полном объеме. В случае, когда нельзя по каким-либо причинам увеличить частоту дискретизации сигнала с ограниченным спектром, или аналоговый сигнал имеет неограниченный спектр, для уменьшения ошибки наложения спектров требуется предварительное ограничение спектра аналогового сигнала. Из рисунка 3 видно, что при этом ошибка наложения уменьшается в два раза.  Рис. 3 – Уменьшение ошибки наложения спектров при ограничении спектра аналогового сигнала Начертите амплитудный спектр дискретной синусоиды, если частота аналогового синусоидального колебания на входе дискретизатора выше частоты дискретизации.  Рис. 4 – Амплитудный спектр дискретной синусоиды,F>Fd/2 Из каких условий выбирается частота дискретизации модулированного колебания, если результатом последующей цифровой обработки должно быть выделение модулирующего колебания? 1) fВХ < fД/2. 2) fВХ = fД/2 3) fД/2 С какой целью осуществляется прореживание отсчетов дискретного сигнала? Поясните этот процесс с помощью временных диаграмм. Прореживание, как правило, выполняется в двух случаях. Во-первых, в многофункциональных устройствах, обеспечивающих обработку как высокочастотных, так и низкочастотных сигналов. При этом аппаратно частота дискретизации выбирается, исходя из требований к дискретизации сигналов с максимальной частотой, а при обработке низкочастотных сигналов она понижается за счет прореживания отсчетов. Во-вторых, прореживание можно осуществлять по мере сужения спектра сигнала за счет предварительной фильтрации. И в первом, и во втором случае прореживание увеличивает время обработки сигнала, а значит, позволяет реализовать более сложные алгоритмы обработки. На рисунке 5 показан фрагмент укрупненного алгоритма цифровой обработки с прореживанием отсчетов и временные диаграммы сигналов на входе и выходе прореживателя.  Рис. 5 – Фрагмент алгоритма цифровой обработки с прореживанием отсчетов и временные диаграммы сигналов на входе и выходе прореживателя. Этот фрагмент включает цифровой фильтр (ЦФ), прореживатель с коэффициентом прореживания М0 и блок последующей обработки сигнала (БО). Операция прореживания сводится к пропуску (М 0 - 1) отсчета исходного сигнала. Что такое интерполяция дискретного сигнала? Начертите временные диаграммы сигналов на входе и выходе интерполятора нулевого порядка. Объясните, почему однородный фильтр обеспечивает интерполяцию нулевого порядка. Интерполяцией называется процесс повышения частоты дискретизации. Интерполяция дискретного сигнала упрощает процесс последующего цифро-аналогового преобразования. 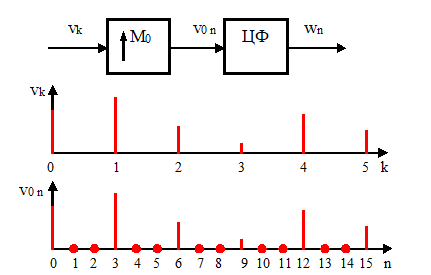 Рис. 6 – Интерполяция нулевого порядка В состав интерполятора входит блок повышения частоты дискретизации в М 0 раз и интерполирующий цифровой фильтр. Из временных диаграмм видно, что интерполяция осуществляется в два этапа: сначала вместо отсутствующих отсчетов сигнала 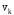 в сигнале в сигнале 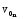 формируются нулевые отсчеты. Затем сигнал, содержащий нулевые отсчеты, подается на интерполирующий цифровой фильтр, восстанавливающий отсутствующие отсчеты. формируются нулевые отсчеты. Затем сигнал, содержащий нулевые отсчеты, подается на интерполирующий цифровой фильтр, восстанавливающий отсутствующие отсчеты. В интерполяторе нулевого порядка отсутствующие отсчеты принимают значение предшествующего им отсчета входного сигнала. Начертите временные диаграммы сигналов на входе и выходе интерполятора первого порядка (линейного интерполятора). Почему триангулярный фильтр обеспечивает линейную интерполяцию. 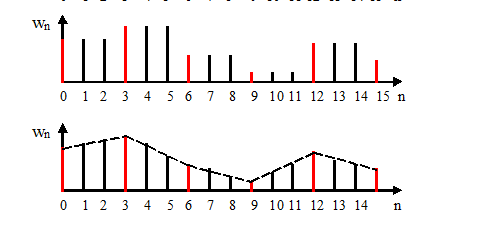 Рис. 7 – Интерполяция первого порядка В интерполяторе первого порядка вершины отсутствующих отсчетов находятся на прямой, которая соединяет вершины двух соседних отсчетов входного сигнала интерполятора. Интерполяция нулевого порядка осуществляется с использованием однородного цифрового фильтра, а для интерполяции первого порядка применяется триангулярный фильтр. 3. Выполнение заданий: 3.1 Сформируйте аналоговый сигнал в виде случайной последовательности элементарных посылок, где i – порядковый номер расчетной точки. Текущее время t связано с порядковым номером расчетной точки i следующим соотношением 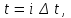 где 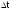 - временной интервал между двумя расчетными точками. - временной интервал между двумя расчетными точками.Минимальный уровень сигнала xi равен нулю, максимальный – Xmax, количество расчетных точек в одной элементарной посылке равно iv, максимальный номер расчетной точки равен imax. Значения этих параметров приведены в таблице 1. Пронаблюдайте амплитудный спектр этого сигнала. Таблица 1
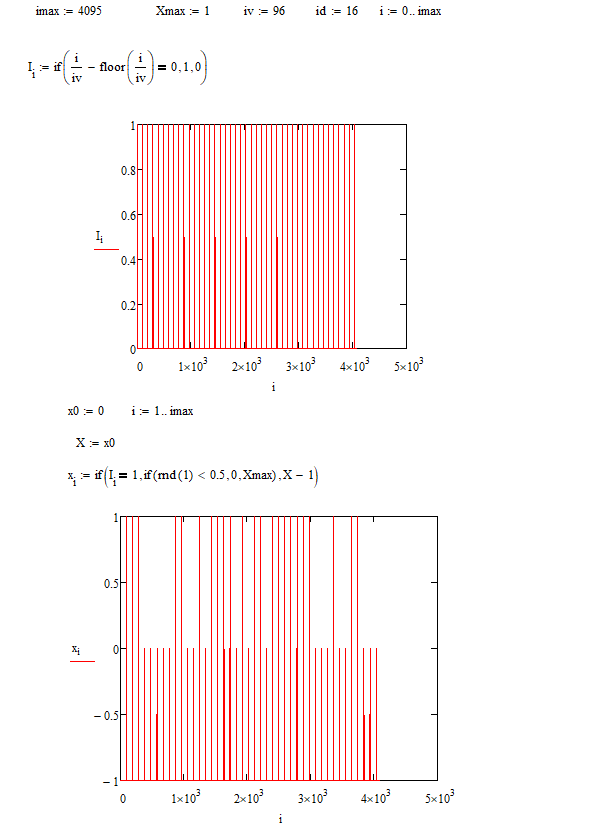 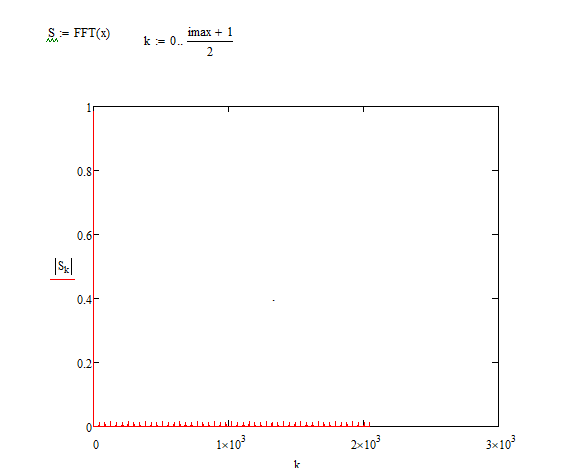 3.2 Выполните дискретизацию сформированного сигнала, приняв, что количество расчетных точек в интервале дискретизации равно id. Значение id возьмите из таблицы 1. Определите спектр дискретного сигнала. Обратите внимание на эффект размножения спектра. Повторите эксперимент при id в два раза большем, чем приведенном в таблице 1. Пронаблюдайте эффект наложения спектров 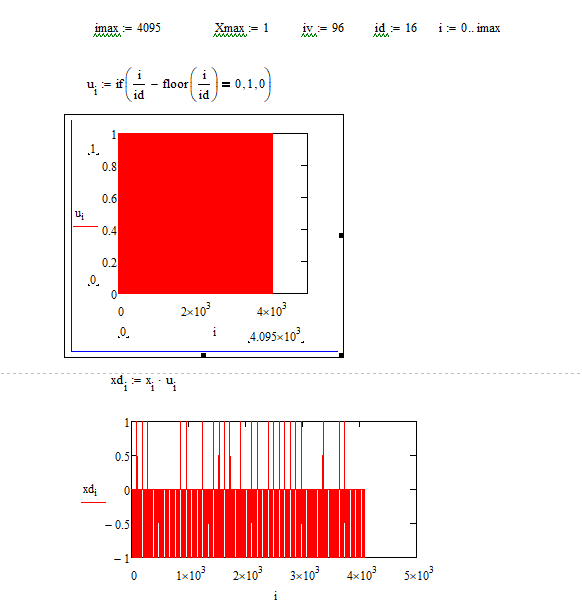  | |||||||||||||||||||||||||||||||||||||||||
