лекция. Лекция 4 (07.04.2020). Для понимания темы повторить основные логические функции, их формульный вид и таблицы истинности
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
Лекция 4 (7.04.2020) Законы и аксиомы алгебры логики Лекцию полностью перенести в конспект, внимательно разобрать все примеры!!! Для понимания темы повторить основные логические функции, их формульный вид и таблицы истинности (лекция 2)!!! 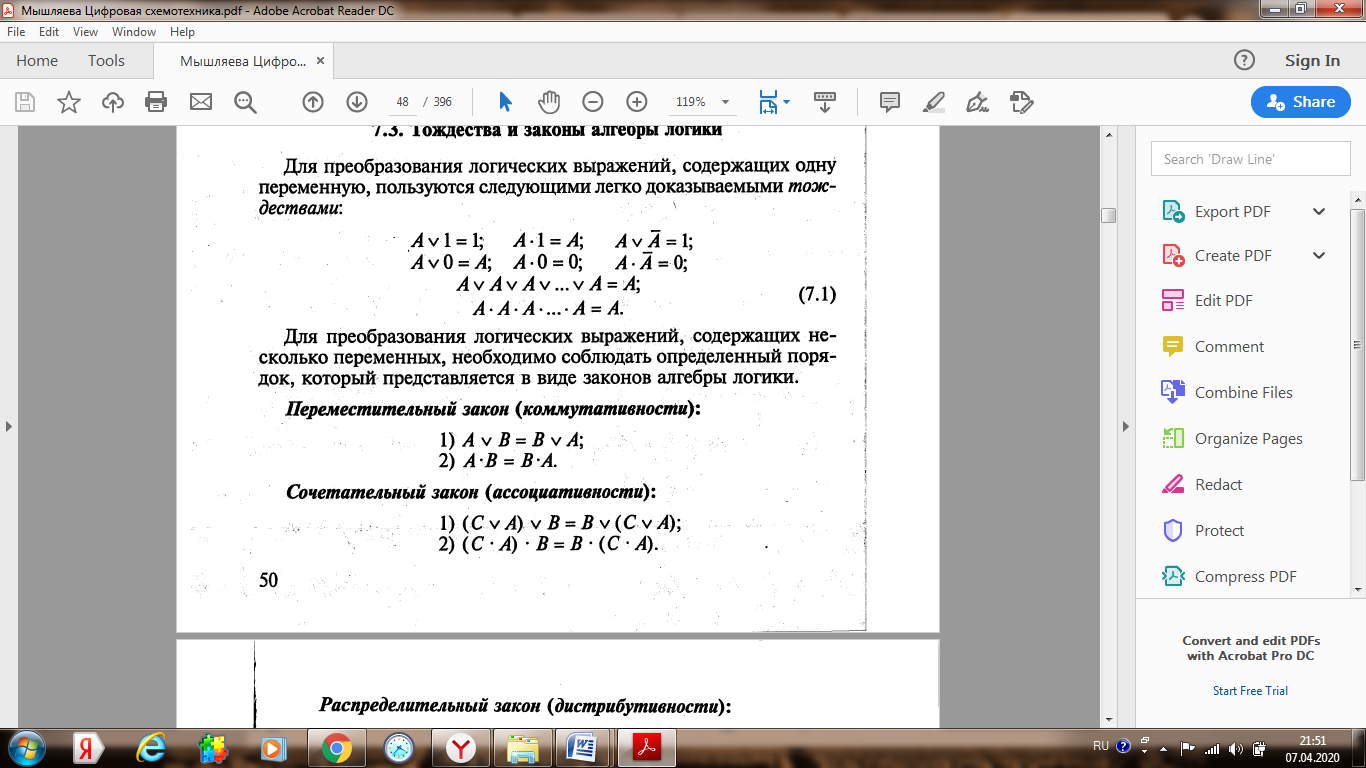 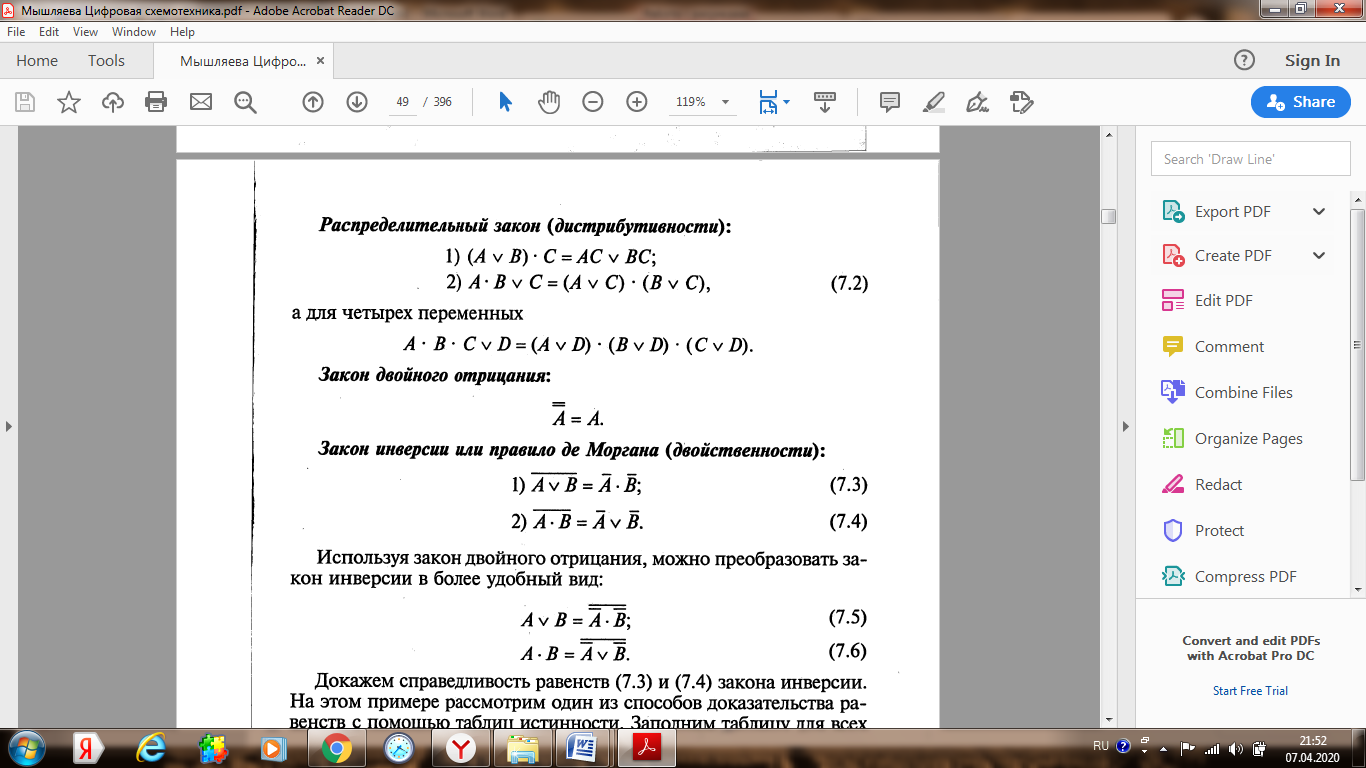 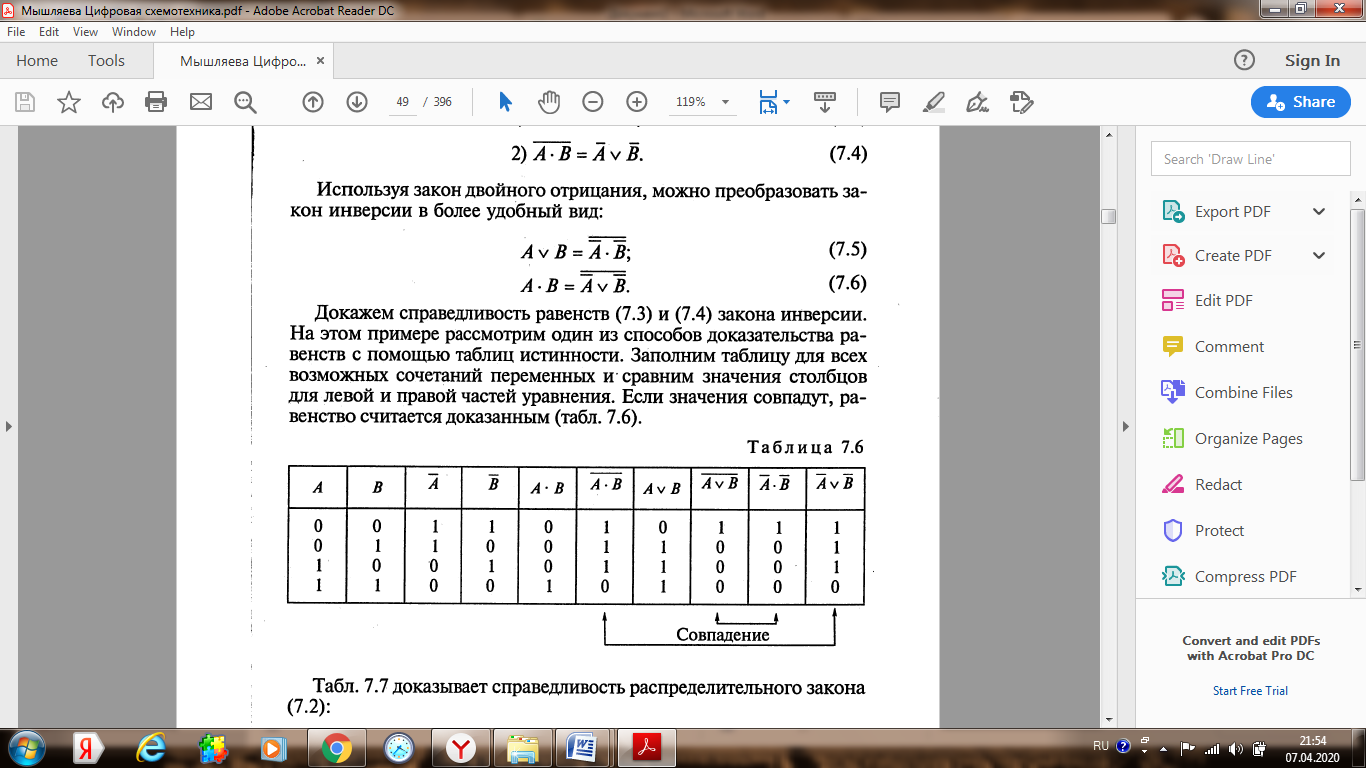 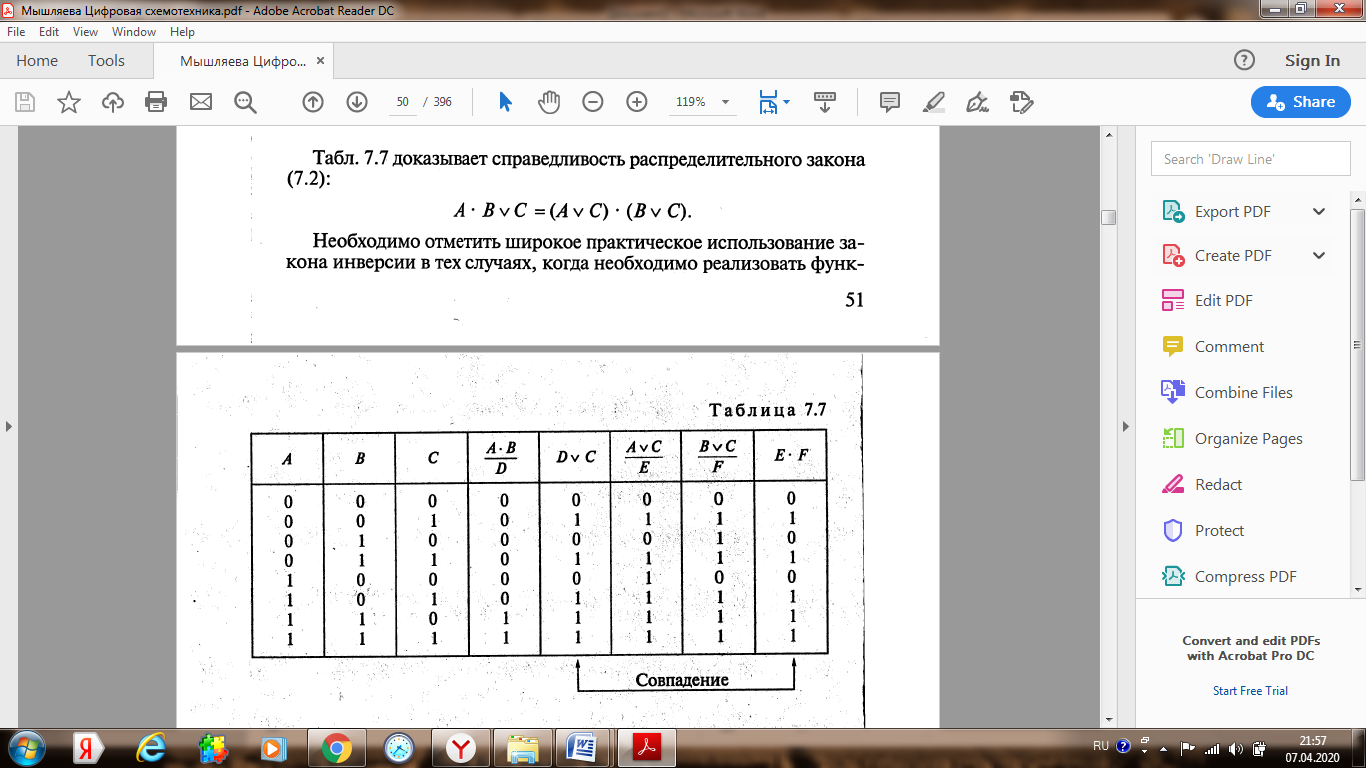 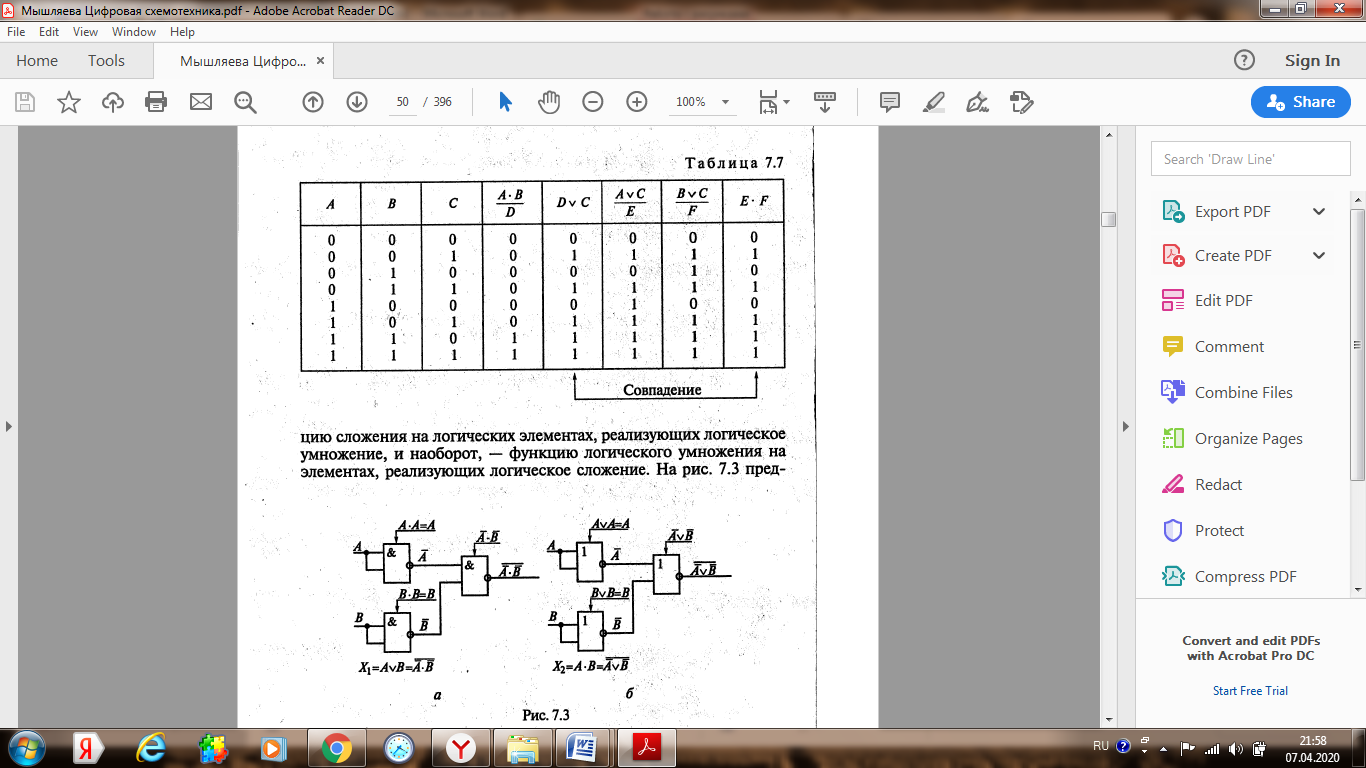 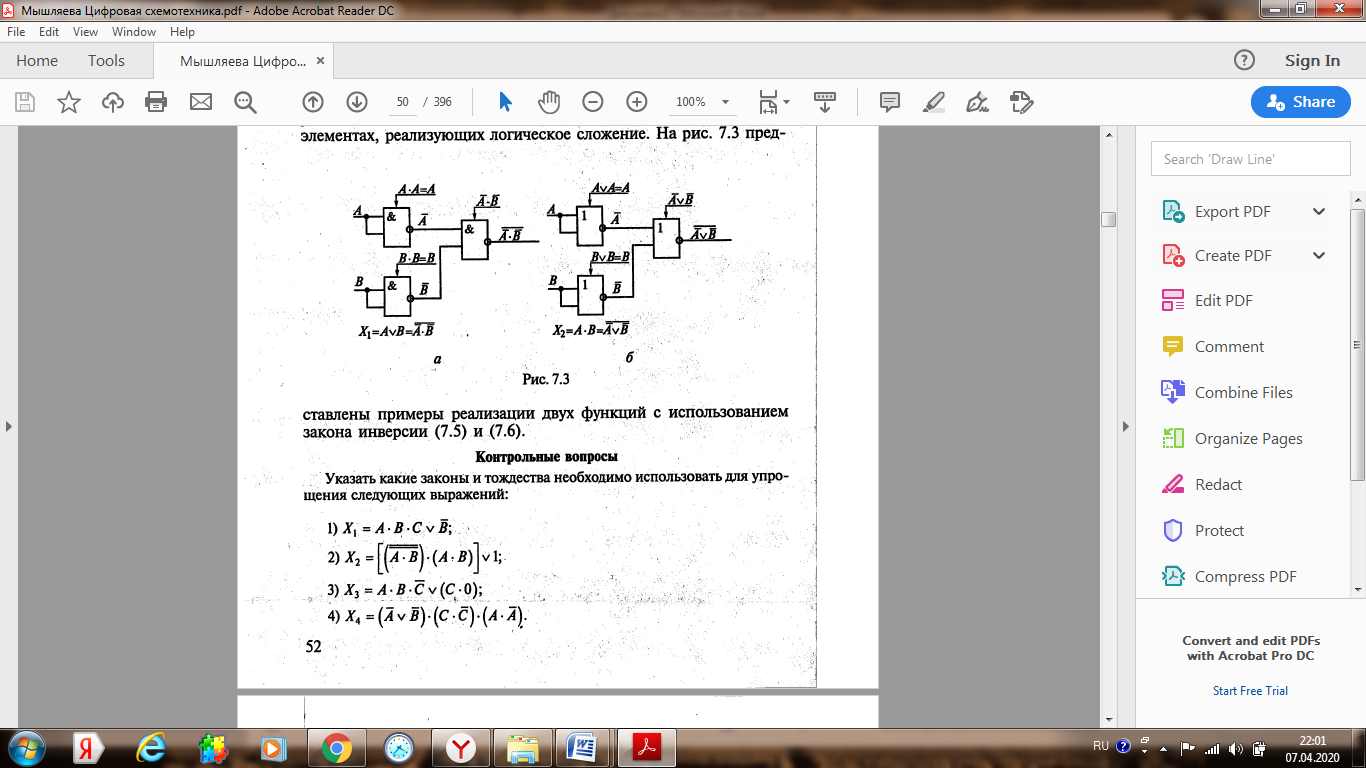 !!!! В рассмотренных ниже примерах логическое обозначение суммы v (дизъюнкция) заменяется знаком арифметической операции + Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул. В этом примере применены законы противоречия (11) и исключения констант (7). В этом примере применён закон противоречия (11) и определение операции «Логического сложения». В примере 3 применены законы противоречия (11) и исключения констант (7). В примере (4) применён закон противоречия (11) и определение операции «Логического умножения». Законы алгебры логики в этом примере применяются в следующей последовательности: правило де Моргана (14), сочетательный закон (6), закон противоречия (11) и правило операций с константами (7). Законы алгебры логики в этом примере применяется в таком порядке: правило де Моргана (14), выносится за скобки общий множитель (закон дистрибутивности (8)), закон противоречия (11). В этом примере к отрицаниям неэлементарных формул применяется правило де Моргана ((14) и (15)); сочетательный закон (6), используются законы двойного отрицания (13) и определение операции «Логического сложения». Часто для упрощения логических выражений применяют следующие тождества: Использование этих формул означает, что любое выражение можно умножить на единицу или к любому выражению добавить нуль. Пример: 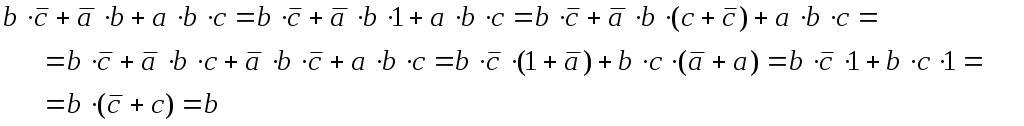 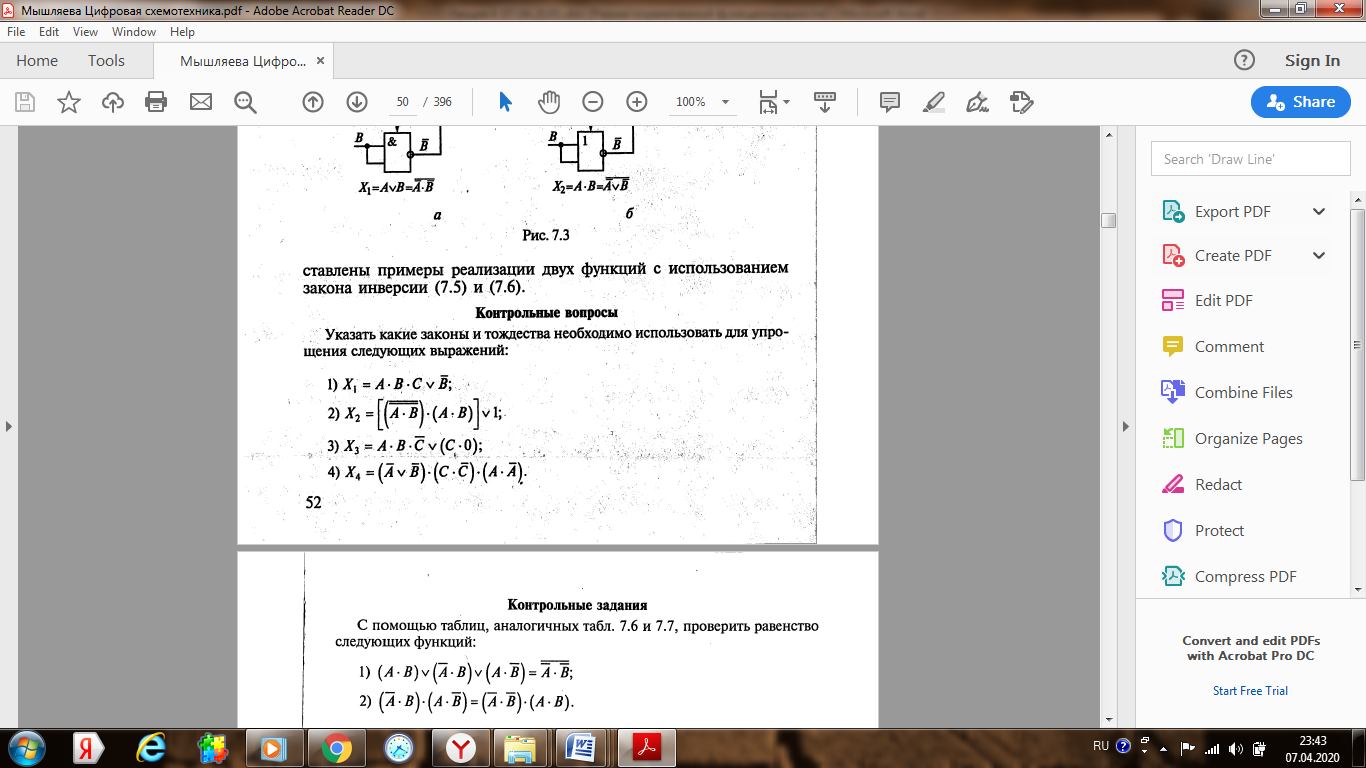 |
