Доклад. Доклад по теме Сложение колебаний

• Название: Доклад по теме Сложение колебаний
• Дата: 03.12.2020
• Размер: 94.51 Kb.
• Имя файла: Доклад.docx
• Тип: Доклад; #156544

Доклад по теме

«Сложение колебаний»

Колебанияминазываются движения или процессы, обладающие той или иной повторяемостью во времени.

Сло­жение нескольких гармонических колебаний одного направления и одинаковой частоты становится нагляд­ным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой .

Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x . Из взятой на оси точки О отложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угло­вой скоростью щ₀ , то проекция конца вектора будет перемещать­ся по оси x в пределах от —А до +A , причем координата этой проекции будет изменяться со временем по закону





Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с ам­плитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с на­чальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.

Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого рав­на амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.

Рассмотрим сложение двух гармонических коле­баний одного направления и одинаковой частоты. Результирующее колебаниебудет суммой колеба­ний х₁и x₂ , которые определяются функциями

,  (1)

Представим оба колебания с помощью векторов A₁и А₂. Построим по правилам сложения векторов результирующий вектор А. На рисунке вид­но, что проекция этого вектора на ось x равна сум­ме проекций складываемых векторов: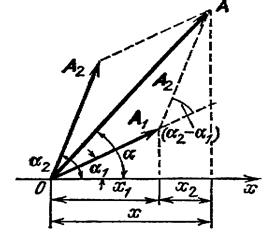



Поэтому, вектор Aпредставляет собой резуль­тирующее колебание. Этот вектор вращается с той же угловой скоростью щ₀ , как и векторы А₁и А₂, так что сумма x₁и х₂является гармоническим колебанием с частотой (щ₀ , амплитудой A и начальной фа­зой б. Используя теорему косинусов получаем, что

(2)

Также, из рисунка видно, что

(3)

Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.

Сложение колебаний во взаимно перпендикулярных направлениях.

Представим две взаимно перпен­дикулярные векторные величины xи y, изменяющие­ся со временем с одинаковой частотой щ по гармони­ческому закону, то

 (1)

Где e_xи e_у— орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия.

В случае колеблющейся частицы величины

,   (2)

определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от раз­ности фаз обоих колебаний. Выражения (2) пред­ставляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравне­ние траектории в обычном виде, нужно исключить из уравнений (2) параметр t. Из первого уравне­ния следует, что

 (3) Соответственно   (4)

Развернем косинус во втором из уравнений (2) по формуле для косинуса суммы:



Подставим вместо cos щ t и sinщt их значения (3) и (4):





Преобразуем это уравнение







 (5)

Это уравнение эллипса, оси которого по­вернуты относительно координатных осей х и у. Ори­ентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз б.

Попробуем найти форму траектории для нескольких частных случаев.

1. Разность фаз б равна нулю. В этом случае уравнение (5) упрощается следующим образом:



Отсюда получается уравнение прямой:



Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой щ и ам­плитудой, равной   (рис. 1 а).

2. Разность фаз б равна ±р. Из уравнение (5)имеет вид



Следовательно, результирующее движение представ­ляет собой гармоническое колебание вдоль прямой

 (рис. 1 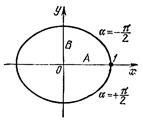б)



Рис.1

3. При   уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:



Полуоси эллипса равны соответствующим амплиту­дам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.

Случаи  и  отличаются на­правлением движения по эллипсу или окружности.

Следовательно, равномерное движение по окружности радиуса R с угловой скоростью щ может быть представлено как сумма двух взаимно перпен­дикулярных колебаний:

, 

(знак плюс в выражении для у соответствует движе­нию против часовой стрелки, знак минус — движе­нию по часовой стрелке).

Если частоты взаимно перпендикулярных колеба­ний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, на­зываемых фигурами Лиссажу.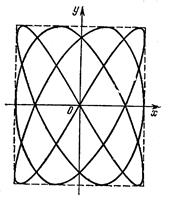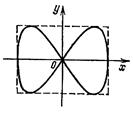