Домашнее задание Расчет механических и скоростных характеристик асинхронного короткозамкнутого электродвигателя Порядок выполнения и оформления расчетнографических работ
 Скачать 4.52 Mb. Скачать 4.52 Mb.
|
|
Домашнее задание № 4. Расчет механических и скоростных характеристик асинхронного короткозамкнутого электродвигателя Порядок выполнения и оформления расчетно-графических работ Расчетно-графические работы по курсу «Электротехника и электроника» способствуют закреплению теоретических знаний и практических навыков полученных при изучении учебников и выполнении лабораторных работ. Для успешного выполнения расчетно-графических работ необходимо: 1. Изучить соответствующие разделы учебников и учебных пособий. 2. Изучить методические указания к выполнению расчетно-графической работы. 3. Разобрать типовые примеры, приведенные в учебниках и методическом пособии по теме расчетно-графической работы. Расчетно-графические работы выполняются индивидуально каждым студентом. Номер варианта расчетно-графической работы соответствует номеру фамилии студента по списку в групповом журнале. Расчетно-графическая работа выполняется на листах формата А4 на одной стороне листа. Титульный лист оформляется в соответствии с общепринятой формой. Исходные данные приводятся на первой странице расчёт. Расчёт сопровождается пояснительными надписями. Все схемы, графики и диаграммы вычерчиваются аккуратно, по линейке, в выбранном для каждой физической величины в соответствии с ГОСТ масштабе. При оформлении работы приводятся все необходимые формулы, а также расчеты с подстановкой данных. При расчёте механических и рабочих характеристик электродвигателей допускается представление результатов в виде таблиц с подстановкой данных в формулы при вычислении только характерных режимов. Выполненная расчетно-графическая работа сдается преподавателю на проверку. После проверки и получения подписи преподавателя о допуске к защите, студент защищает расчетно-графическую работу, при защите расчетно-графической работы студенту даются вопросы, требующие знания методики проводимых расчетов и умения проведения анализа полученных результатов. Расчет характеристик трёхфазного асинхронного двигателя Расчетно-графическая работа представляет собой расчет естественной и искусственных механических характеристик и рабочих характеристик трёхфазного асинхронного двигателя серии 4А. При выполнении его необходимо: 1. Начертить Г-образную схему замещения асинхронного двигателя. 2. Рассчитать и построить естественные механические характеристики асинхронного двигателя M = f(s) и n2 = f(M). 3. Рассчитать и построить искусственные механические характеристики асинхронного двигателя n2 = f(M) при изменении: 1) Напряжения питания U1. 2) Активного сопротивления обмотки ротора R2’. 3) Частоты f1и напряжения питания U1 по закону U1/f1 = const. 4. Для естественного режима работы асинхронного двигателя рассчитать и построить его рабочие характеристики M, n2, I1, cos φ, P1, ƞ = f(P2) 5. Для заданного момента нагрузки MC асинхронного двигателя определить его основные энергетические показатели I1, cos φ, P1, ƞ при номинальном и пониженном напряжении питания. Рассчитать пусковые токи асинхронного двигателя при номинальном и пониженном напряжении питания. Сделать выводы о целесообразности регулирования напряжения питания электродвигателя. Исходными данными расчёта характеристик асинхронного двигателя являются приведённые в табл. 1. а) тип и паспортные данные электродвигателя: U1H – номинальное фазное напряжение, В; f1H – номинальная частота сети, Гц; P2H – номинальная мощность, кВт; n2H – номинальная частота вращения, мин-1; ƞH – коэффициент полезного действия электродвигателя в номинальном режиме, %; cos φH – коэффициент мощности электродвигателя в номинальном режиме; б) параметры схемы замещения: Rx, Xx – активное и индуктивное сопротивления цепи намагничивания электродвигателя, Ом; R1, X1 – активное и индуктивное сопротивления фазной обмотки статора, Ом; R2’, X2’ – приведённые к обмотке статора активное и индуктивное сопротивления фазной обмотки ротора, Ом; в) коэффициенты, задающие степень изменения параметров электрической сети и электродвигателя (сообщаются преподавателем): kU = U1/U1H – коэффициент относительного изменения напряжения питания электродвигателя; kR2 = R2H’/R2’ – коэффициент относительного изменения приведённого активного сопротивления фазной обмотки ротора; kf = f1/f1H – коэффициент относительного изменения частоты напряжения питания. Дополнительную информацию об электродвигателе можно получить из его условного обозначения, структура которого поясняется на примере асинхронного двигателя 4A160S4УЗ, где: З – условное обозначение категории размещения электродвигателя (З – исполнение электродвигателя для эксплуатации в закрытых помещениях с естественной вентиляцией без искусственно регулируемых климатических условий); У – условное обозначение климатического исполнения электродвигателя (У – электродвигатели, предназначенные для эксплуатации в районах с умеренным климатом); 4 – число полюсов 2р электродвигателя; S – условное обозначение установочного размера по длине станины (S – меньший, М – средний, L – большой) и длины сердечника (А – меньшая, В – большая); 160 – высота оси вращения (вала) от основания станины, мм; 4А – название серии (четвёртая серия асинхронных двигателей). Основные теоретические положения и методические указания к выполнению расчетно-графической работы 4.1. Устройство и схема замещения асинхронного двигателя Трехфазный асинхронный двигатель состоит из двух основных частей: неподвижного статора и вращающегося ротора.  Рис. 1 Статор (рис. 1) представляет собой помещенный внутри встального или алюминиевого корпуса 1 полый цилиндр 2, собранный из кольцеобразных изолированных пластин электротехнической стали. На его внутренней стороне имеются пазы, в которых размещаются симметрично три фазные обмотки 3, состоящие из одной или нескольких катушек медного изолированного провода. Фазные обмотки соединяются звездой или треугольником и подключаются к трехфазной сети. Схема соединения фазных обмоток зависит от линейных напряжений трехфазной сети, указанных на щитке электродвигателя, например, 220/380 В. При меньшем напряжении 220 В фазные обмотки соединяются треугольником, а при большем напряжении 380 В звездой, что обеспечивает при каждом способе соединения фазное напряжение обмоток 220 В. Ротор асинхронного двигателя представляет собой закрепленный на валу цилиндр, собранный из изолированных пластин электротехнической стали, на внешней стороне которого имеются пазы. В пазах расположена его обмотка, которая может быть короткозамкнутой и фазной. Соответственно различают асинхронный двигатель с короткозамкнутым и фазным ротором.  Рис. 2  Рис. 3 Обмотка короткозамкнутого ротора (рис. 2) выполняется в виде круглой («беличьей») клетки, образованной расположенными в пазах ротора медными или алюминиевыми стержнями 1, замкнутыми накоротко с двух сторон кольцами 2 из того же материала. Фазная обмотка ротора (рис. 3) выполняется так же, как и обмотка статора, изолированным медным проводом. Ее катушки соединяются звездой, а их свободные концы присоединяются к контактным кольцам 1, находящимся на валу ротора. Кольца изолированы друг от друга и от вала. К контактным кольцам прижаты графитовые щетки 2, при помощи которых к обмотке ротора подключается трехфазный реостат 3. Его включение в цепь обмотки ротора позволяет регулировать частоту вращения асинхронного двигателя, а также существенно улучшить его пусковые свойства, т.е. уменьшить пусковой ток и одновременно увеличить пусковой момент. Ротор асинхронного двигателя помещается внутри статора и фиксируется в этом положении при помощи боковых подшипников щитов.  Рис. 4 Для анализа характеристик асинхронного двигателя в установившихся режимах пользуются его электрической схемой замещения. На рис. 4 изображена Г – образная схема замещения асинхронного двигателя. Она представляет собой составленную из идеализированных элементов электрическую схему замещения одной фазы электродвигателя, в которой магнитная связь между статором и ротором заменена электрической. По аналогии со схемой замещения трансформатора переменный резистор R2’(1 – s)/s представляет в ней эквивалент полезной нагрузки. Поэтому мощность, выделяемая в нем, будет равна одной трети механической мощности Pмех, развиваемой асинхронным двигателем. По схеме замещения можно определить мощность потерь в стали ΔРст мощности потерь в обмотках статора ΔРэ1и ротора ΔРэ2 , а также потребляемую асинхронным двигателем мощность Р1. 4.2. Естественные механические характеристики асинхронного двигателя Механической характеристикой асинхронного двигателя называется зависимость развиваемого им момента от скольжения M = f(s) и зависимость частоты вращения ротора от развиваемого момента n2 = f(M). Механическая характеристика двигателя, полученная при номинальных (паспортных) напряжении и частоте сети при основной схеме включения его обмоток без включенных в их цепи дополнительных электротехнических элементов, является естественной. Если указанные условия не соблюдаются, то механическая характеристика будет искусственная. Расчёт естественной механической характеристики асинхронного двигателя выполняется по формуле, представляющей собой аналитическую зависимость его электромагнитного момента от скольжения: 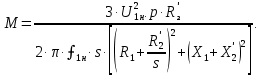 где p – число пар полюсов обмотки статора. Механическая характеристика асинхронного двигателя нелинейная, поэтому при выполнении этого пункта задания рекомендуется задаться значениями скольжения s = 0; 0,5sH; sH; 1,5sH; sK; 0,6; 0,8; 1,0 и определить соответствующий им электромагнитный момент. Скольжению s = 0 соответствует режим идеального холостого хода электродвигателя‚ при работе в котором его частота вращения равна частоте вращения магнитного поля, т.е. синхронной частоте вращения: 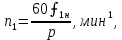 а электромагнитный момент равен М = 0. Скольжение асинхронного двигателя рассчитывается по формуле: 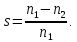 При расчёте номинального скольжения электродвигателя в ней принимается n2 = n2H. Критическое скольжение, при котором асинхронный двигатель развивает максимальный момент MK, зависит от параметров его обмоток: 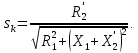 Значению s = 1 соответствует пусковой режим электродвигателя, при котором его частота вращения равна n2 = 0, а развиваемый электромагнитный момент называется пусковым моментом Мп. Построение механической характеристики n2 = f(М) производится по данным, полученным при расчёте зависимости М = f(S) с помощью следующего соотношения: n2 = n1(1 – s). Примерный вид естественных механических характеристик асинхронного двигателя с указанием характерных точек показан на рис. 5‚ 6. При оформлении домашнего задания они строятся совместно с искусственными механическими характеристиками.  Р 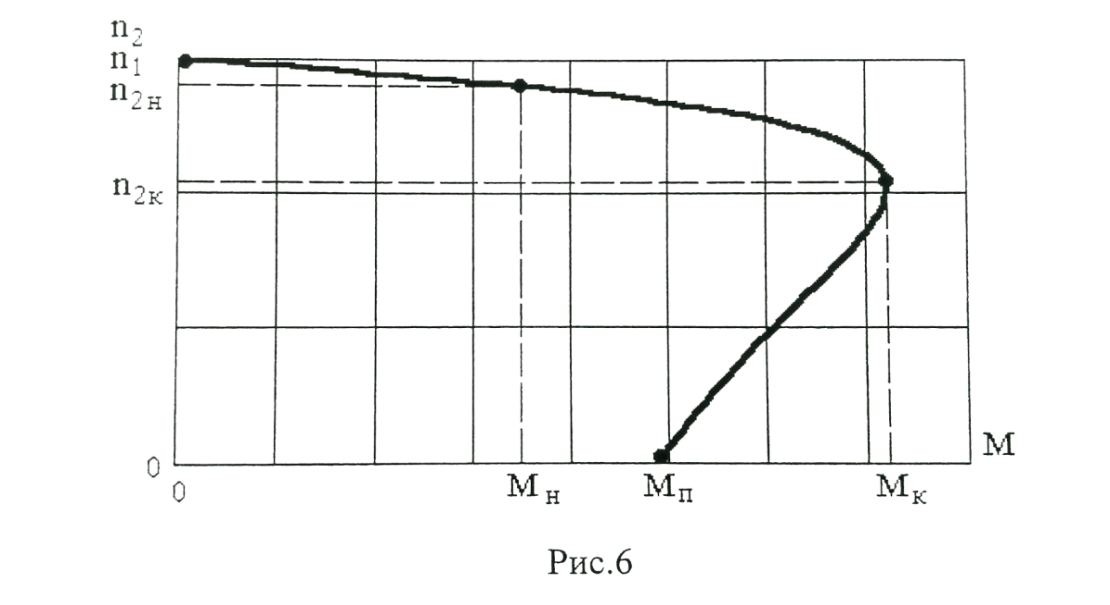 ис. 5 Рис. 6 3. Искусственные механические характеристики асинхронного двигателя Особенности расчёта искусственных механических характеристик асинхронного двигателя состоят в следующем. 3.1. При изменении напряжения питания критическое скольжение и соответствующая ему частота вращения асинхронного двигателя остаются такими же, как при его работе в естественном режиме. Электромагнитный момент асинхронного двигателя, как следует из его математического выражения, прямо пропорционален напряжению питания во второй степени. Поэтому его значения М для построения искусственной механической характеристики можно определить по результатам расчёта естественной механической характеристики п.2 задания, используя следующее соотношение: 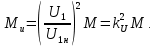 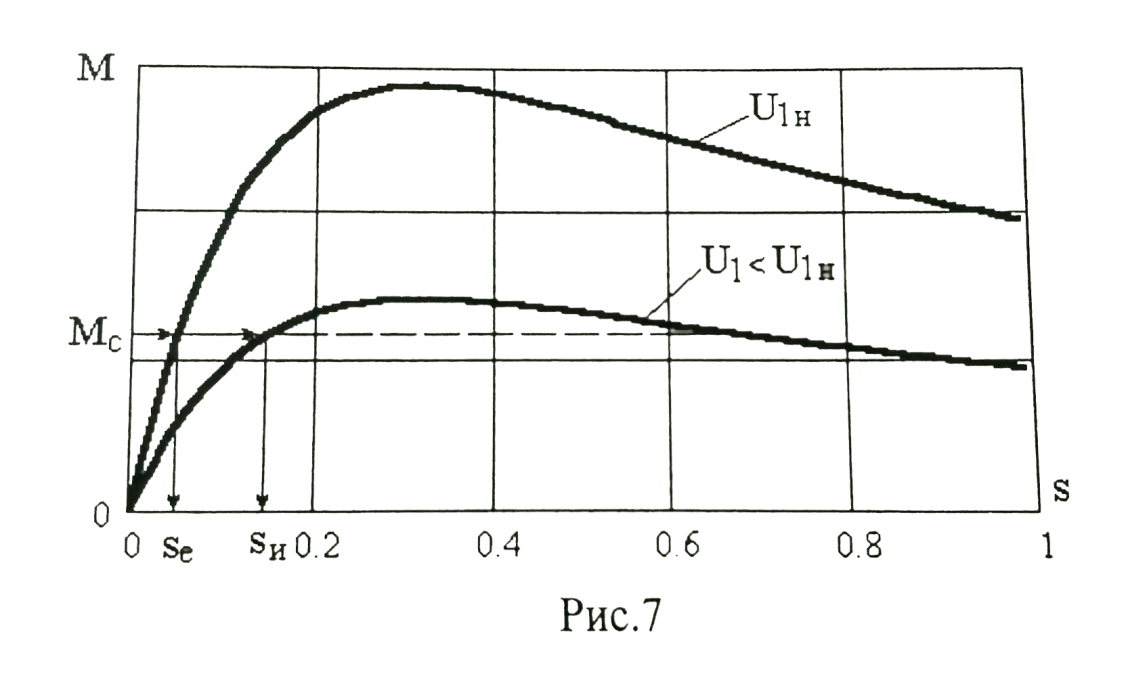 Рис. 7 Р 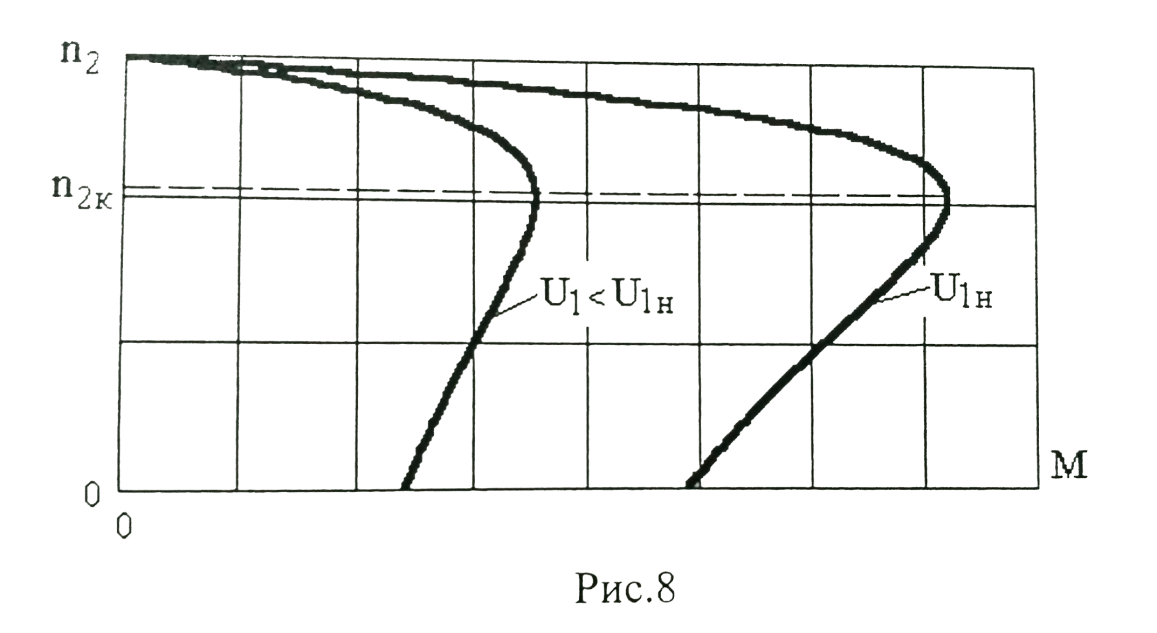 ис. 8 Механические характеристики при изменении напряжения питания асинхронного двигателя изображены на рис. 7, 8. 3.2. Увеличение активного сопротивления фазной обмотки ротора асинхронного двигателя до R2и’= kR2R2' приводит к пропорциональному возрастанию критического скольжения: 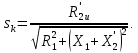 Электромагнитный момент двигателя при измененном активном сопротивлении обмотки ротора рассчитывается по формуле: 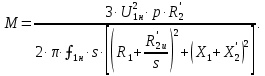 П 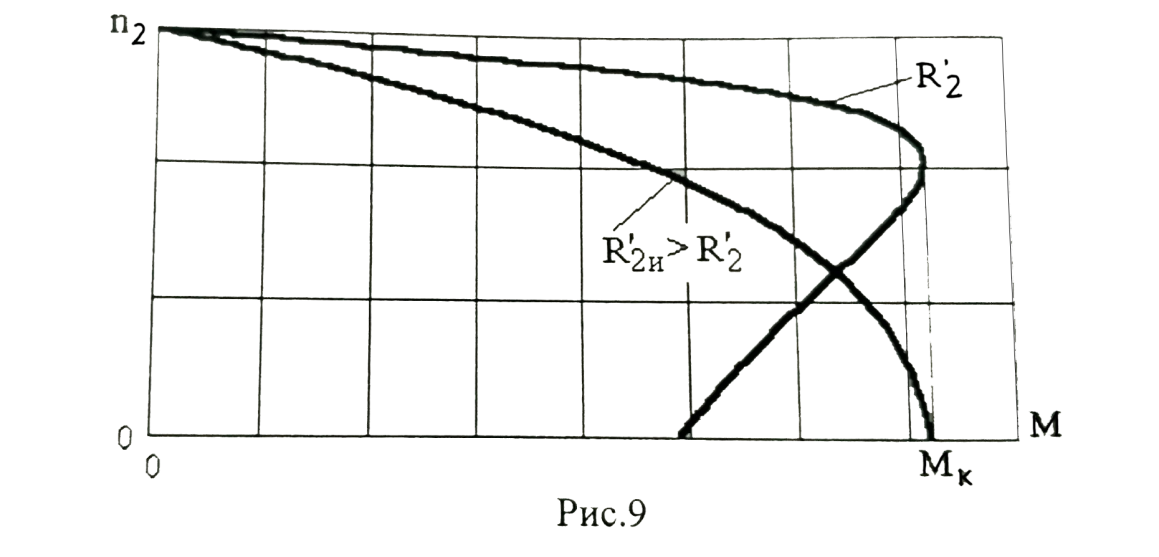 ри расчете этой искусственной механической характеристики рекомендуется задаться значениями скольжения s = 0; sн; 4sн; sки; 0,6; 0,8; 1,0. Влияние активного сопротивления фазных обмоток ротора на механическую характеристику асинхронного двигателя показано на рис. 9. Рис. 9 3.3. При регулировании частоты вращения асинхронного двигателя изменением частоты напряжения питания по закону U1/f1 = const его критическое скольжение находится из следующего выражения: 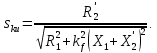 Т.е. с уменьшением частоты питающего напряжения критическое скольжение возрастает, а с увеличением частоты уменьшается. Расчет электромагнитного момента двигателя производится с учетом того, что при рассматриваемом способе его регулирования 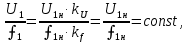 т.е. ku = kf на основании этого выражение для электромагнитного момента асинхронного двигателя принимает следующий вид: 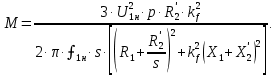 При расчете этой искусственной механической характеристики электронного двигателя рекомендуется задаться значениями скольжения s = 0; sн; 1,5sн; sкн; 0,6; 0,8; 1,0. Частота вращения магнитного поля в двигателе зависит от частоты напряжения питания и будет равна: 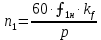 , ,а частота вращения его ротора 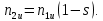 Механические характеристики асинхронного двигателя при рассматриваемом способе регулирования его частоты вращения изображены на рис. 10.  Рис. 10 4. Рабочие характеристики асинхронного двигателя Рабочими характеристиками асинхронного двигателя называется графические изображения зависимостей n2, M, I1, cos φ, P1, n = f(P2) при U1 = const и f1 = const. При U1 = U1н и f1 = f1н эти характеристики являются естественными. Расчет естественных рабочих характеристик асинхронного двигателя рекомендуется выполнить для значений скольжения s = sх; 0,5sн; sн; 1,5sн. При этом следует учесть, что соответствующие этим скольжениям значения электромагнитного момента М и частоты вращения n2 асинхронного двигателя, кроме значений этих параметров при его холостом ходе с s = sх, были рассчитаны ранее, в п.2 задания. Для определения значений других величин, входящих в состав рабочих характеристик двигателя, необходимо воспользоваться его Г-образной схемой замещения, изображенной на рис. 4. На основании первого закона Кирхгофа для этой схемы: 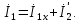 Токи в параллельных ветвях схемы замещения асинхронного двигателя рассчитываются по формулам: 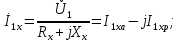 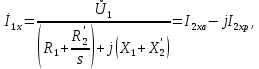 где I1ха, I1хр – активная и реактивная составляющие тока цепи намагничивания т.е. тока идеального холостого хода электродвигателя; 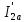 , , 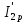 – приведенные к обмотке статора активная и реактивная составляющие тока обмотки ротора электродвигателя. В итоге фазный ток асинхронного двигателя будет равен: – приведенные к обмотке статора активная и реактивная составляющие тока обмотки ротора электродвигателя. В итоге фазный ток асинхронного двигателя будет равен: 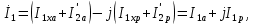 а его действующее значение: 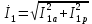 . .Коэффициент мощности асинхронного двигателя может быть определен по формуле: 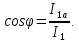 П 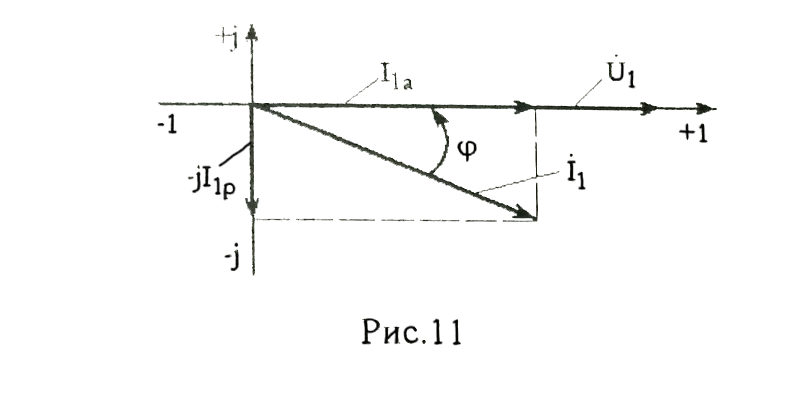 равомерность применения этой формулы для расчета cos φ асинхронного двигателя поясняет векторная диаграмма фазных напряжения и тока на рис. 11. Рис. 11 Потребляема двигателем из сети мощность рассчитывается по формуле: 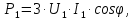 а развиваемая им механическая мощность на основании схемы замещения будет равна 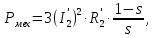 где 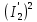 = = 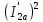 + + 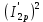 . . Для расчета коэффициента полезного действия (КПД) двигателя используется выражение: 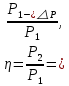 где P2 – полезная механическая мощность на валу двигателя; ΔP – мощность потерь в двигателе. Потери мощности ΔP, возникающие в асинхронном двигателе при преобразовании электрической энергии в механическую, рассеиваются в нем и вызывают его нагрев. Они состоят из двух состоящих: 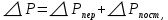 где ΔPпер – переменные потери мощности в двигателе; ΔPпост – постоянные потери мощности в двигателе. Переменные потери мощности зависят от нагрузки двигателя, т.е. от тока двигателя. В них входят мощность потерь в обмотке статора ΔPэ1, мощность потерь в обмотке ротора ΔPэ2 и мощность добавочных потерь ΔPд: 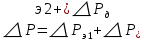 . .Из схемы замещения асинхронного двигателя (рис. 4) следует: 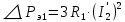 ; ;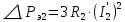 . .Добавочные потери мощности ΔPд возникают в обмотках двигателя и обусловлены зубчатостью статора и ротора, а также несинусоидальным распределением магнитной индукции в воздушном зазоре двигателя. Эти потери мощности пропорциональны квадрату фазного тока двигателя и составляют 0,5 – 2 % от номинальной мощности потерь ΔPд поэтому ими при расчете КПД асинхронного двигателя допустимо пренебречь. К постоянным потерям мощности асинхронного двигателя, не изменяющимся от нагрузки, при U1 = U1н и f1 = f1н можно отнести мощность потерь в стали ΔPст и мощность механических потерь ΔPмех. Общая мощность этого вида потерь будет равна: 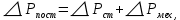 . .Мощность ΔPст определяется в основном потерями из-за гистерезиса и вихревых токов в сердечнике статора, так как подобные потери мощности в сердечнике ротора в связи с малой частотой тока обмотки ротора f2 = 1 – 3 Гц рабочем режиме асинхронного двигателя пренебрежимо малы. Тогда на основании схемы замещения (рис. 4) асинхронного двигателя 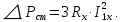 Мощность механических потерь ΔPмех обусловлена силами трения в подшипниках, ротора о воздух и вентиляционными потерями. Она определяется при номинальном режиме работы асинхронного двигателя. Для этого по вышеприведенным формулам при U1 = U1н и s = sн с использованием параметров схемы замещения асинхронного двигателя в следующей последовательности рассчитываются I1х, I’2н, ΔPэ2н и ΔPст, затем по паспортным данным определяется номинальная потребляемая мощность асинхронного электродвигателя: 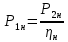 , ,и номинальную мощность потерь 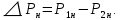 В результате мощность механических потерь будет равна: 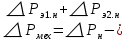 + +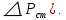 Полезная механическая мощность двигателя Р2 меньше развиваемой механической мощности Pмех на величину мощности механических потерь: 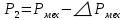 . .Механическим потерями мощности ΔPмех в двигателе соответствует приложенный к его валу момент трения: 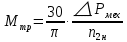 . .Для преодоления момента трения Мтр асинхронный двигатель должен развивать равный ему электромагнитный момент. Поэтому скольжение асинхронного двигателя при работе в режиме реального холостого хода sх меньше 0. Значение скольжения sх, принимая во внимание, что при 0 ≤ М ≤ Мн зависимость скольжения асинхронного двигателя от его электромагнитного момента практически линейная, можно определить из соотношения: 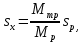 где sр, Мр – скольжение и соответствующий ему электромагнитный момент асинхронного двигателя в опорной точке механической характеристики. Выбор значения скольжения sр, по которому рассчитывается момент Мр, осуществляется в диапазоне 0,1sн ≤ sр ≤ 0,5sн. При этом следует учесть, что меньшему значению sр соответствует более высокая точность расчета sх. 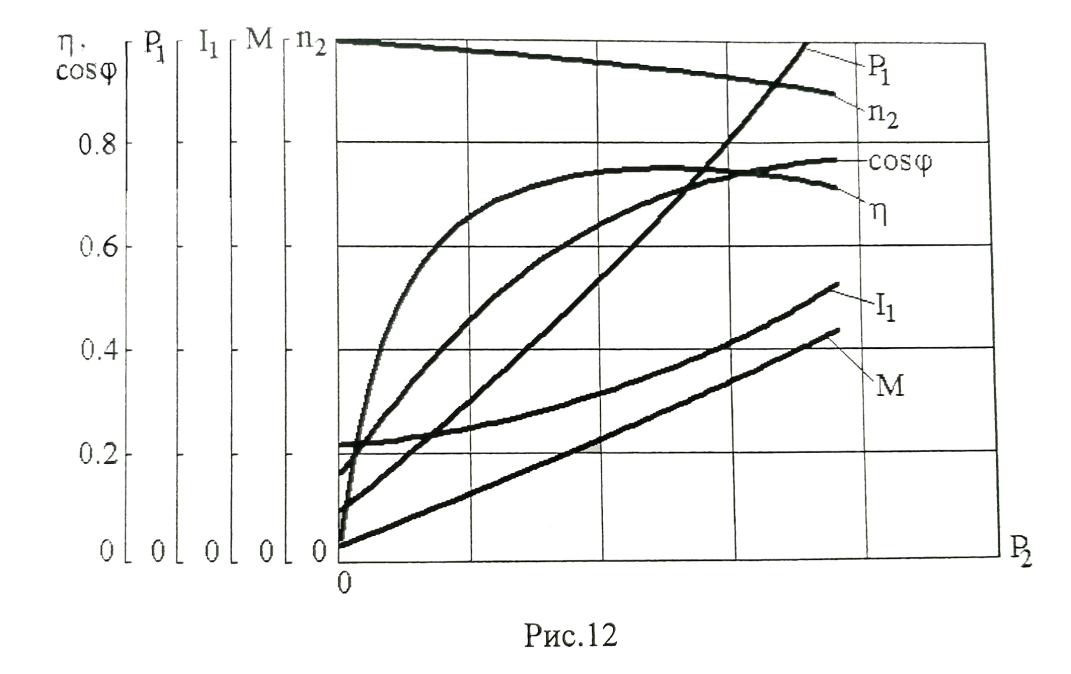 Рис. 12 По полученным данным строятся графики, отражающие зависимости изменения рассчитанных показателей асинхронного двигателя от развиваемой им мощности Р2. Их примерный вид показан на рис. 12. Из графиков рабочих характеристик асинхронного двигателя следует, что с увеличением нагрузки потребляемый им ток I1 возрастает. Увеличиваются также его коэффициент мощности cos φ и КПД. Эти показатели асинхронного двигателя имеют максимум, который у коэффициента мощности cos φ достигается при Р2 = Р2н. Максимальное значение КПД асинхронного двигателя, как и у трансформатора, при ΔPпост = ΔPпер. Это условие у асинхронных двигателей выполняется при нагрузках Р2 = (0,65 – 0,85)Р2н. |
