Матема. Домашнее задание 4 Случайная величина имеет следующее распределение
 Скачать 17.34 Kb. Скачать 17.34 Kb.
|
|
Домашнее задание 4 Случайная величина 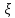 имеет следующее распределение: имеет следующее распределение:
Найти а) математическое ожидание и дисперсию 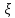 ; б) вероятность того, что ; б) вероятность того, что 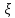 примет значение на отрезке [-0,5;0,5]. примет значение на отрезке [-0,5;0,5].Два студента независимо друг от друга решают задачу по теории вероятностей. Вероятность решить задачу для первого студента 0,75, для второго 0,8. Рассматриваются две случайные величины 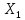 – количество решенных задач для первого студента, – количество решенных задач для первого студента, 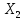 – количество решенных задач для второго студента. Так же исследуется случайная величина – количество решенных задач для второго студента. Так же исследуется случайная величина 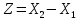 . Построить ряд распределения случайной величины Z, и найти характеристики . Построить ряд распределения случайной величины Z, и найти характеристики 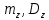 . .Случайная величина 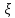 имеет плотность имеет плотность 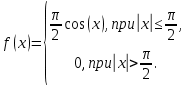 Найти математической ожидание и дисперсию случайной величины 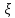 . .Задачу по теории вероятностей одновременно решают 30 студентов. Вероятность того, что за время T задача будет решена, для каждого из студентов равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что абсолютная величина разности между средним числом решивших задачу студентов и математическим ожиданием решивших задачу студентов окажется меньшим 5. Имеется 1500 независимых случайных величин, дисперсия каждой не превосходит 10. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превзойдет 0,5. |