Статистика. Домашнее задание. Вариант 3. Домашнее задание по курсу Статистика
 Скачать 358.5 Kb. Скачать 358.5 Kb.
|
Таблица 4.6.Расчет внутригрупповой дисперсии по пятой группе.
_ х 5 = 125,86 2 5 = 131,92 Таблица 4.7.Расчет внутригрупповой дисперсии по шестой группе.
_ х 6 = 145,70 2 6 = 0,49 Средняя внутригрупповая дисперсия характеризует случайную вариацию результативного признака, возникающих под влиянием других, неучтенных факторов и не зависит от признака-фактора, положенного в основу группировки. Она определяется по формуле: 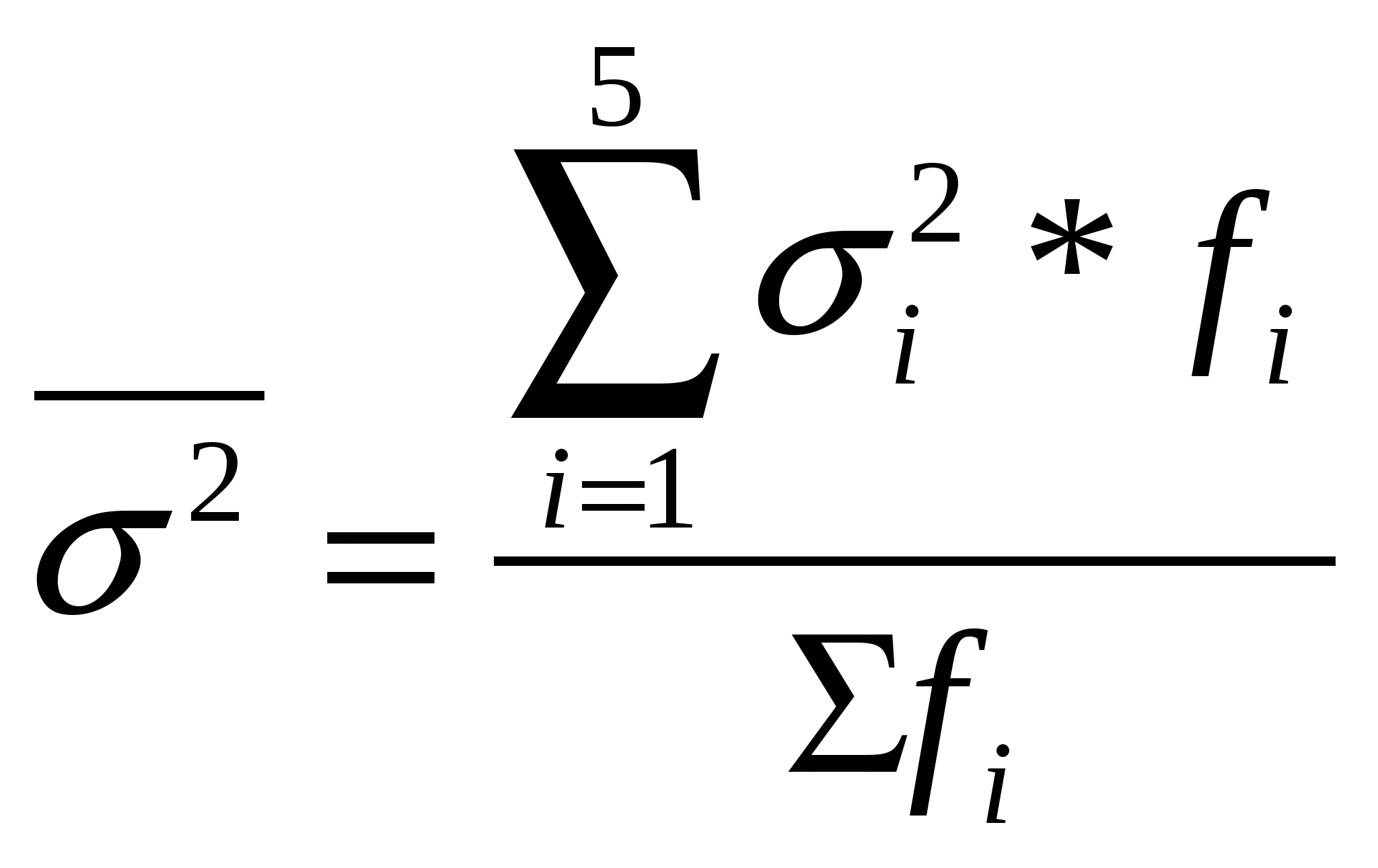 _ 2 = (34,49*7 + 80,75*5 + 25,43*5 + 40,92*4 + 131,92*7+ 0,49*2 ) / 30 =62,01 Межгрупповая дисперсия отражает систематическую вариацию результативного признака, т.е. те различия, которые возникают под влиянием фактора, положенного в основу группировки. Она определяется по формуле: Правило сложения дисперсий: 1215,72 =1153,71+ 62,01 – выполняется Вывод: правило сложения дисперсий выполняется. 5. Анализ зависимости затрат на содержание оборудования от объема выработанной валовой продукции по отчетным данным предприятий за март. Анализ выполняется в следующей последовательности:
5. определяется модель парной зависимости, оценка её достоверности..
Факторный признак (x) - объем выработанной валовой продукции за март. Таблица 5.1. Вспомогательная таблица для расчета σx.
Первичная информация проверяется на однородность по признаку – фактору с помощью коэффициента вариации. _ _ (/ x )* 100%. X = ∑x / n = 86,7 ____________ (x - xср)2 / n =34,87; V x = 40,22% Совокупность неоднородная, так как показатель вариации больше 33%. Проверка первичной информации на нормальность распределения с помощью правила «трех сигм». _ _ _ Интервалы для значения признака - фактора: (x ± σ); (x ± 2σ); (x ± 3σ)., т.е. (86,7–34,87) - (86,7+34,87);(86,7-2*34,87) - (86,7+2*34,87);(86,7-3*34,87) - (86,7+3*34,87). (51,83 – 121,57); (16,96 – 156,44); ( - 17,91 –191,31). Таблица 5.2.
Первичная информация по признаку-фактору не подчиняется закону нормального распределения, однако это не является основанием для отказа от использования корреляционно-регрессионного анализа. 2. Исключение из первичной информации резко выделяющихся единиц, которые по признаку-фактору не попадают в интервал. _ _ x - 3σ ≤ xi ≤ x+ 3σ - 17,91 ≤ xi ≤ 191,31 Резко выделяющихся единиц в первичной информации нет. 3. Для установления факта наличия связи производится аналитическая группировка по признаку-фактору. Группировка выполняется при равных интервалах и числе групп 4. Величина интервала определяется по формуле: i = ( xmax - xmin)/m , где m - число групп. i = (146,4- 33,6)/4 = 28,2 ≈ 29. Таблица 5.3. Вспомогательная таблица для заполнения групповой таблицы.
Таблица 5.4. Зависимость затрат на содержание оборудования от объема выработанной валовой продукции.
Как видно из данных групповой таблицы с увеличением выпуска валовой продукции в марте увеличивается средняя величина затрат на содержание оборудования в марте. 4. Для измерения степени тесноты связи используется линейный коэффициент корреляции: ________________________ _________ r = (Σxy-(Σx·Σy)/n)/ √[Σx² - ((Σx)²/n)][Σy²-(Σy)²/n]; r = (19303,37- 16923,19)/√[ 261960,9- 225489,36][ 1431,4-1270,10]=0,98 Для расчета r использована следующая вспомогательная таблица (табл. 5.5). Таблица 5.5 Вспомогательная таблица для расчета линейного коэффициента корреляции и уравнения связи
Значение линейного коэффициента корреляции (r = 0,98) свидетельствует о наличии прямой и очень тесной связи. Средняя квадратическая ошибка коэффициента корреляции ___ ___ σr = (√1-r²)/(√n-2) =0,04 |r|/σr = 24,5 По таблице 1 определяется t – критерий Стьюдента при Р = 0,95 и к = 30 – 2; tтабл = 2,048 | r | / r > tтабл - критерия (24,5 > 2,048) Следовательно, можно утверждать существенность коэффициента корреляции. Определяется модель связи. График линии средних показывает наличие линейной связи, поэтому используется функция ŷ = a + bx. _ _ _ b = (Σxy-nx·y)/(Σx²-n(x)²) = (19303,37- 30*86,7*6,5)/( 261960,9- 30*7516,89) = 2396,87/36454,2 = 0,06 _ _ (x = (2600,9/30) = 86,7; y = (195,2/30) = 6,5) _ _ a = y - bx = 6,5 - 5,202 = 1,3 Модель связи следующая: ŷ = 1,3 + 0,06x Для возможности использования линейной функции определяется величина ω² = (η²-r²)/(m-2)÷(1-η²)/(n-m), которая сравнивается с F-критерием. _____ _ _ Для расчета ω² исчисляется корреляционное отношение η = √δ²/σ²y; δ² = ∑((yi-yo)²∙ni)/∑ni. Для расчета используются данные таблицы 5.4. δ² =((3,36 - 6,5)²∙7 + (5,12 - 6,5)²∙5 + (6,72 - 6,5)²∙5 + (7,40 - 6,5)²∙4+ (8,91 - 6,5)²∙7+ (10,25 - 6,5)²∙2) / 30 = 5,03 σ²y = ∑d²y /n=∑(y-y)²/n = ((2,6-6,5)²+(6,8-6,5)²+(7,8-6,5)²+(10,9-6,5)²+(3,1-6,5)²+(5,9-6,5)²+(6,8-6,5)²+(9,2-6,5)²+(4,6-6,5)²+(7,4-6,5)²+(4,5-6,5)²+(10,1-6,5)²+(4,2-6,5)²+(8,4-6,5)²+(2,6-6,5)²+(3,3-6,5)²+(6,3-6,5)²+(9,6-6,5)²+(7,4-6,5)²+(7,6-6,5)²+(3,5-6,5)²+(7,2-6,5)²+(8,7-6,5)²+(6,1-6,5)²+(8,3-6,5)²+(9,1-6,5)²+(8,6-6,5)²+(5,8-6,5)²+(4,2-6,5)²+(4,6-6,5)²)/30 = 188,7/30 = 6,3 _____ η = √5,03/6,3 =0,89 Следовательно, корреляционное отношение показывает наличие очень тесной связи. ω² = -(0,08415/0,007425) = - 11,3 При вероятности P = 0,95 (α = 0,05) k1= m -2 = 2 и k2=n-m=26; Fтабл=3,37 2. Так как ω² меньше Fтабл, то возможность использования линейной функции не опровергается. Средняя квадратическая ошибка уравнения _________ ______ Se = √∑(y-ŷ)²/n-l =√ 7,015/28 = 0,25 _ (Se/y)*100 = 3,8%. Полученное отношение значительно меньше 15%, поэтому уравнение достаточно хорошо отображает взаимосвязь двух признаков и может быть использовано в практической работе. 6. Предприятия, по которым приведены отчетные данные, представляют собой двадцати процентную выборку из числа предприятий данной отрасли в регионе. Требуется определить: а) среднюю стоимость основных фондов предприятия отрасли в регионе, гарантируя результат с вероятностью 0,997; б) вероятность того, что среднее значение стоимости основных фондов отличается от полученной по выборке величине не более, чем на 1,5 млн. руб. Расчет всех необходимых показателей по выборочным данным произвести на основе группировки предприятий по стоимости основных фондов, приняв равные интервалы группировки при числе групп 5.
Таблица 6.1
а) Доверительный интервал для генеральной средней с вероятностью Р определяются по формуле: _ _ х - х x х + y х – средний уровень признака по выборке: x = ∑x'f/∑f = 620,2/30 = 21 S² = ∑(x'-x)²·f /∑f = 1202,44/30 = 40,08 Величина xназывается предельной ошибкой выборки и определяется по формуле: xt*x где x- величина средней квадратической стандартной ошибки t - коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки. При вероятности 0, 997 t = 2,98 3. ___________ _______________ μx = √(S²/n)*(1-n/N) = √(1606,4064/30)*(1-0,2) =6,54 x 6,54*2,98 = 19,5. Доверительные интервалы для генеральной средней с вероятностью Р = 0,997: _ 21 – 19,5≤ x ≤ 21 + 19,5 б) Для решения 2-ого задания известна допустимая ошибка ∆x = 1,5. tф = ∆x/μx = 1,5/ 6,64 = 0,22 μx = 6,64 (из п. 1) По таблице на основе значения t определяется вероятность того, что ошибка не превысит заданной величины 4. При t = 0,22 вероятность Р = 0,1741. Список используемой литературы:
Сноски: 1 Приложение 6 2 Приложение 5 3 Приложение 3 4 Приложение 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
