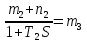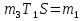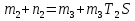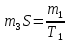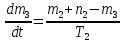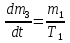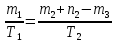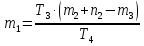Допускаю к защите Руководитель Д. А. Панасецкий Анализ устойчивости электроэнергетических систем пояснительная записка к курсовой работе по дисциплине Электромеханические переходные процессы 021. 00. 00 Пз
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Министерство образования и науки Российской Федерации ФГБОУ ВО «ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» ИНСТИТУТ ЭНЕРГЕТИКИ Кафедра электрических станций, сетей и систем Допускаю к защите Руководитель______________ /Д.А. Панасецкий/ Анализ устойчивости электроэнергетических систем ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине: «Электромеханические переходные процессы» 1.021.00.00 ПЗ Выполнил студент группы ЭСб-13-1 ________ ??? Нормоконтроль ________ Д.А. Панасецкий Курсовая работа защищена с оценкой _______________ Иркутск 2016 Министерство образования и науки Российской Федерации ФГБОУ ВО «Иркутский НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ технический университет» ИНСТИТУТ ЭНЕРГЕТИКИ Кафедра электрических станций, сетей и систем ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ по дисциплине «Электромеханические переходные процессы» студенту __________________???____________________гр. ЭСб -_______???______ (фамилия, инициалы) (шифр группы) Тема работы: Анализ устойчивости электроэнергетических систем СОДЕРЖАНИЕ РАБОТЫ Задача №1. Составить уравнения динамической системы с использованием метода пространства состояний, которые соответствуют нижеприведенной структурной схеме.  Задача №2. Используя метод деления пополам, рассчитать предельное время ликвидации короткого замыкания на шинах бесконечной мощности в системе без диссипации и в системе с диссипацией. Для предельного времени ликвидации короткого замыкания с учетом и без учета диссипации рассчитать площадки ускорения и торможения. Для рассчитанных предельных ситуаций построить угловые характеристики, обозначив на них площадки ускорения и торможения. В системе с диссипацией рассчитать асинхронный ход генератора. Проанализировать полученные результаты. Сделать выводы по всем пунктам. Уравнения системы станция – шины бесконечной мощности (ШБМ)  Схема системы станция – шины бесконечной мощности (ШБМ): 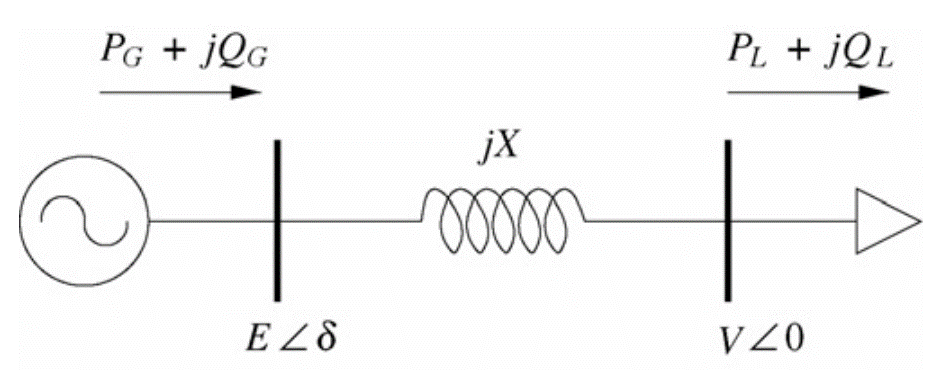 Задача №3. Используя метод деления пополам, рассчитать режим, предельный по статической апериодической устойчивости для системы станция – узел нагрузки. Проанализировать динамику движения собственных чисел динамической системы при утяжелении. Проанализировать динамику изменения напряжения на шинах узла нагрузки и угла по передаче при утяжелении режима. Рассчитать динамику движения переменных состояния при нарушении статической апериодической устойчивости системы станция – узел нагрузки. Проанализировать полученные результаты. Сделать выводы по всем пунктам. Уравнения системы станция – узел нагрузки 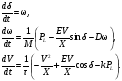 Схема системы станция – узел нагрузки:  Литература
Курсовая работа выполняется в соответствии с Вариантами, приведенными ниже: Задача №1. Вариант №???
Задача №2. Вариант №???
Задача №3. Вариант №???
Дата выдачи задания “___20___” ___сентября_______________2016 г. Преподаватель: ___________ /Панасецкий Д.А./ «__20__»_____ сентября ____2016 г. ОглавлениеВВЕДЕНИЕ 7 Задача №1. Составление уравнений динамической системы с использованием метода пространства состояний. 8 Выводы к Задаче №1 10 Задача №2. Расчет предельного времени ликвидации короткого замыкания на шинах бесконечной мощности в системе без диссипации и с диссипацией. Анализ и построение угловых характеристик. Асинхронный ход в системе. 10 2.1 Расчет предельного времени ликвидации КЗ на ШБМ в системе без диссипации (D0=0). 10 2.2 Расчет предельного времени ликвидации КЗ на ШБМ в системе С ДИССИПАЦИЕЙ (D0 не равно нулю). 13 2.3. Расчет асинхронного хода в системе с диссипацией (D0 не равно нулю). 15 Выводы к Задаче №2 16 Задача №3. Расчет режима, предельного по статической апериодической устойчивости для системы станция – узел нагрузки. Анализ динамики движения собственных чисел. Расчет динамики при нарушении статической апериодической устойчивости узла нагрузки. 16 3.1. Расчет режима, предельного по статической апериодической устойчивости. 17 3.2. Расчет динамики при нарушении статической апериодической устойчивости. 20 Выводы к Задаче №3 21 ЗАКЛЮЧЕНИЕ 22 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 23 ВВЕДЕНИЕВажнейшее значение в проблеме переходных электромеханических процессов в электрических системах придается вопросам устойчивости. Аварии, связанные с нарушением устойчивости параллельной работы в крупных электрических системах, влекут за собой нарушение электроснабжения больших энергорайонов. Ликвидация таких аварий и восстановление нормальных условий работы электрических систем представляют большие трудности. Подобные тяжелые последствия заставляют уделять значительное внимание вопросам устойчивости. В проблеме устойчивости различают статическую и динамическую устойчивость. Под статической устойчивостью понимают способность системы самостоятельно восстановить исходный режим работы при малом возмущении. Статическая устойчивость является необходимым условием существования установившегося режима работы системы, но отнюдь не гарантирует способности системы продолжать работу при резких нарушениях режима, например, при коротких замыканиях. Эта сторона проблемы, так называемая динамическая устойчивость системы, также отражена в курсовой работе. Полезно дописать что-нибудь свое, либо вообще написать свой текст во введении! Задача №1. Составление уравнений динамической системы с использованием метода пространства состояний.Исходные данные для расчета: 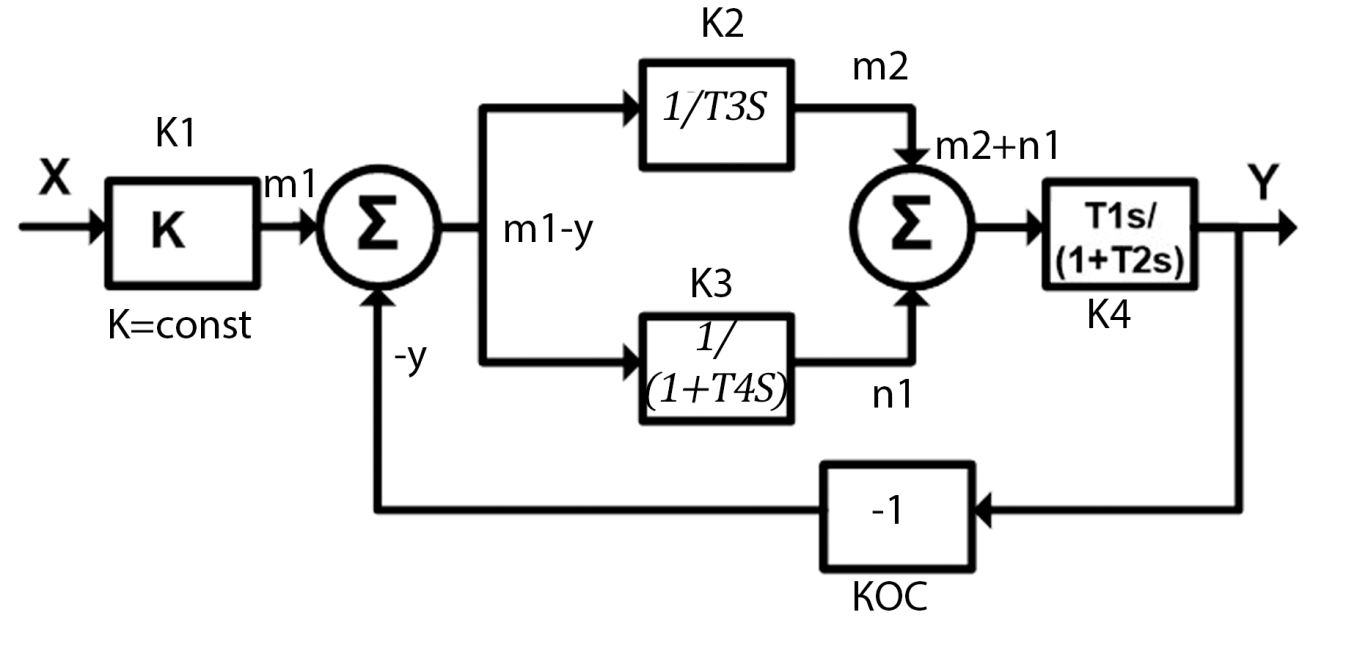 Рисунок 1-структурная схема К1 – пропорциональное звено К2 – интегральное звено К3 – апериодическое звено К4 – дифференциальное звено КОС (коэф-т обратной связи) = -1 Необходимо составить уравнения метода пространства состояний, которые соответствуют нижеприведенной структурной схеме. Решение: 1) 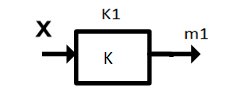 m1=Kx 2) 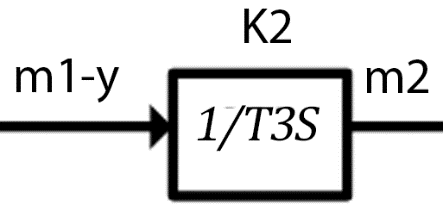 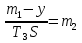 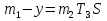 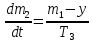 3) 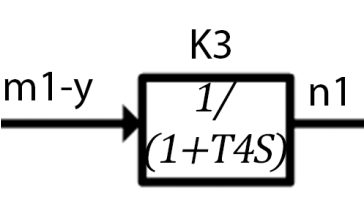 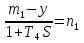 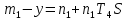 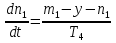 4) 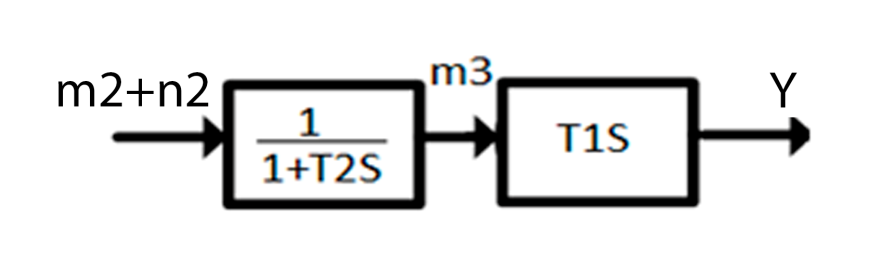
Выводы к Задаче №1Каждый пишет свое, что и как понял, чему его научила данная задача, чтобы не под копирку у всех было! Задача №2. Расчет предельного времени ликвидации короткого замыкания на шинах бесконечной мощности в системе без диссипации и с диссипацией. Анализ и построение угловых характеристик. Асинхронный ход в системе. Исходные данные для расчета:
2.1 Расчет предельного времени ликвидации КЗ на ШБМ в системе без диссипации (D0=0).Цель. Расчет предельного времени ликвидации КЗ на ШБМ в системе без диссипации (D0=0). Задача. Используя метод деления пополам, рассчитать предельное время ликвидации КЗ на ШБМ. Проанализировать полученные результаты. Метод деления пополам для поиска предельного времени ликвидации КЗ:
Расчет площадок ускорения и торможения: Площадка ускорения: Susk=Pm0*(delta2-delta1)+E0*Vdist/X0* (cos(delta2)-cos(delta1)) Площадка торможения: Storm=E0*V0/X0*(cos(delta2)-cos(delta3))-Pm0*(delta3-delta2) Результаты расчета предельного времени ликвидации КЗ для системы без диссипации:
Результаты расчета для системы без диссипации:
Результаты расчета. Угловые характеристики. Площадки ускорения и торможения без учета диссипации: 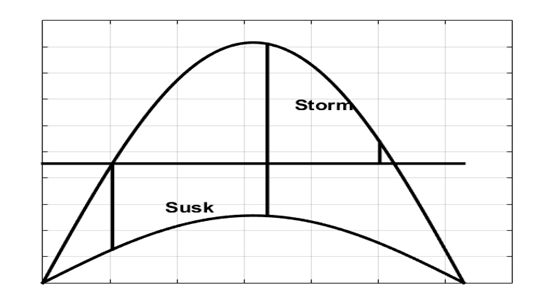 Результаты расчета. Динамика переменных состояния. 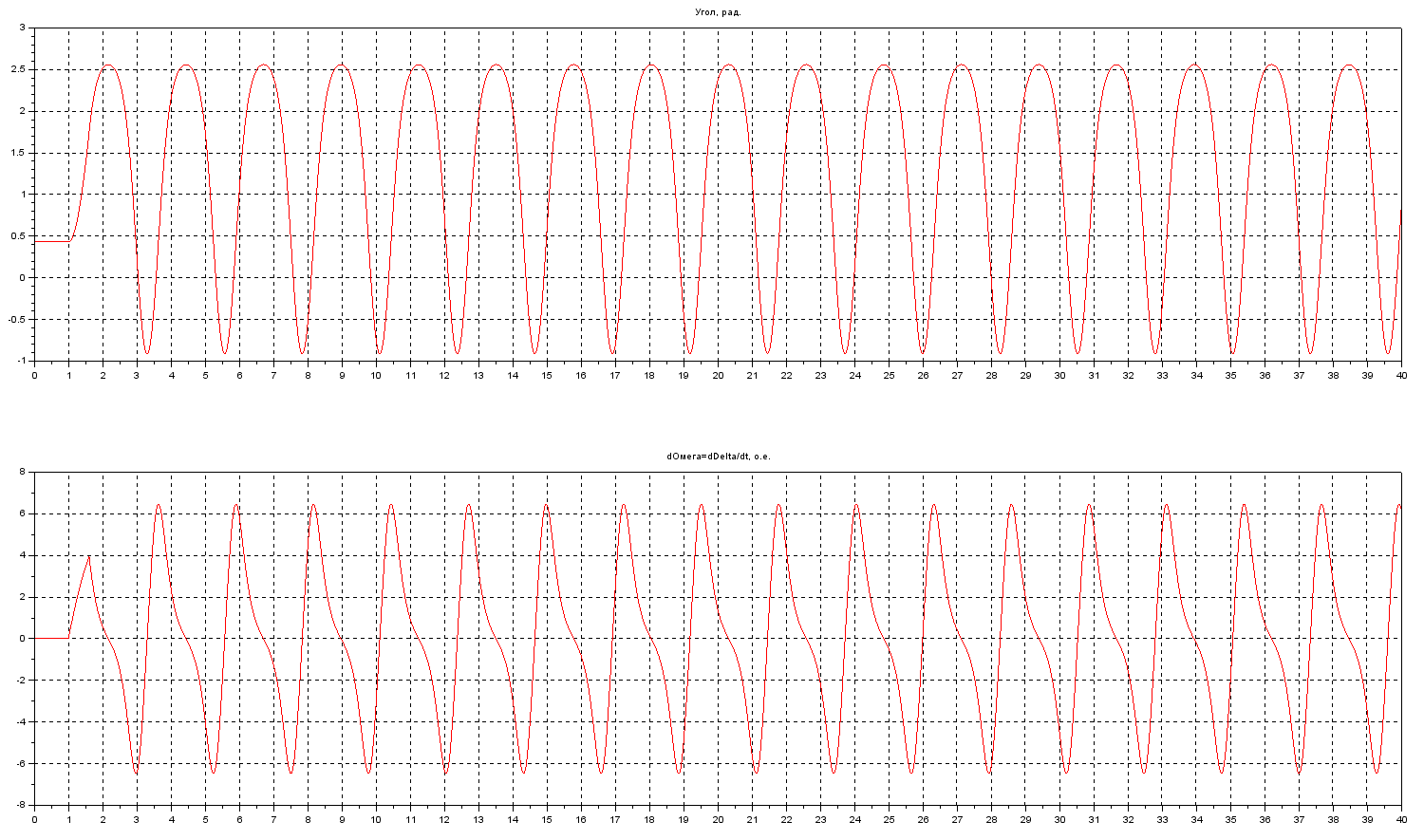 2.2 Расчет предельного времени ликвидации КЗ на ШБМ в системе С ДИССИПАЦИЕЙ (D0 не равно нулю).Цель. Расчет предельного времени ликвидации КЗ на ШБМ в системе С ДИССИПАЦИЕЙ (D0 не равно нулю). Задача. Используя метод деления пополам, рассчитать предельное время ликвидации КЗ на ШБМ. Проанализировать полученные результаты. Метод деления пополам для поиска предельного времени ликвидации КЗ:
Расчет площадок ускорения и торможения: Площадка ускорения: Susk=Pm0*(delta2-delta1)+E0*Vdist/X0* (cos(delta2)-cos(delta1)) Площадка торможения: Storm=E0*V0/X0*(cos(delta2)-cos(delta3))-Pm0*(delta3-delta2) Результаты расчета предельного времени ликвидации КЗ для системы с диссипацией:
Результаты расчета для системы с диссипацией:
Результаты расчета. Угловые характеристики. Площадки ускорения и торможения с учетом диссипации: 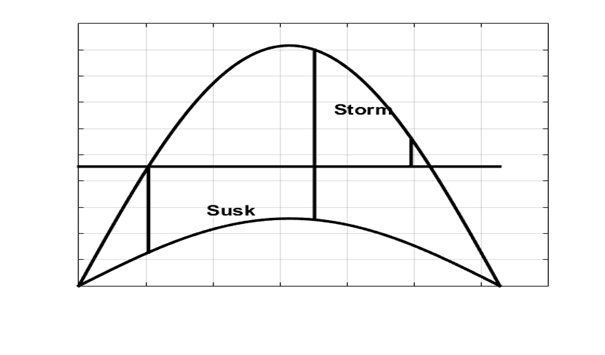 Результаты расчета. Динамика переменных состояния с учетом диссипации. 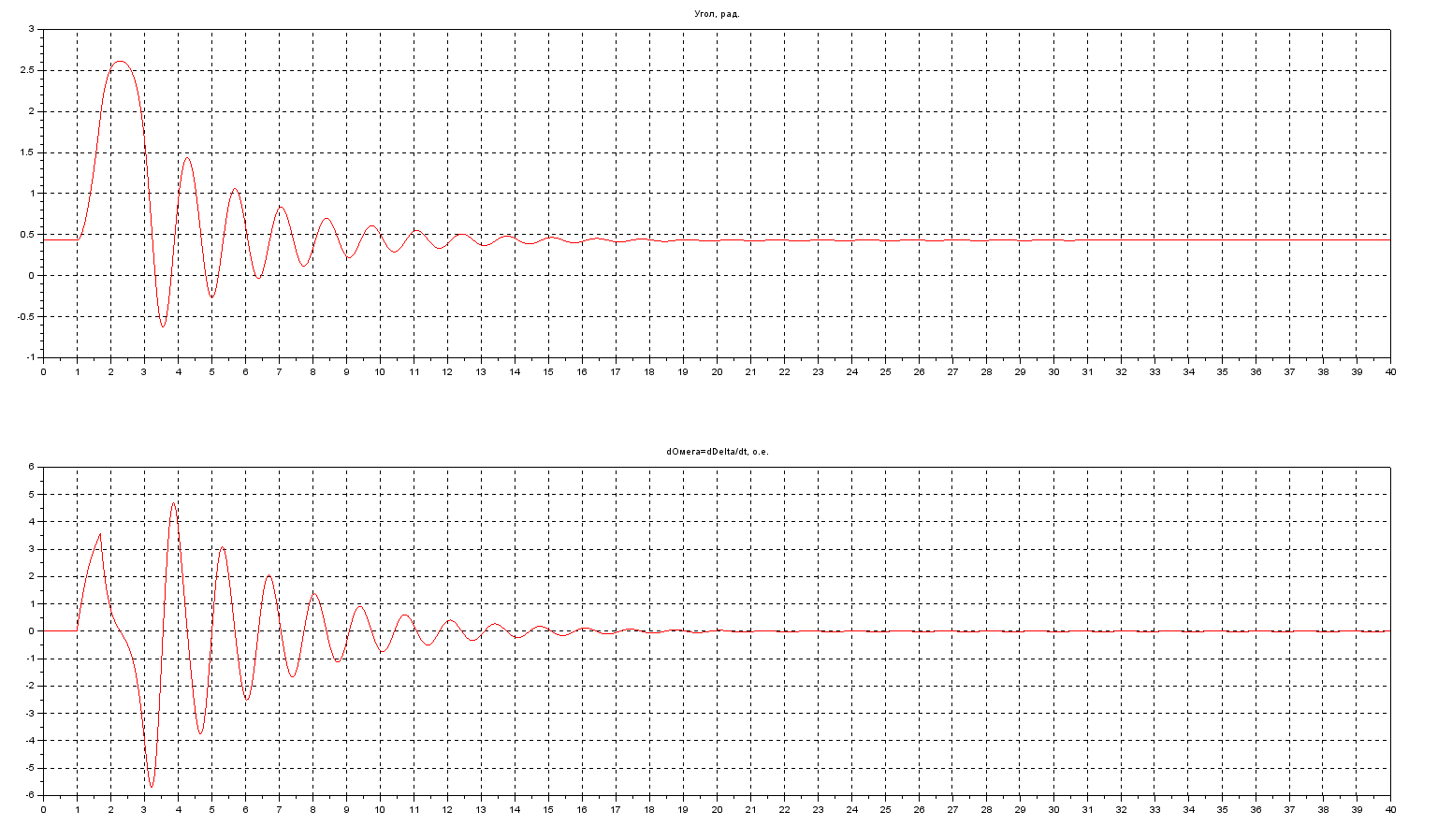 Результаты расчета. Динамика переменных состояния с учетом и без учета диссипации.  2.3. Расчет асинхронного хода в системе с диссипацией (D0 не равно нулю).Цель. Расчет асинхронного хода в системе с диссипацией (D0 не равно нулю). Задача. Ускоряя генератор (omega), рассчитать асинхронный ход. Проанализировать полученные результаты. Результаты расчета. Динамика переменных состояния при асинхронном ходе с учетом диссипации. Omega0=8 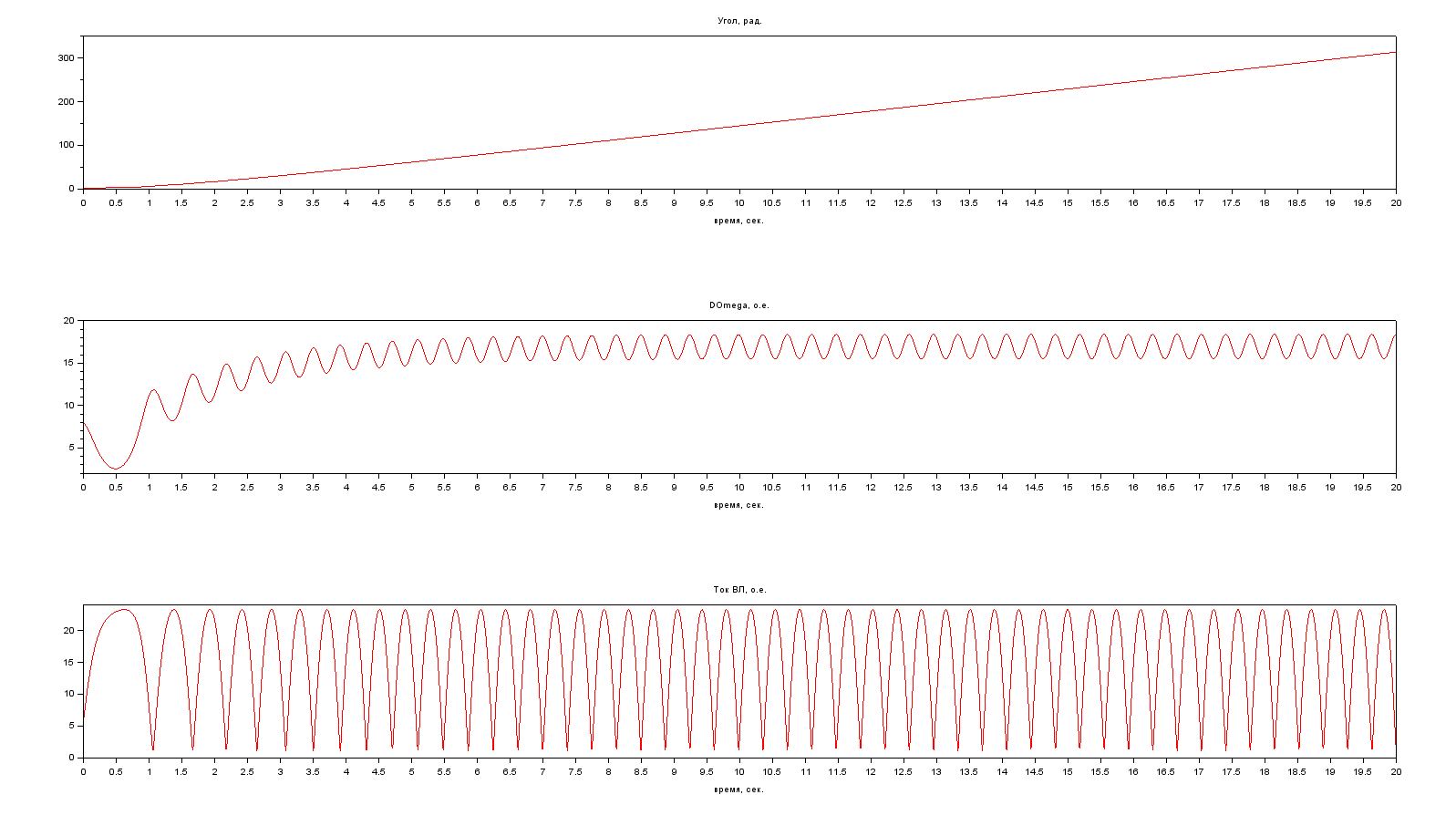 Выводы к Задаче №2Каждый пишет свое, что и как понял, чему его научила данная задача, чтобы не под копирку у всех было! Задача №3. Расчет режима, предельного по статической апериодической устойчивости для системы станция – узел нагрузки. Анализ динамики движения собственных чисел. Расчет динамики при нарушении статической апериодической устойчивости узла нагрузки. Исходные данные для расчета:
3.1. Расчет режима, предельного по статической апериодической устойчивости.Цель. Расчет режима, предельного по статической апериодической устойчивости. Задача. Используя метод деления пополам, рассчитать режим, предельный по статической апериодической устойчивости. Проанализировать полученные результаты. Для рассматриваемой системы станция – узел нагрузки предельная ситуация существования установившегося режима соответствует режиму, предельному по статической апериодической устойчивости. Таким образом, задача сводится к поиску предельного установившегося режима. Метод деления пополам для поиска предельного установившегося режима:
Результаты расчета режима, предельного по статической апериодической устойчивости:
Результаты расчета. Динамика движения собственных чисел при утяжелении. Eig3 Результаты расчета. Динамика изменения напряжения при утяжелении. U=f(P) Результаты расчета. Динамика изменения угла при утяжелении. delta=f(P) 3.2. Расчет динамики при нарушении статической апериодической устойчивости.Цель. Расчет динамики при нарушении статической апериодической устойчивости узла нагрузки. Задача. Утяжелить предельный режим в динамике. Получить апериодическую неустойчивость. Проанализировать полученные результаты. Построить динамику изменения переменных состояния. Последовательность действий: 1. Начинаем расчет динамики с рассчитанного предельного установившегося режима. 2. В момент времени t>1 незначительно увеличиваем мощность узла нагрузки. 3. Увеличение нагрузки должно привести к возникновению статической апериодической неустойчивости. Примечание: Система не может нормально функционировать после нарушения устойчивости, так как не обеспечивается нагрузка узла. При слишком длительном времени моделирования будет возникать сингулярность – отсутствие решения в динамике. Результаты расчета переменных состояния. 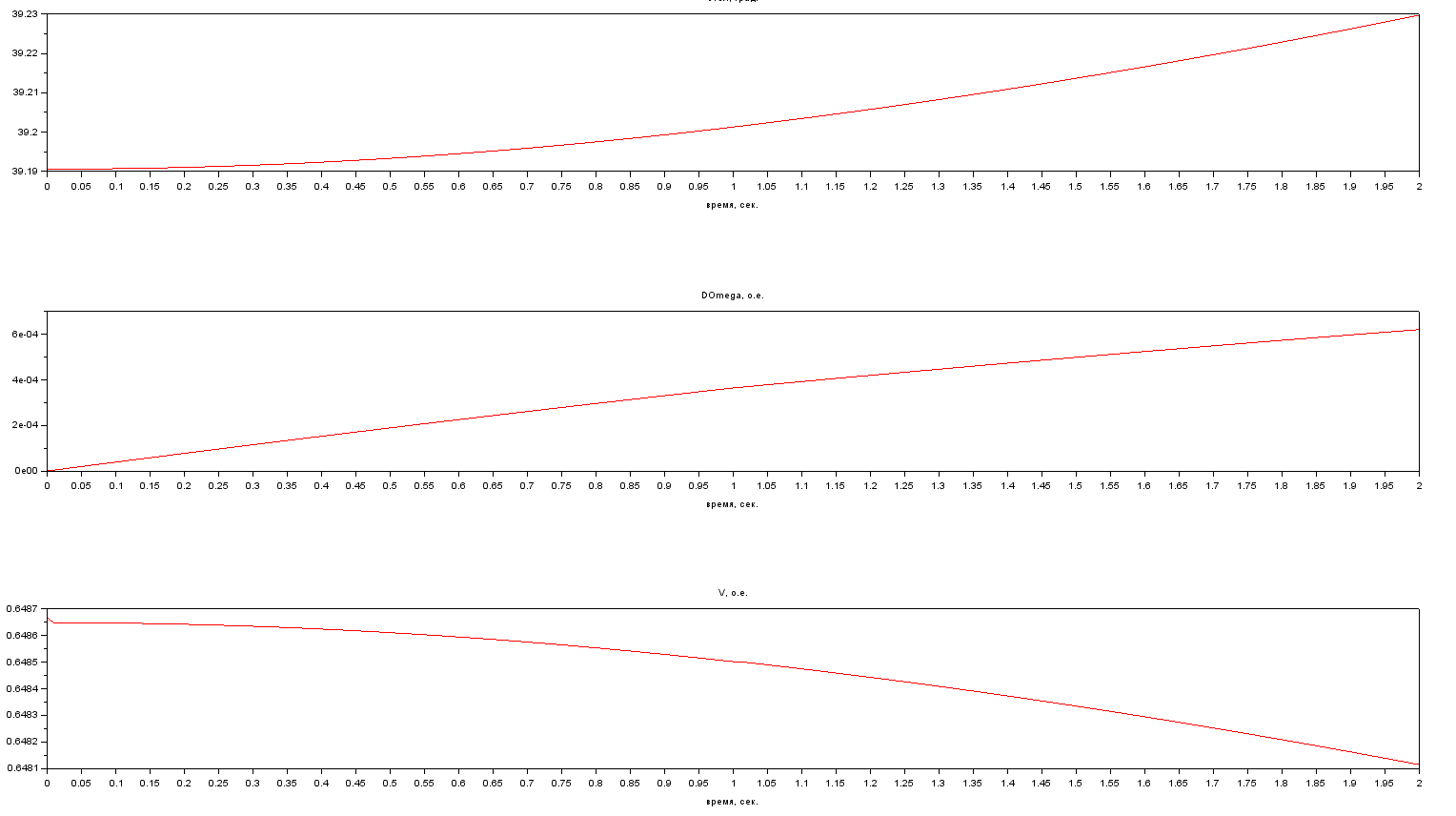 Выводы к Задаче №3Каждый пишет свое, что и как понял, чему его научила данная задача, чтобы не под копирку у всех было! ЗАКЛЮЧЕНИЕНапишите, чему научились, какой фан получили от всего увиденного и просчитанного! СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||