контрольная электронные приборы бгуир. Двоичные слова с выхода ацп преобразуются в канальные сигналы
 Скачать 383.1 Kb. Скачать 383.1 Kb.
|
|
Задание 2. Двоичные слова с выхода АЦП преобразуются в канальные сигналы. Носитель 1-ой ступени модуляции – Д-последовательность. Носитель 2-ой ступени модуляции – гармонический сигнал, известный точно. Модуляция носителя – по форме. Период последовательности –16. Длина блока – 4. Символы кода последовательности: -1, 1. Определить: 1. Математическое выражение канального сигнала. 2. Структурную схему формирователя канального сигнала, включающую: для вариантов с М-последовательностью – генератор синхроимпульсов, генератор шумоподобного сигнала, устройство для получения циклических сдвигов, АЦП, модуляторы 1-й и 2-й ступеней; В вариантах с М-последовательностью и модуляцией ШС по форме привести структурную схему генератора последовательности и структурную схему устройства для получения необходимого числа циклических сдвигов этой М-последовательности. 3. Привести описание работы формирователя канального сигнала и временные, спектральные диаграммы, поясняющие его работу. В описании дайте характеристику синхросигналов (на какой блок поступают и какую функцию выполняют). Приведите основные параметры: длительность и период повторения. Дайте краткую характеристику работы генераторов шумоподобных сигналов и модуляторов 1-й и 2-й ступени, увязывая её с построенными временными и спектральными диаграммами. Рассчитать: энергию, мощность, ширину спектра модулирующего сигнала; энергию, мощность, автокорреляционную функцию сигнала на выходе 1-ой ступени модуляции, длину этого сигнала и его базу. Для множества радиоимпульсов дискретного ЧМ сигнала и множества кодированных сигналов, из которого формируется ШС, модулированный по форме, найти расстояние между всеми парами этих множеств. Д-последовательность длиной 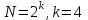 строится из двоичных символов 0,1 и является детерминированным. строится из двоичных символов 0,1 и является детерминированным.Обозначим Д-код длиной 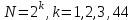 буквой буквой 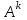 . По этому коду можно найти пару кода . По этому коду можно найти пару кода 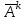 , у которой первые , у которой первые 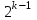 символы совпадают с первыми символы совпадают с первыми 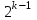 символами кода символами кода 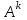 , а последние , а последние 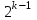 символы не совпадают. По любому коду символы не совпадают. По любому коду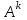 можно найти негативный код можно найти негативный код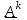 , если у кода , если у кода 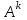 изменить все символы. В семействе Д-кодов имеется изменить все символы. В семействе Д-кодов имеется 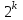 кодовых слов, которые отличаются следующими свойствами. кодовых слов, которые отличаются следующими свойствами.1.Каждому коду семейства соответствует пара, а количество таких пар равно 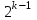 . .2. Д-коды с неравными порядковыми номерами 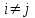 удовлетворяют условию ортогональности. удовлетворяют условию ортогональности.3. Д-коды являются самосинхронизирующимися, т.е. боковые «остатки» их автокорреляционных функций имеют относительно малые значения по сравнению со значениями соответствующих автокорреляционных функций при нулевых сдвигах. 4. Первая половина семейства Д-кодов длиной 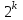 формируется из двух Д-кодов в два раза меньшей длины по правилу: формируется из двух Д-кодов в два раза меньшей длины по правилу: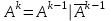 , ,где  - знак присоединения к Д-коду длиной - знак присоединения к Д-коду длиной 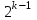 его пары. его пары.Вторая половина семейства формируется из двух Д-кодов в два раза меньшей длины по правилу: 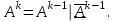 . .Приведём в таблице блоки двоичных чисел, которые выделены из информационного слова источника дискретных сообщений. Например, число разрядов двоичных чисел равно 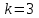 , что соответствует использованию 8ти форм Д-последовательности. , что соответствует использованию 8ти форм Д-последовательности.
Для кодирования различных блоков модуляция по форме предполагает использование отличающихся последовательностей. Исходя из длины блока k=4 определим количество применяемых Д-последовательностей (равно числу блоков) n=2k=16 Так как заранее неизвестно, какой блок поступит с АЦП, то в любой момент времени необходимо иметь возможность сгенерировать (выдать) требуемую последовательность. Такими возможностями обладает генератор, содержащий быстродействующее запоминающее устройство. Выбор той или иной последовательности осуществляется на основании анализа принятого блока. Данное устройство управляет переключателем, который обеспечивает коммутацию последовательности на выход модулятора 1-й ступени. Для передачи информационного кода по каналу связи необходимо промодулировать высокочастотный гармонический сигнал. Эта операция производится с помощью амплитудного модулятора (смесителя). На первый вход смесителя поступает сигнал с выхода модулятора 1-й ступени, на второй вход – высокочастотный монохроматический сигнал с частотой ω0 и известными параметрами (ГСИТ). На рисунке 2.1. приведена формирователя линейного сигнала, где 1 – синхронизатор; Г1…Г16 – генераторы последовательностей; 2 – формирователь блоков и устройство управления ключом; 3 – управляемый переключатель; 4 – генератор ГСИТ; 5 – смеситель. Так как символы последовательности равны -1 или 1, то энергия сигнала в пределах любого единичного интервала не равна нулю. 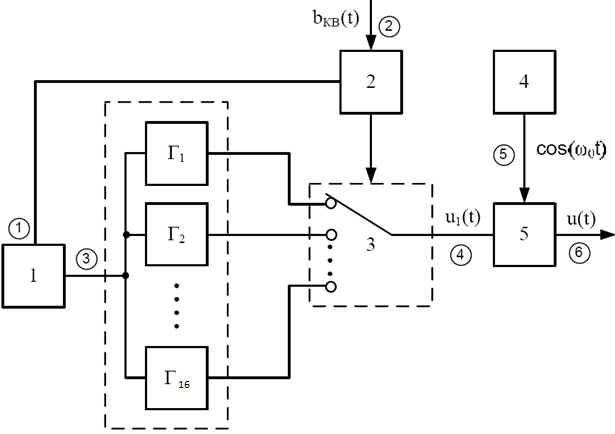 Рис. 2.1. Структурная схема формирователя линейного сигнала Рассчитаем длительность Д-последовательности: 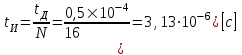 Запишем наш модулирующий сигнал как b(t)=sin(wt)и время 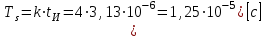 Тогда энергия модулирующего сигнала будет равна 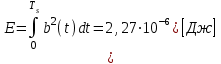 А его мощность равняется: 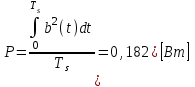 Амплитуда дискретного сигнала на выходе модулятора определяется функцией огибающей импульса в пределах единичного интервала 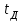 . Энергия сигнала в пределах любого единичного интервала не равна нулю. Такие сигналы называются сигналами с активной паузой. . Энергия сигнала в пределах любого единичного интервала не равна нулю. Такие сигналы называются сигналами с активной паузой.Выберем частоту ГСИТ такой, чтобы в пределах tи умещалось несколько периодов высокой частоты 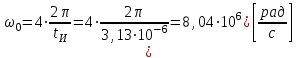 Примем амплитуду для всех сигналов 1 В. Поясним работу схемы на рис. 2.1. временными диаграммами, представленными на рис. 2.2. 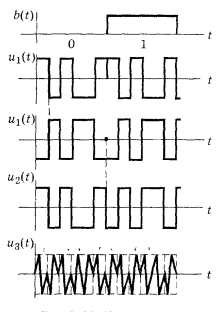 Рис. 2.2. Временные диаграммы работы модулятора Модули спектральной плотности сигнала на выходе АЦП и выходе модулятора 1-ой ступени соответствуют спектру прямоугольного видеоимпульса и описываются выражениями: 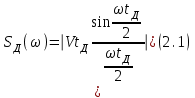 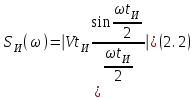 При преобразовании сигнала в модуляторе 2-ой ступени происходит смещение спектра прямоугольного видеоимпульса от частоты 0 на ω0 в сторону положительных и отрицательных частот (спектр раздваивается). При этом максимальное значение уменьшается в 2 раза. 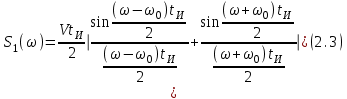 Спектральные диаграммы сигналов представлены на рис. 2.3.  Рис. 2.3. Спектральные диаграммы работы модулятора 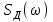 - на выходе АЦП, - на выходе АЦП, 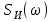 - на выходе модулятора 1-ой ступени, - на выходе модулятора 1-ой ступени, 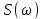 - на выходе модулятора 2-ой ступени. - на выходе модулятора 2-ой ступени.Ширина спектра видеосигнала, состоящего из прямоугольных импульсов, определяется длительностью этих импульсов (учитываем положительные частоты) 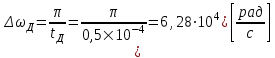 - на выходе АЦП, - на выходе АЦП,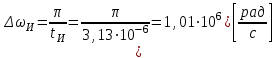 - на выходе модулятора 1-ой ступени. - на выходе модулятора 1-ой ступени.При преобразовании сигнала в модуляторе 2-й ступени его спектральная плотность переносится из области нижних в область высоких частот без искажений спектральных составляющих. Ширина спектра модулированного сигнала при этом увеличивается в два раза 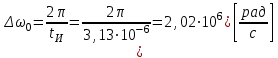 - на выходе модулятора 2-ой ступени. - на выходе модулятора 2-ой ступени.Произведение длительности на ширину спектра называется базой сигнала. N – длина кодового слова. Для данного сигнала база численно равна количеству импульсов в Д-последовательности.  Задание 3. При передаче канального сигнала на этот сигнал накладывается нормальный шум. Мощность шума для всех вариантов равна 0,1 В2. Мощность сигнала на входе приёмника 0,0625 В. 1. Выбрать и изобразить структурную схему оптимального приемника для заданного варианта канального сигнала. Привести описание работы приемника, временные и спектральные диаграммы, поясняющие работу этого приёмника. 2. Вычислить уровни порогов в соответствующих вариантах приемников. 3. Определить вероятность ошибки, которая определяет потенциальную помехоустойчивость оптимального приёмника. 4. Определить и описать математическую модель дискретного канала. привести ненаправленный граф, соответствующий сигналам на его входе и выходе и рассчитанной вероятности ошибки оптимального приёмника. Определить ширину полосы пропускания дискретного канала. Привести название дискретного канала. 5. По исходным данным определить среду распространения и по этой среде определить название канала. Вычислить ширину полосы пропускания этого канала. Под синтезом оптимального приёмника понимают отыскание его структуры. Задача синтеза: найти структуру приёмника, которая удовлетворяет исходным условиям и ограничениям и при этом обеспечивает совокупность показателей качества, наилучших в смысле заданного критерия оптимальности. Математический синтез заключается в математической формулировки совокупности исходных данных и критерия оптимальности, а также в отыскании чисто математическим путем такой структуры приёмника, которая удовлетворяет исходным данным, критерию оптимальности и требуемой совокупностей показателей качества. В качестве критерия оптимальности выберем критерий максимума отношения правдоподобия, записанного в виде неравенства (3.1), причем 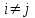 . . 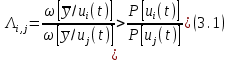 Помеха является нормальным белым шумом со спектральной плотностью N0. Канал связи является дискретно-непрерывным. Время анализа сигнала и шума равно длительности единичного интервала 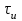 . Используя описание n-мерной плотности распределения вероятности белого шума N(t) и математическое описание непрерывного и дискретно-непрерывного каналов связи, перепишем неравенство (3.1). Все М-последовательности при приёма сигнала известны точно. . Используя описание n-мерной плотности распределения вероятности белого шума N(t) и математическое описание непрерывного и дискретно-непрерывного каналов связи, перепишем неравенство (3.1). Все М-последовательности при приёма сигнала известны точно.Для двоичной системы правило оптимального приёма следует из (3.1) и определяется неравенством (3.2), где 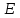 - энергия сигнала, - энергия сигнала, 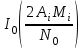 - модифицированная функция Бесселя нулевого порядка. - модифицированная функция Бесселя нулевого порядка.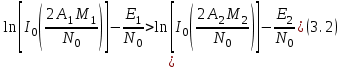 При выполнении неравенства (3.2) на выходе регистрируется 1, в противном случае – 0. Число блоков больше двух, поэтому критерий максимума отношения правдоподобия на основании (3.3) запишем в виде 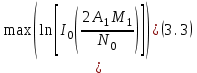 Алгоритм (3.3) довольно просто реализуется с использованием согласованных фильтров. Величину М можно получить, пропуская колебание z(t) через согласованный фильтр и выделяя огибающую на выходе фильтра амплитудным детектором с характеристикой ln I0 (x), где х=2АМ/N0. Структурная схема оптимального приёмника, построенного на согласованных фильтрах, приведена на рис. 3.1.Структурная схема оптимального приемника содержит 16 одинаковых каналов. При приеме одного из 16 ортогональных сигналов на фоне шума только на выходе одного из каналов будет наибольшее среднее напряжение, а на выходах остальных каналов средние значения напряжений будут равны нулю. Так же как и для предыдущих случаев приема, по наибольшему напряжению определяется номер канала и номер сигнала Но номеру сигнала определяется оценка слова блока. 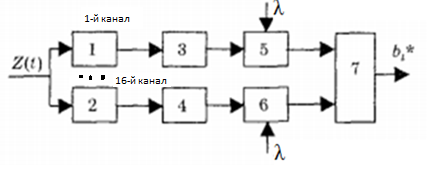 Рис. 3.1. Структурная схема оптимального демодулятора, реализованного на согласованных фильтрах : 1, 2 — согласованные фильтры; 3, 4 — амплитудные детекторы; 5, 6 — сравнивающие устройства; 7 — решающее устройство 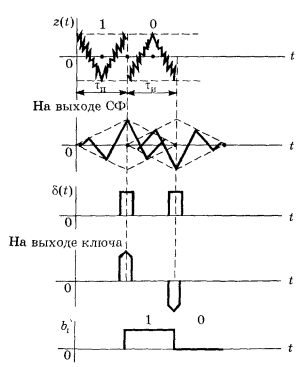 Рис. 3.2. Временные диаграммы, поясняющие работу приёмника Рассчитаем спектральную плотность мощности шума 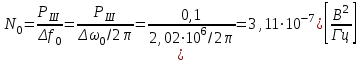 Рассчитаем амплитуду сигнала: 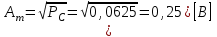 Определим величину энергии последовательности: 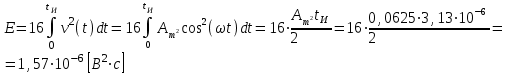 Значение порога, необходимое для работы решающего устройства, определяется из выражений (3.2) и (3.3) и равно: 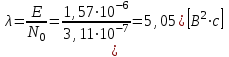 Определим параметр обнаружения h: 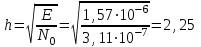 Тогда вероятность ошибки когерентного приёма последовательности определяется по формуле 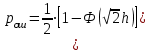 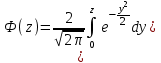 - функция Крампа - функция Крампа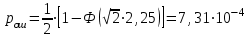 Спектральные диаграммы приведены на рис. 3.3. На первом рисунке изображены спектральные диаграмма полезного сигнала и шума. На втором – спектральная диаграмма выходного сигнала приёмника. 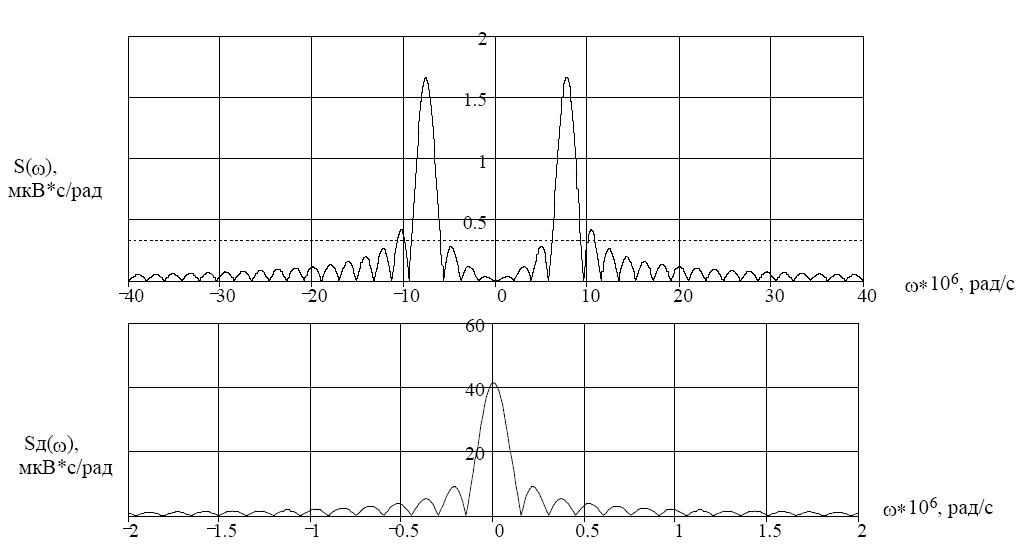 Рис. 3.3. Спектральные диаграммы, поясняющие работу приёмника Рассмотрим математическую модель m-ичного канала связи. Математическая модель канала связи, необходимая для проведения исследований, считается заданной, если известны оператор преобразования, а также условия и ограничения, накладываемые как на канал, так и на входные и выходные сигналы. Математическая модель реального канала связи является достаточно сложной. Это объясняется следующими причинами: Оператор L, кроме линейных, содержит также нелинейные и параметрические преобразования. В канале присутствуют помехи. Входной сигнал может быть случайным. Часто сложная математическая модель не позволяет найти решение поставленной задачи. Поэтому пользуются упрощенными моделями. В них используют представление канала в виде последовательно соединенных четырехполюсников. Полезным является также выделение из канала его дискретной, непрерывной и дискретно непрерывных частей. Для дискретного m-ичного канала связи сигналы на его входе и выходе являются дискретными. Математическая модель этого канала определяется: а) алфавитом кодовых символов на входе 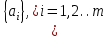 и на выходе и на выходе 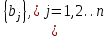 ; ;б) априорными вероятностями появления символов на входе канала; в) вероятностями перехода Р(bj/ai), которые определяют вероятность того, что при передаче символа ai на выходе канала появится символ bj. Если интересоваться скоростью передачи информации по каналу, то следует также задать число символов, подаваемых в среднем в единицу времени на вход канала. Однако эта характеристика рассматриваться не будет. Совместная вероятность подачи символа ai на вход и появление символа bj на выходе: 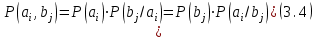 Вероятность того, что на вход подан символ ai при условии, что на выходе появится символ bj (апостериорная вероятность): 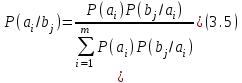 Дискретный канал называется однородным (стационарным) и без памяти, если вероятности переходов 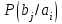 для каждой пары i, j не меняются во времени и не зависят от того, какие символы передавались ранее. для каждой пары i, j не меняются во времени и не зависят от того, какие символы передавались ранее.Если эти вероятности зависят от времени, канал называется неоднородным (нестационарным); если же они зависят от символов, переданных ранее, то канал называется каналом с памятью. Если в однородном дискретном канале алфавиты на входе и выходе одинаковы (m=n) и для любой пары i≠jвероятности 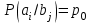 , а для пары i=j , а для пары i=j 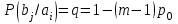 , то такой канал называется симметричным каналом без стирания. , то такой канал называется симметричным каналом без стирания.Если объем алфавита символов на выходе канала n превышает объем алфавита входных символов m, канал называют каналом со стиранием. Для любой модели дискретного канала можно записать, пользуясь сложением в дискретном векторном пространстве (поразрядным, по модулю основания кода m): B[k]=A[k]+E[k], где A[k] и B[k] – случайные последовательности (кодовые комбинации) из k символов на входе и выходе канала; E[k] – случайный вектор ошибки, который в общем случае зависит от A[k]. Различные модели отличаются распределением вероятностей вектора E[k]. При двоичном кодировании (m=2) компоненты (разряды) вектора ошибки принимают значение 0 и 1. Всякая 1 в векторе ошибки означает, что в соответствующем месте передаваемой последовательности символ принят ошибочно, а 0 означает безошибочный прием. Число ненулевых символов в векторе ошибок называется его весом. Он равен расстоянию по Хеммингу d(B[k],A[k]) между переданной и принятой кодовыми последовательностями. Если вероятность Р(bj/ai) не зависит от времени, то такой канал называют однородным. В симметричном однородном канале без памяти алфавит кодовых символов на входе совпадает с алфавитом на выходе, а вероятности перехода определяются равенствами (3.6). 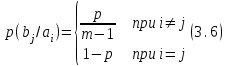 Любой символ ai может перейти в другой символ bj с равной вероятностью p/m-1.Эти переходы определяют вероятность ошибка р. Кроме того, любой символ ai может с вероятностью (1-р) перейти в символ bi, то есть, принят правильно. Для двоичного симметричного канала m=2 и вероятности перехода определяются равенствами (3.7). 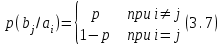 Вероятности перехода (3.9) схематично показаны на рис.(3.4). 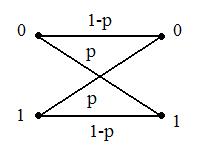 Рис.3.4. Переходные вероятности в двоичном симметричном канале. Вероятность перехода нуля в нуль равна 1-р, а нуля в единицу равна р. Соответственно, вероятность перехода 1 в 1 равна 1-р, а вероятность перехода 1 в нуль равна р. Задание 4. Вычислить производительность источника непрерывных сообщений. Вычислить скорость передачи информации по дискретному каналу. Вычислить пропускную способность дискретного канала. Рассчитать число дискретных каналов, возможных для заданных исходных данных, а также пропускную способность многоканальной системы связи. Вычислить частотную и энергетическую эффективности дискретного канала связи и сравнить эти характеристики с характеристикой идеальной системы связи. Нарисовать структурную схему системы передачи непрерывных сообщений цифровым методом. Привести описание работы системы. Решение:  -энтропия первичного сигнала -энтропия первичного сигнала  определяется формулой 4.1, где определяется формулой 4.1, где 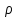 — отношение сигнал/шум. — отношение сигнал/шум.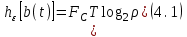 При расчете производительности источника непрерывных сообщений мощность помехи на выходе системы рекомендуется вычислять для заданной линейной шкалы квантования по формуле: 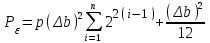 , ,где Р – вероятность ошибки при передаче двоичной информации по каналу связи, 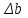 – интервал квантования, n – число разрядов двоичных кодовых слов на выходе АЦП. – интервал квантования, n – число разрядов двоичных кодовых слов на выходе АЦП.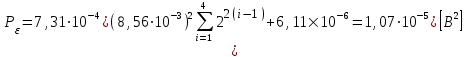 Производительность источника непрерывных сообщений определяется формулой 4.2: 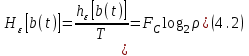 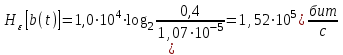 Для процессов, ограниченных по спектру и мощности, пропускная способность определяется формулой Шеннона (4.3), 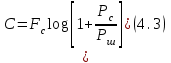 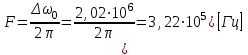 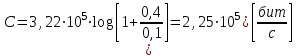 Из формулы видно, что пропускная способность непрерывного канала связи растет с ростом ширины полосы канала F и отношением сигнал/шум. Значит, заданная пропускная способность может быть достигнута либо изменением ширины полосы, либо изменением отношения сигнал/шум. Система связи является многоканальной, если она обеспечивает передачу нескольких сообщений по одной общей линии связи. Многоканальная передача сообщений позволяет приблизить скорость передачи информации к пропускной способности линии связи, которая намного больше производительности источника сообщений. Очевидно, что суммарная производительность нескольких независимых источников должна быть меньше пропускной способности линии С. 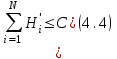 Ширина полосы линии связи равна F0=66 МГц. Максимальное количество каналов, организуемых при использовании данной линии связи равно: 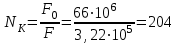 Под эффективностью понимают некоторую функцию показателей качества, которая характеризует систему связи с технической точки зрения. Энергетическая эффективность определяет эффективность использования энергии сигнала. 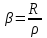 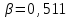 Частотная эффективность – эффективность использования полосы канала: 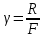 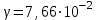 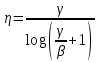 – коэффициент пропускной способности. – коэффициент пропускной способности.В идеальной системе связи 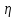 сколь угодно близка к единице при сколь угодно малой вероятности ошибки. Частотная эффективность изменяется в пределах от 0 до ∞, а энергетическая эффективность от - ∞ до 1/ln2. сколь угодно близка к единице при сколь угодно малой вероятности ошибки. Частотная эффективность изменяется в пределах от 0 до ∞, а энергетическая эффективность от - ∞ до 1/ln2.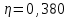 Максимальное значение энергетической эффективности: 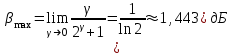 Цифровые методы передачи обладают, по сравнению с аналоговыми (непрерывными) методами передачи, более высокой помехоустойчивостью. Обычно цифровые методы передачи непрерывных сообщений включают в себя методы формирования и обработки сигналов на основе их отображения совокупностью чисел, а также методы передачи этой совокупности по каналу связи.Для согласования непрерывного источника сообщений с дискретным каналом связи на передающей стороне введен аналого-цифровой преобразователь сигнала, а для согласования дискретного канала связи с получателем непрерывного сообщения на приемной стороне введен цифро-аналоговый преобразователь (ЦАП). Преобразование непрерывного сообщения с помощью АЦП в двоичный код называется импульсно-кодовой модуляцией (ИКМ). Сигнал ИКМ поступает на передатчик. В зависимости от вида линии связи сигнал ИКМ соответствующим образом преобразуется. В приемнике двоичные кодовые комбинации после демодуляции и регенерации поступают на ЦАП, где преобразуются вначале в квантованные отсчеты, которые затем пропускаются через фильтр нижних частот для получения непрерывного сообщения. 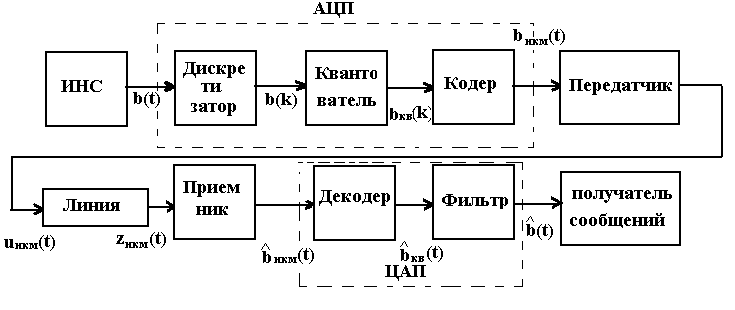 Рис. 4.1. Структурная схема системы цифровой передачи непрерывных сообщений 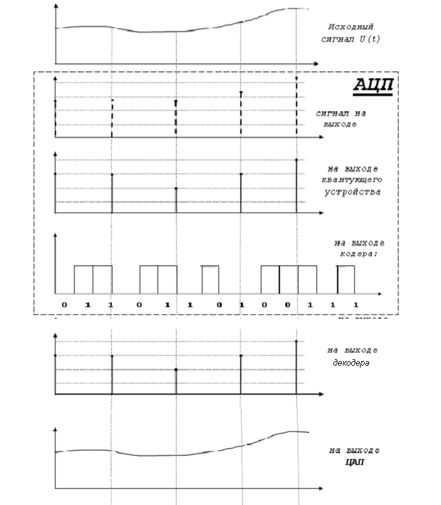 Рис. 4.2.Временые диаграммы, поясняющие работу цифровой системы связи Литература 1.Клюев Л.Л. Теория электрической связи.- Мн.: Дизайн ПРО,1998, 336с. 2.Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М., Теория передачи сигналов.-М.: Радио и связь,1986,304с. 3.Баскаков С.И. Радиотехнические цепи и сигналы.-М.: Высшая школа,1988,448с. 4. Кловский Д.Д., ШилкинВ.А. Теория электрической связи.- М.: Радио и связь,1990,208с. 5.Заездный А.М. Основы расчетов по статистической радиотехнике. М.: Связь,1969,447с. 6. Алексеев А.И., Шереметьев А.Г., Тузов Г.И., Глазов Б. И. Теория и применение псевдослучайных сигналов. – М.: Наука,1969. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
