Раздел
|
|
ФИО педагога
|
|
Дата
|
|
Класс
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Двоичное представление информации
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
5.2.1.4 – пояснять, что вся информация для компьютера представляется в двоичном виде
|
Цель урока
|
Пояснять, как информация представляется в компьютере
Узнают историю систем счисления
Познакомить с основными понятиями систем счисления
Познакомить с десятичной системой счисления
Познакомить с двоичной системой счисления
Познакомить с Римской системой счисления
Научить переводить числа из десятичной в двоичную системы счисления
|
Критерии успеха
|
Знают, как информация представляется в компьютере
|
Ход урока
|
Этапы урока
|
Деятельность учителя
|
Деятельность обучающихся
|
Оценивание
|
Ресурсы
|
Организационный момен
|
Психологический настрой. Деление на группы.
Каждый учащийся получает номер от 1 до 4. Учащиеся формируют группы по полученным номерам
С помощью рисунков ,определите тему нашего урока
Тема урока: Двоичное кодирование числовой информации в памяти компьютера
Запишем тему в тетрадь.

|
Настраиваются на положительный настрой урока.
|
|
видеоролик
|
Изучение нового материала
|
Кодирование –это перевод информации в удобную для передачи обработки или хранения форму с помощью некоторого кода
Декодирование-это процесс восстановления содержания закодированной информации
Вся информация ,которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр – 0 и 1
История возникновения счета
В древние времена, когда люди начали считать, появилась потребность в записи чисел. Количество предметов изображалось нанесением равного количества черточек, зарубок или засечек на какой-либо твердой поверхности.
Позиционные и непозиционные системы счисления
Запишем в тетрадь схему позиционной и непозиционной СС
Римская СС
Позиционные СС
Разберём запись десятичного числа с коэффициентами
Запишем десятичное число в римской СС
Выполним задание
Рассмотрим двоичное представление информации
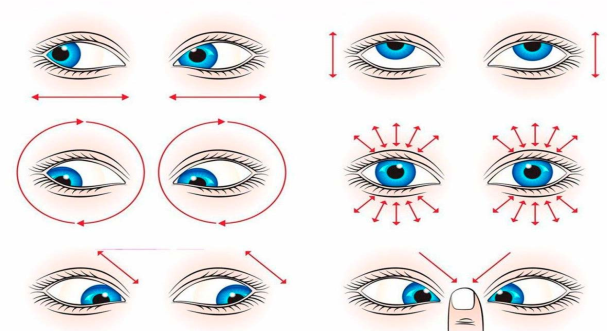
Давайте выполним гимнастику для глаз, следуя схемам и инструкциям.
Система счисления – это способ записи чисел с помощью специальных знаков – цифр.
Система счисления:даёт представления множества чисел; даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);отражает алгебраическую и, арифметическую структуру чисел.Язык чисел, как и любой другой, имеет свой алфавит.
Числа:123, 45678, 1010011, CXL
Цифры:– символы, при помощи которых записывается число.0, 1, 2, … I, V, X, L, …
Разряд- позиция цифры в числе
5 4 321 0 разряд
956784
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Основание системы счисления – это количество цифр, используемых в данной системе счисления.
Базис системы счисления – последовательность степеней основания.
10СС: 10n,10n-1,...,105,104, 103 102,101,100
2CC: 2n,2n-1,...,25,24, 23,22,21,20
8СС: 8n,8n-1,...,85,84, 83 ,82,81,80
16СС: 16n,16n-1,...,165,164, 163,162,161,160
Типы систем счисления:позиционные, непозиционные.
Наиболее распространёнными в ХХI веке являются позиционные системы счисления.
Позиционные – значение цифры зависит от её места (позиции) в записи числа.
Позиционные: шестидесятеричная, двоичная, шестнадцатеричная, десятичная …
В числе 555 первая 5 стоит в позиции сотен, вторая 5 – в позиции десятков, третья5 – в позиции единицы (555=500+50+5).
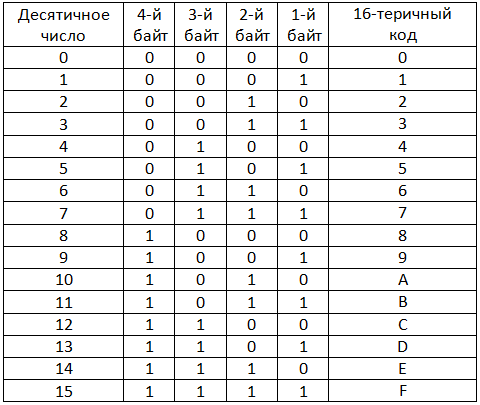
В программировании широкое распространение получили позиционные системы с основанием 8 и 16.В восьмеричной системе счисления применяются 8 цифр-0,1,2,3,4,5,6,7.В шестнадцатеричной системе счисления недостающие цифры заменяют буквами латинского алфавита:А=10,В=11,С=12,D=13,Е=14,F=15.
Непозиционные – значение цифры не зависит от её места (позиции) в записи числа.
Непозиционные: Единичная (унарная) система,римская система, Древнеегипетскаядесятичная система, алфавитная система счисления.
Римская система счисления
I V X L C D M
1 5 10 50 100 500 1000
Алгоритм перевода из 10СС в другие позиционные системы счисления:
Разделить десятичное число на основание системы счисления. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим основания новой системы счисления.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системе счисления.
121
|
2
|
|
|
|
|
|
1
|
60
|
2
|
|
|
|
|
|
0
|
30
|
2
|
|
|
|
|
|
0
|
15
|
2
|
|
|
|
|
|
1
|
7
|
2
|
|
|
|
|
|
1
|
3
|
2
|
|
|
|
|
|
1
|
1
|
12110 = 11110012
57110 = 10738
7467
|
16
|
|
|
|
|
|
11
|
466
|
16
|
|
|
|
|
|
2
|
29
|
16
|
|
|
|
|
|
13
|
1
|
|
|
|
746710 = 1 13 2 1116= 1D2В16
Алгоритм перевода чисел из любой системы счисления в десятичную.
Записать данное число в общем виде:
АВСр=А·р2+В·р1+С·р0
Найти сумму ряда. Полученное число является значением числа в 10СС.
100112=1·24+0·23+0·22+1·21+1·20==1910
1448=1·82+4·81+4·80=64+32+4=10010
1С516=1·162+12·161+5·160=256+192+5=45310
Перевод из 2ССв 8СС.
Разбиваем данное число на триады (на группы по три цифры). По таблице смотрим соответствие двоичной и восьмеричной систем счисления.
1 100 101 0112=14538
Перевод из 2ССв 16СС.
Разбиваем данное число на тетрады (на группы по четыре цифры). По таблице смотрим соответствие двоичной и шестнадцатеричной систем счисления.
11 0010 10112=32В16
Операции с числами.
Пример. Пусть р = 5. Вычислить 3445 + 2425.
Решение.
3445
+2425
11415
1) 4 + 2 = 6 = 115: 1 записываем в результат и один "десяток" добавляем к "десяткам"
одного из слагаемых.
2) 4 + 4 +1 = 9 = 145: 4 записываем в результат и одну "сотню" добавляем к "сотням"
одного из слагаемых.
3).3 + 2 + 1 =6 = 115: записываем в результат.
Получаем: 3445 + 2425 = 11415.
Пример.
101102
+1110112
10100012
Пример.
1101112
+1011012
11001002
Как производятся арифметические операции в позиционных системах счисления?
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
Таблицы сложения легко составить, используя Правило Счета.
Сложение в двоичной системе

|
Сложение в восьмеричной системе
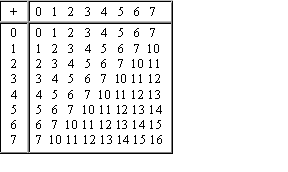
|
Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
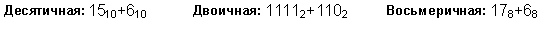
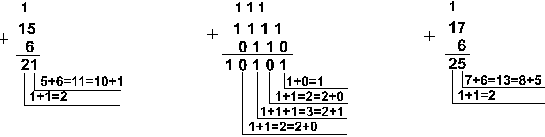
Шестнадцатеричная: F16+616
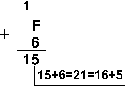
|
Ответ: 15+6 = 2110 = 101012 = 258 = 1516.
Проверка. Преобразуем полученные суммы к десятичному виду:
101012 = 24 + 22 + 20 = 16+4+1=21,
258 = 2 . 81 + 5 . 80 = 16 + 5 = 21,
1516 = 1 . 161 + 5 . 160 = 16+5 = 21.
|
Пример 2. Сложим числа 15, 7 и 3.
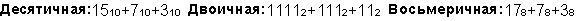
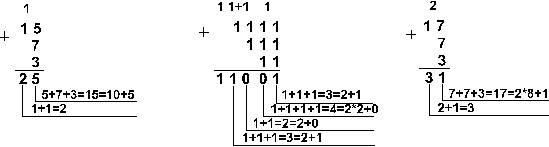
Шестнадцатеричная: F16+716+316
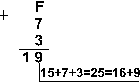
|
Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916.
Проверка:
110012 = 24 + 23 + 20 = 16+8+1=25,
318 = 3 . 81 + 1 . 80 = 24 + 1 = 25,
1916 = 1 . 161 + 9 . 160 = 16+9 = 25.
|
Пример 3. Сложим числа 141,5 и 59,75.
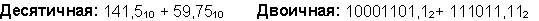
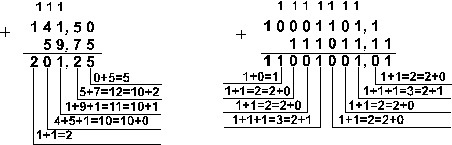
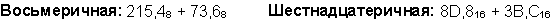
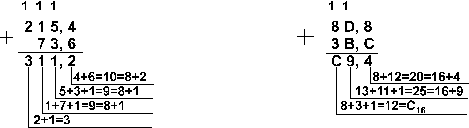
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25
311,28 = 3 . 82 + 181 + 1 . 80 + 2 . 8-1 = 201,25
C9,416 = 12 . 161 + 9 . 160 + 4 . 16-1 = 201,25
В ы ч и т а н и е
Пример 4. Вычтем единицу из чисел 102, 108 и 1016
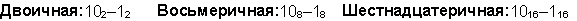
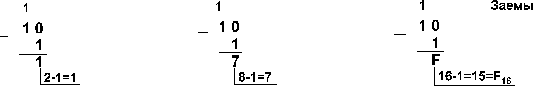
Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016.
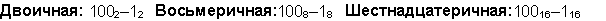
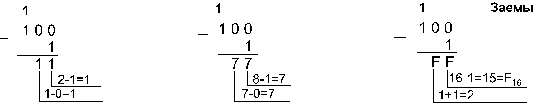
Пример 6. Вычтем число 59,75 из числа 201,25.
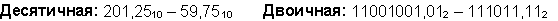
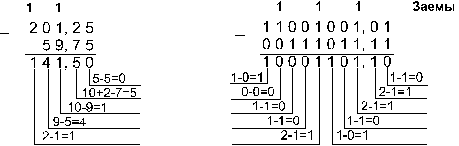
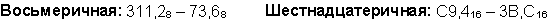

Ответ: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2 . 82 + 1 . 81 + 5 . 80 + 4 . 8-1 = 141,5;
8D,816 = 8 . 161 + D . 160 + 8 . 16-1 = 141,5.
У м н о ж е н и е
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе

|
Умножение в восьмеричной системе
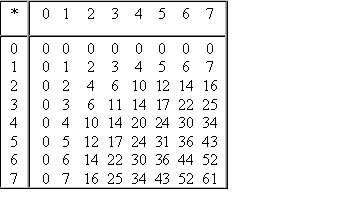
|
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример 7. Перемножим числа 5 и 6.
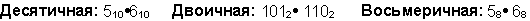
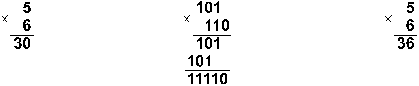
Ответ: 5 . 6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30;
368 = 381 + 680 = 30.
Пример 8. Перемножим числа 115 и 51.
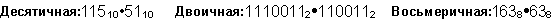
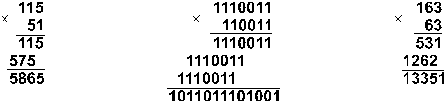
Ответ: 115 . 51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865;
133518 = 1 . 84 + 3 . 83 + 3 . 82 + 5 . 81 + 1 . 80 = 5865.
Д е л е н и е
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 9. Разделим число 30 на число 6.
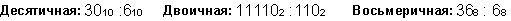
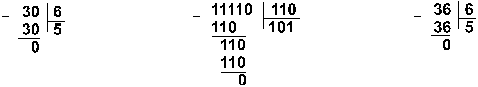
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 10. Разделим число 5865 на число 115.
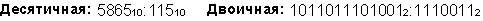
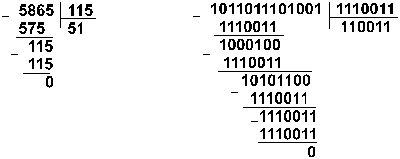
Восьмеричная: 133518 :1638
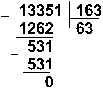
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6 . 81 + 3 . 80 = 51.
Пример 11. Разделим число 35 на число 14.
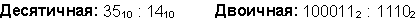

Восьмеричная: 438 : 168
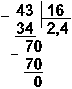
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2 . 80 + 4 . 8-1 = 2,5.
Задание на сопоставление
Решение
Решаем в тетради и будем проверять!
Я даю вам задание, надо преобразовать десятичное целое число в двоичную систему счисления
7,14, 17, 8, 11 и 19
Пример:
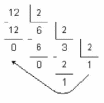
Ответ записывается следующим образом:
1210 =11002
Решение примеров на преобразование десятичных целых чисел в двоичную систему счисления Преобразовать десятичные целые числа в двоичную систему счисления
7,14, 17, 8, 11 и 19
После окончания оценивается каждый ученик, закончивший работу!
Посчитайте баллы за урок и поставьте себе оценку
от 24 до 21 балла – оценка «Отлично»
от 20 до 17 баллов - оценка «Хорошо»
от 16 баллов – оценка «Старайся»
Составить ребусы или загадки на тему «Двоичное кодирование числовой информации в памяти компьютера». На следующем уроке ваши одноклассники будут разгадывать, заданные вами ребусы или загадки.
Двоичная система счисления
1. Задание 1 № 6761
Даны 4 целых числа, записанных в двоичной системе:
10001011; 10111000; 10011011; 10110100.
Сколько среди них чисел, больших, чем 9A16?
Ответ: 3
2. Задание 1 № 6875
Укажите целое число от 8 до 11, двоичная запись которого содержит ровно две единицы. Если таких чисел несколько, укажите наибольшее из них.
Ответ: 10
3. Задание 1 № 7290
Даны 4 целых числа, записанных в различных системах счисления: 3110, F116, 2618, 7118. Сколько среди них чисел, двоичная запись которых содержит ровно 5 единиц?
Ответ: 3
4. Задание 1 № 7661
Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.
Ответ: 1017
5. Задание 1 № 8092
Сколько единиц в двоичной записи восьмеричного числа 17318?
Ответ: 7
6. Задание 1 № 9188
Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 6 нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.
Ответ: 103F
|
Устно отвечают на вопросы, с объяснением.
Находит ошибки в примерах
Каждая группа читает свой параграф, выбирает и предоставляет ключевую информацию из изученного материала.
|
Стратегия
«Верно - не верно»
Словесная оценка учителя.
Взаимооценивание
Стратегия «Стикер»
|
|
Подведение итогов урока (5 мин)
|
Вывод: Человек может складывать, вычитать, умножать, делить, возводить в степень, а компьютер – только складывать, используя дополнительный код, что увеличивает скорость работы компьютера. Причём так работает вся бытовая техника.
Закончите предложения:
Сегодня я узнал…
На уроке я научился…
Мне было трудно…
Мне было непонятно…
Теперь я знаю, что…
Меня удивило…
Я бы хотел узнать, почему…
|
Ученики показывают умение обосновывать свое понимание
Записывают д.з. в дневники
|
Самооценивание
|
Рефлексивный лист, стикеры
| |
 Скачать 479.58 Kb.
Скачать 479.58 Kb.