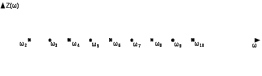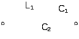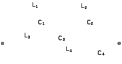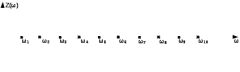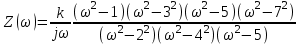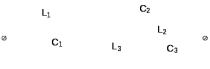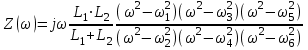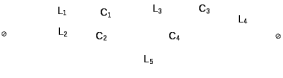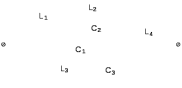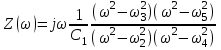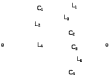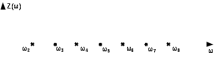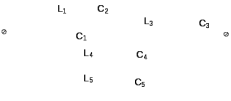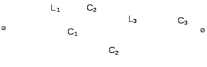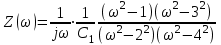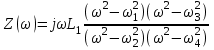База. Двухполюсники УТС. Двухполюсники
 Скачать 1.89 Mb.
|
|
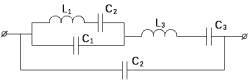
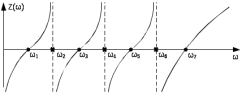
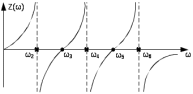
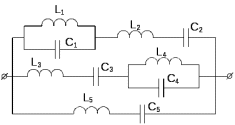
Двухполюсники Задачами теории линейных электрических цепей является установление или обеспечение связей между напряжениями и токами в раненых частях электрической цепи. Новая техника требует точных методов расчета, которые основываются на теории линейных электрических цепей. В задачу теории цепей входит изучение совместного действия всех образующих цепей элементов. Электрические цепи с двумя зажимами состоящие из катушек и конденсаторов, без потерь называются реактивными двухполюсниками. Сложность двухполюсника определяется числом входящих в него элементов. Различают двухполюсники одноэлементные, двухэлементные, трехэлементные и т.д. Число элементов в двухполюснике считается по числу конденсаторов и катушек, остающихся после возможного упрощения схемы.  Z = jωL Z = 1/(jωC) = -j(1/ωC) (1.1)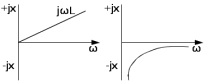 Рис.1. Одноэлементные двухполюсники и графики зависимости их сопротивлений от частоты Свойства реактивного двухполюсника может характеризовать график Z(ω) - частотная зависимость сопротивления.  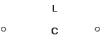 Рис. 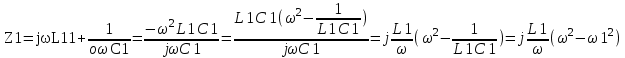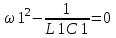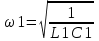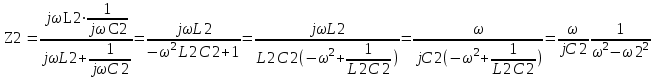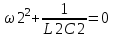2 Схемы двухэлементных двухполюсников    - резонанс напряжений (1.2)  (1.3) Выражения (1.2) и (1.3) для сопротивления двухэлементных двухполюсников характеризуется зависимостью этих сопротивлений от частоты. Графические зависимости Z1(ω) рис 2а и Z2(ω) рис 2б. 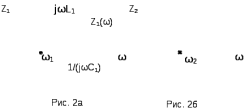 ω1 – частота резонанса напряжений ω2 – частота резонанса токов Рис. 2а и 2б Графические зависимости Z1(ω) рис 2а и Z2(ω) рис 2б. Из трех реактивных элементов можно составить четыре различных схем двухполюсников рис.3 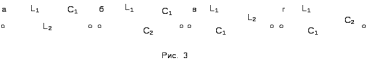 Рис. 3 Трехэлементные двухполюсникиТрехэлементные двухполюсники образуют попарно две группы. Например, двухполюсники а, в пропускают постоянный ток и обладают при больших частотах большим сопротивлением. Двухполюсники б, г не пропускают постоянного тока и обладают малым сопротивлением при высоких частотах. 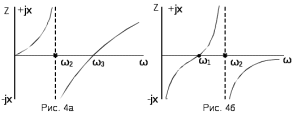 Рис. 4 Графики сопротивления для трехэлементные двухполюсниках этих двух типов Общие свойства реактивных двухполюсников, эквивалентные и обратные двухполюсники. Число резонансов любого реактивного двухполюсника на конечных частотах на единицу меньше числа элементов в нем (с учетом того, что на частотах ω = 0 и ω=∞ сопротивление и проводимость равны 0 или ∞ велики, считают, что на оси частот 0 ≤ ω ≤ ∞ число резонансов на единицу больше числа элементов) Для любого реактивного двухполюсника существует взаимообратный и эквивалентный двухполюсник Зависимость сопротивления любого двухполюсника от частоты можно представить формулой Фостера 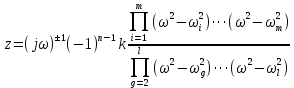 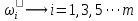 – резонансы напряжения – 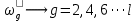резонансы токовЗнак «+» - если схема пропускает постоянный ток Знак «-» - если не пропускает N - число элементов двухполюсника K – определяется из проведения двухполюсника при ω→∞ путем разрыва некоторых катушек или короткого замыкания некоторых конденсаторов, но так чтобы оставался путь для прохождения тока между зажимами двухполюсника Эквивалентные двухполюсники Эквивалентные двухполюсники – это двухполюсники, у которых Z1 = Z2 на всех частотах. Они имеют разные схемы, но абсолютно одинаковые сопротивления. Потенциально эквивалентные двухполюсники – это двухполюсники схемы которых таковы, что при изменении величины элементов одной из схем (без изменения самих схем) они могут стать эквивалентными. Эти двухполюсники должны отвечать двум условиям: Иметь одинаковое число элементов Одинаковый характер сопротивления при ω = 0 и ω → ∞ Обратные двухполюсники – это двухполюсники, у которых Z1*Z2 = const=R2 на всех частотах, где R – коэффициент образности Потенциально обратные двухполюсники - это двухполюсники схемы которых таковы, что при изменении величины элементов одной из схем (без изменения самих схем) они могут стать обратными. Эти двухполюсники должны отвечать двум условиям: Иметь одинаковое число элементов Противоположный характер сопротивления при ω = 0 и ω → ∞ Таблица 1 Задания для самостоятельного решения
Библиографический список 1. Каллер М.Я. Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи : учебник для вузов ж.-д. транспорта / М. Я. Каллер, Ю. В. Соболев, А. Г. Богданов. - Москва : Транспорт, 1987. - 334 с. 2. Шебес М.Р. Теория линейных электрических цепей в упражнениях и задачах : учебное пособие / М. Р. Шебес. - 2-е изд., перераб. и доп. - Москва : Высшая школа, 1973. - 655 с. 3. Шебес М.Р. Задачник по теории линейных электрических цепей : учебное пособие для студентов электротех. и радиотех. спец. вузов / М. Р. Шебес, М. В. Каблукова. - 4-е изд., перераб. и доп. - Москва : Высшая школа, 1990. - 543 с. 4. Волков Е.А. Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи : учебник для студентов вузов ж.-д. транспорта / Е. А. Волков, Э. И. Санковский, Д. Ю. Сидорович ; под ред. В. А. Кудряшова. - Москва : Маршрут, 2005. 5. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. 6. Каплянский А. Е. и др. Электрические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. -М.: Высш. шк., 1972. -448с. Учебное издание Богданова Елена Сергеевна ТЕОРИЯ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Учебно - практическое пособие для студентов по дисциплине "Теория линейных электрических цепей" для студентов специальности 23.05.05 - "Системы обеспечения движения поездов" всех форм обучения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, 
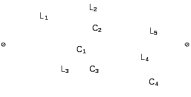
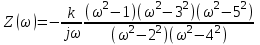
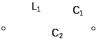
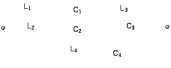
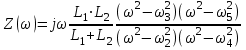
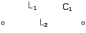
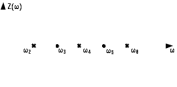
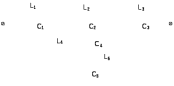
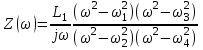
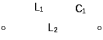
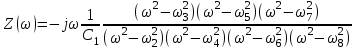
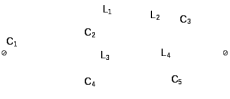
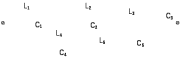
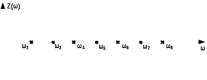
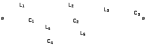
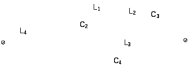
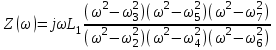
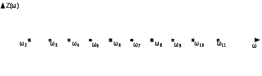
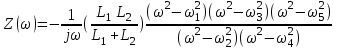
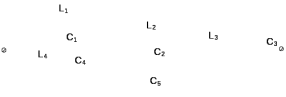
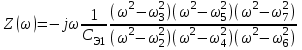