Дз № 3. Векторная алгебра
Сборник задач по математике для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.
№ п/п
|
№ по Еф.
|
Задание
|
Ответ
|
1
|
1.11
|
ABCDEF - правильный шестиугольник, причем 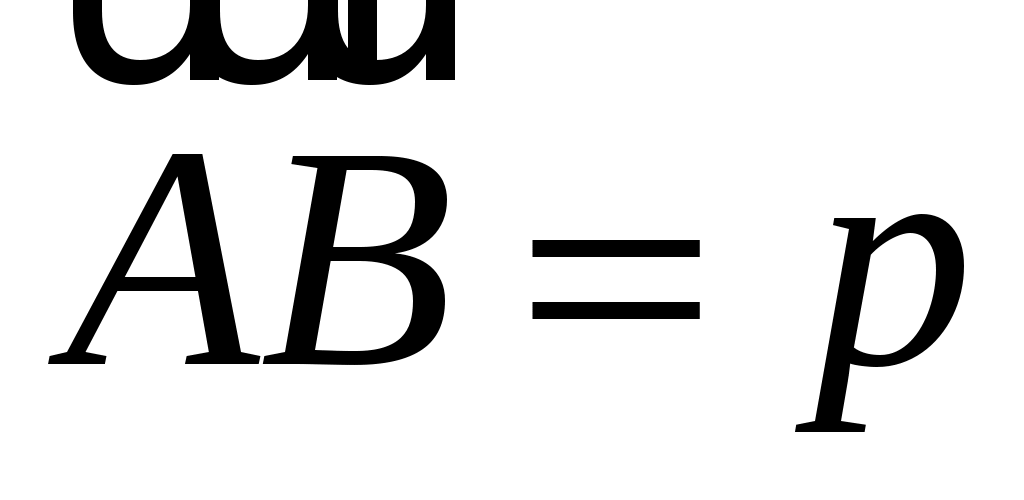 , , 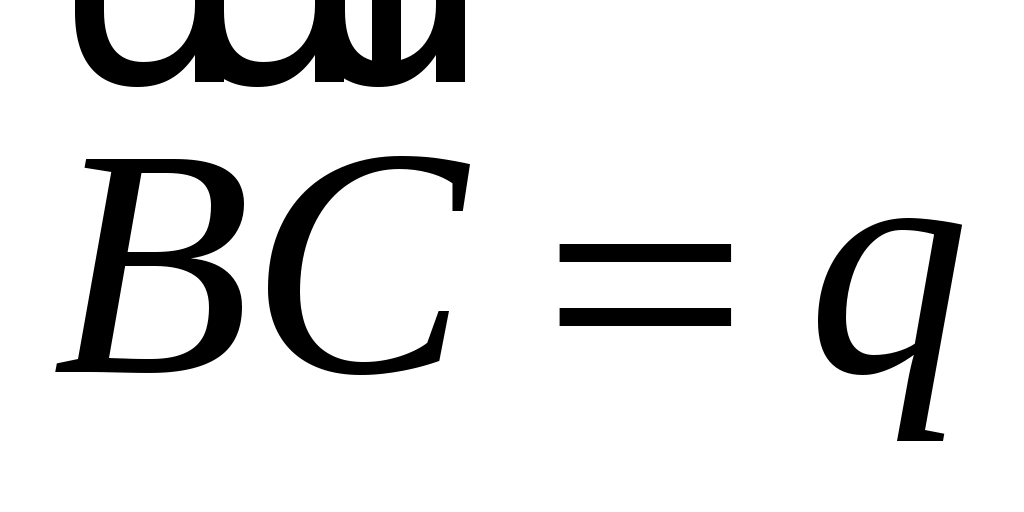 . Выразить через . Выразить через 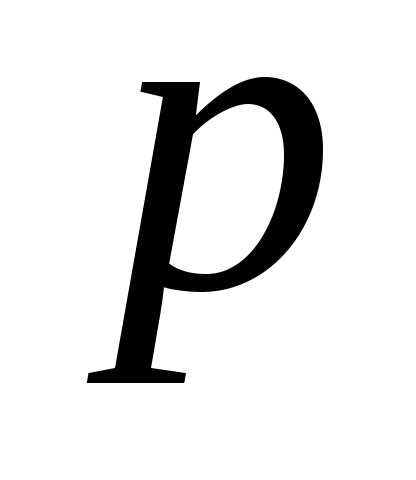 и и 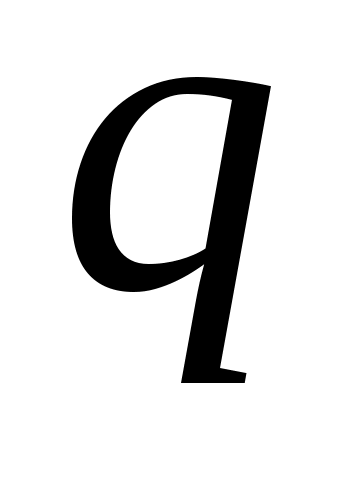 векторы векторы 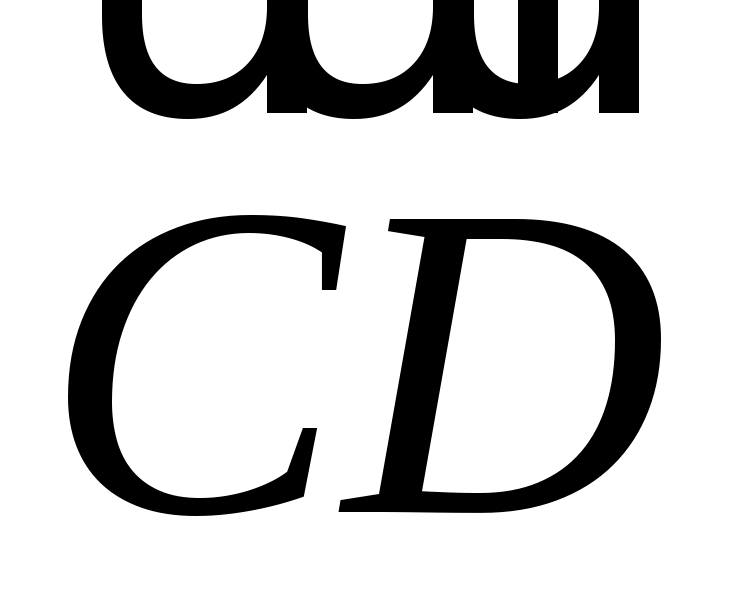 , ,  , , 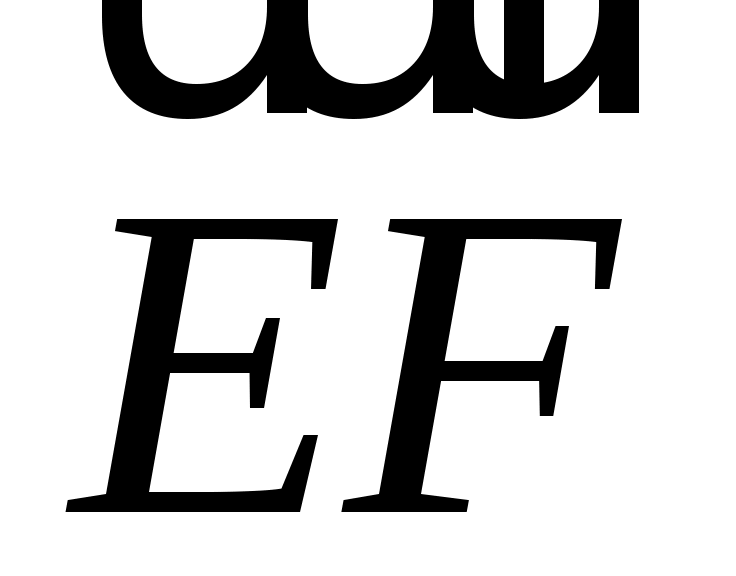 , ,  , , 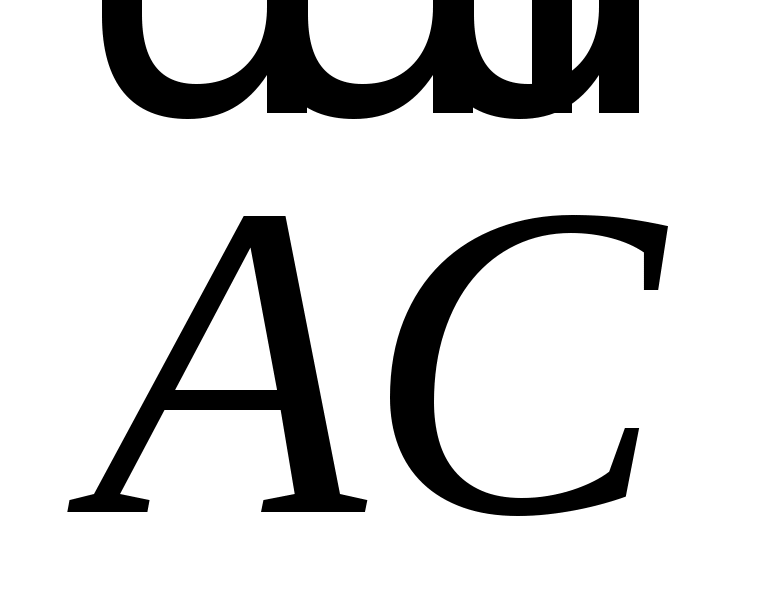 , ,  и и 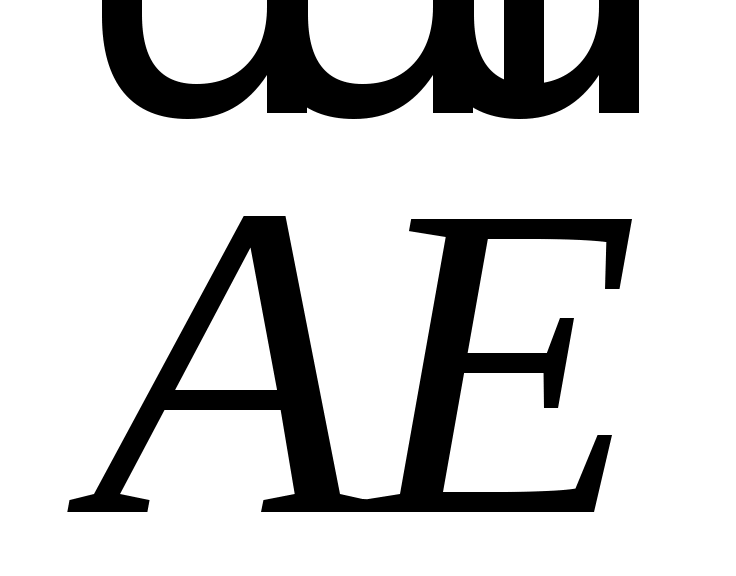 . .
|
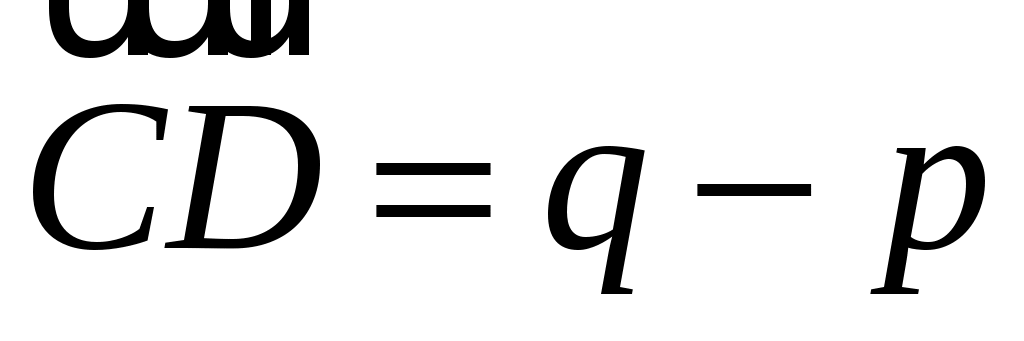 , , 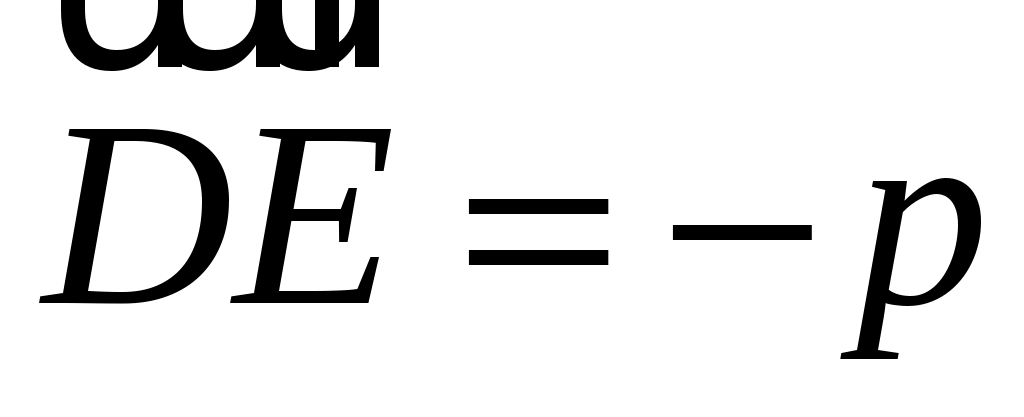 , , 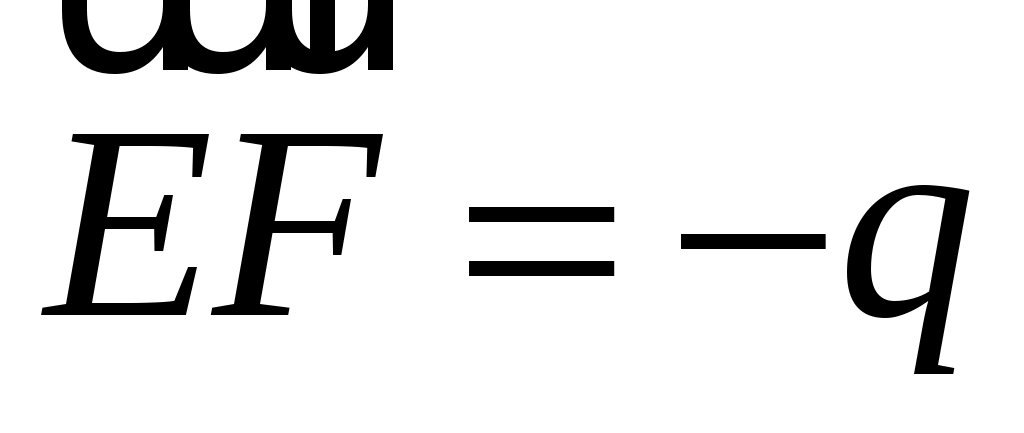 , , 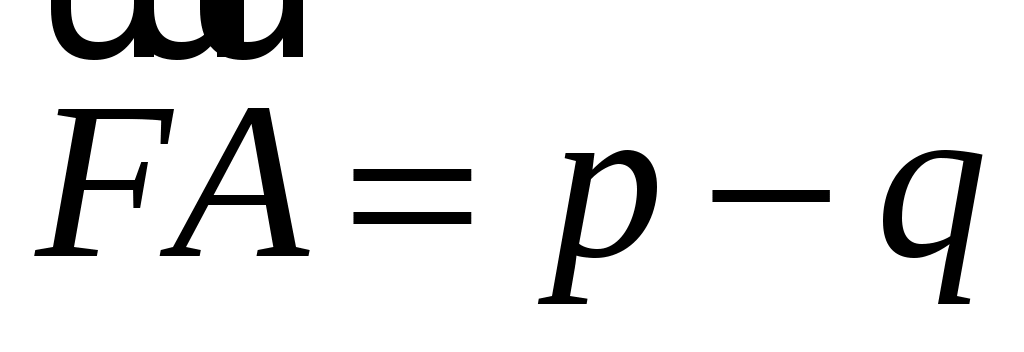 , , 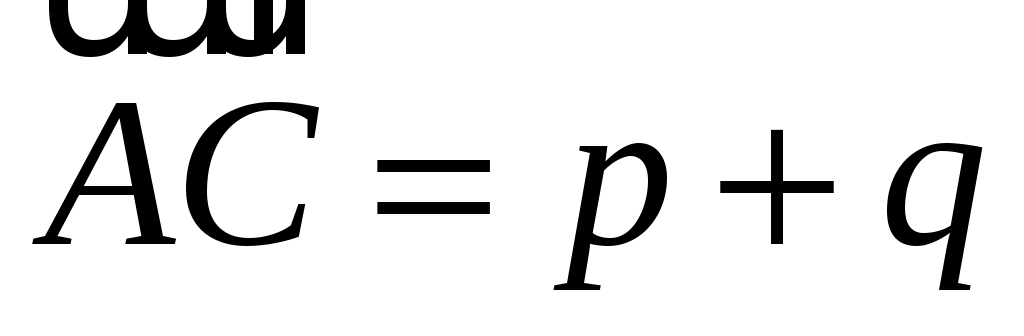 , , 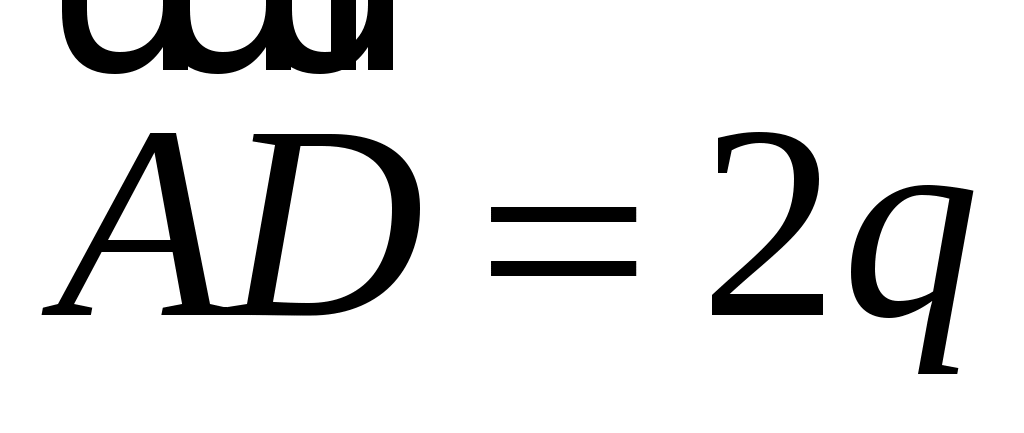 , , 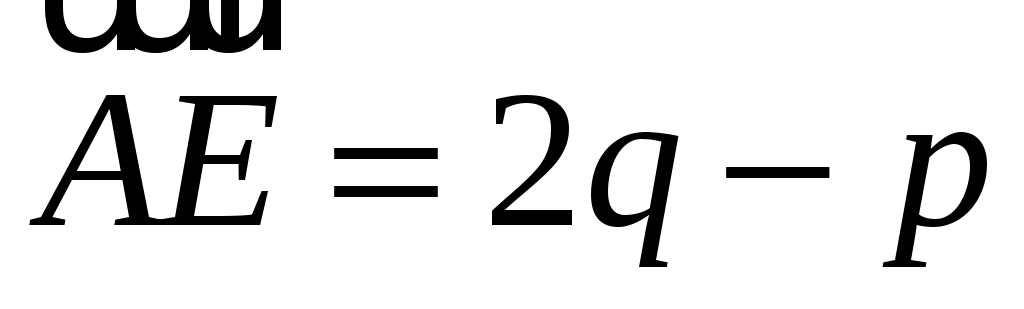 . .
|
2
|
1.18
|
На стороне  параллелограмма параллелограмма 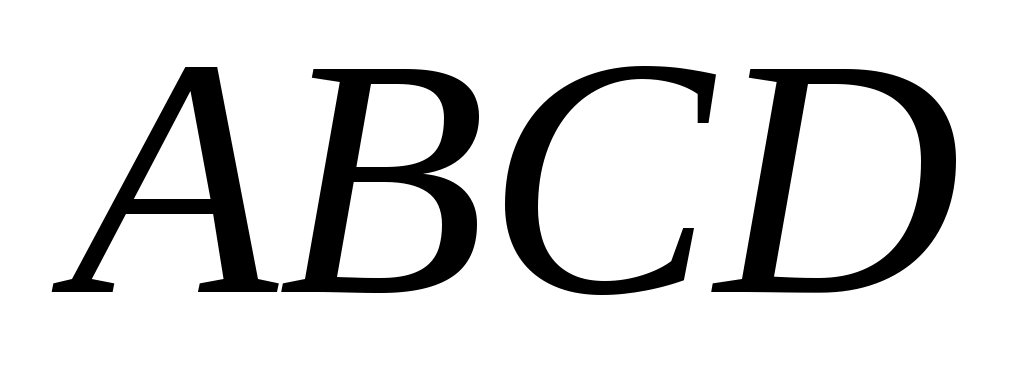 отложен вектор отложен вектор 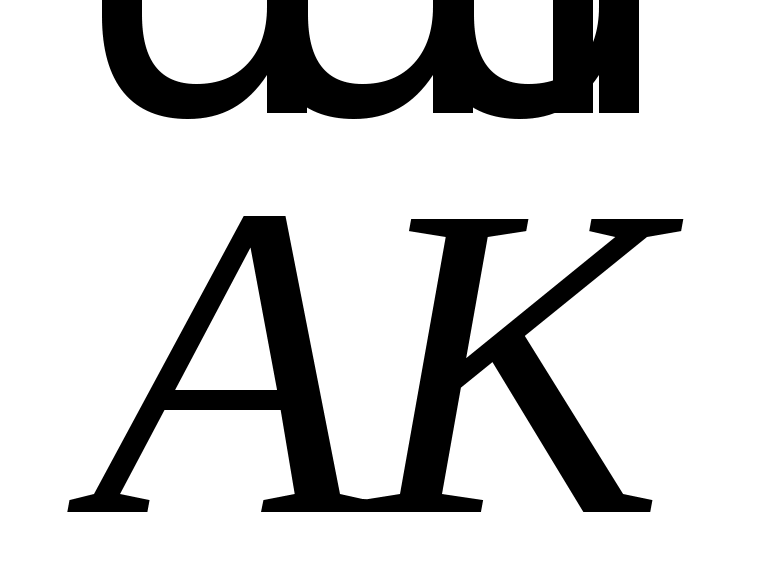 длины длины 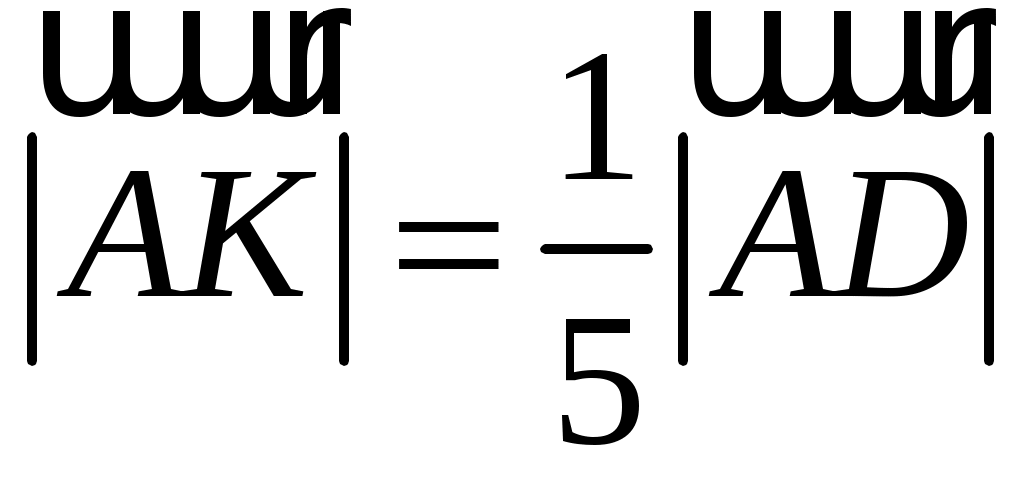 , а на диагонали , а на диагонали 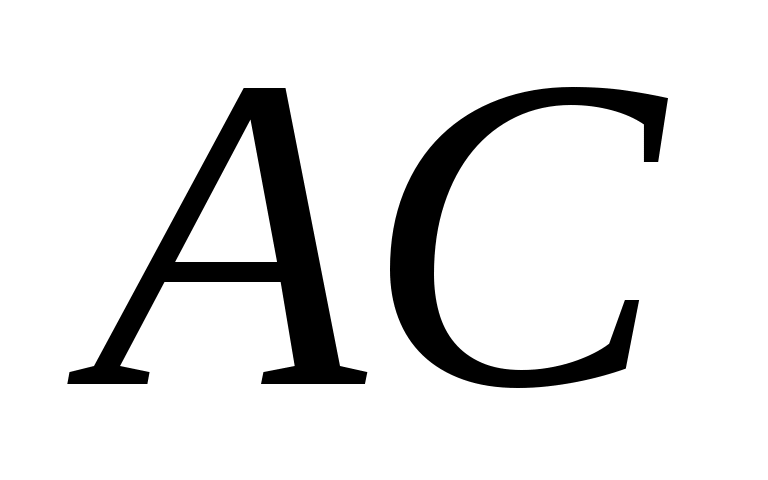 - вектор - вектор  длины длины 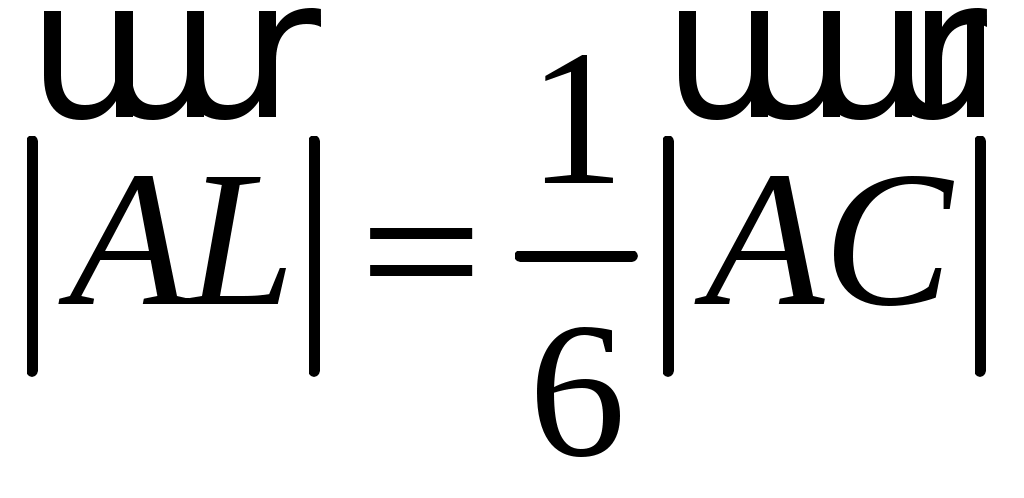 . Доказать, что векторы . Доказать, что векторы 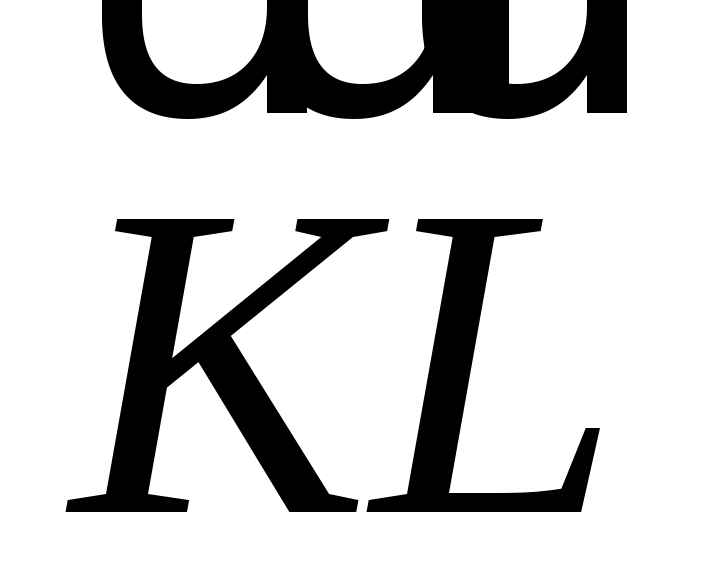 и и 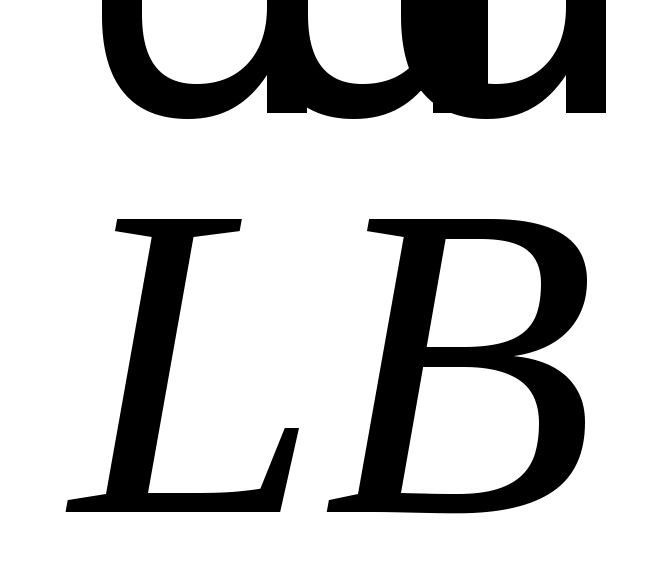 коллинеарны и найти коллинеарны и найти 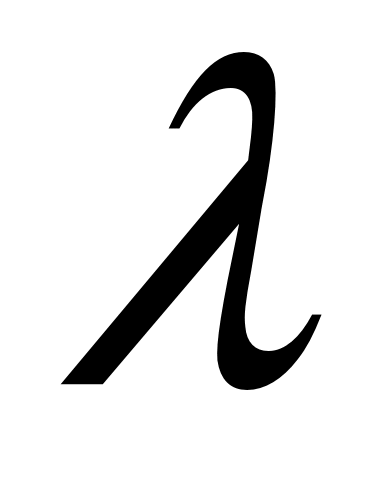 такое, что такое, что 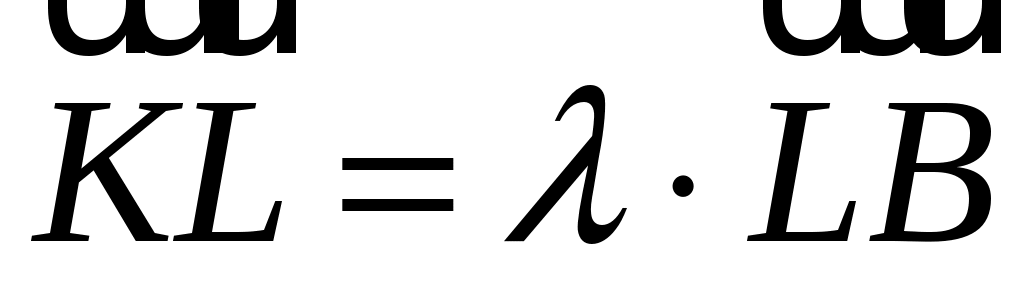 . .
|
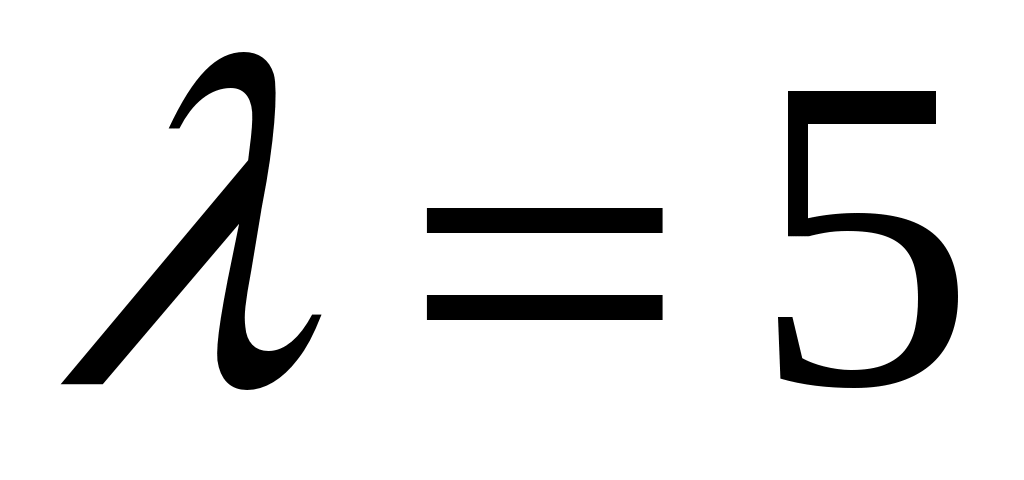
|
3
|
1.19
|
Разложить вектор s = a+b+c по трем некомпланарным векторам:
p = a+b-2c, q = a-b, r = 2b+3c.
|
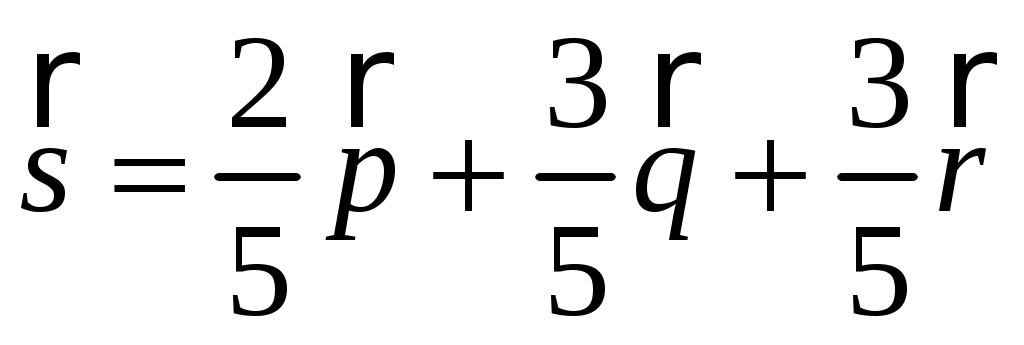
|
4
|
1.27
|
В тетраэдре ОАВС медиана AL грани АВС делится точкой М в отношении 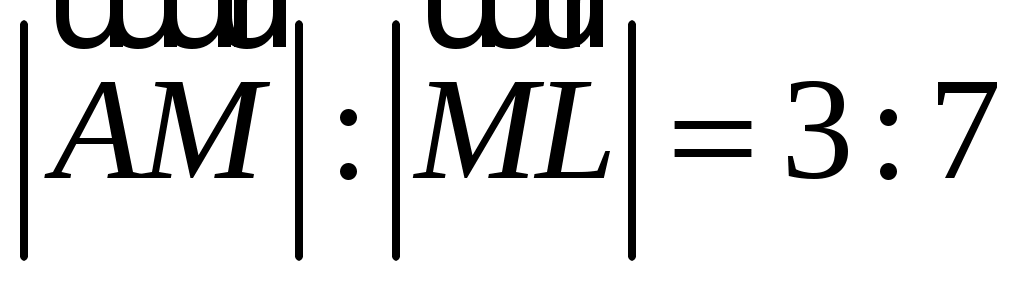 . Найти координаты вектора . Найти координаты вектора 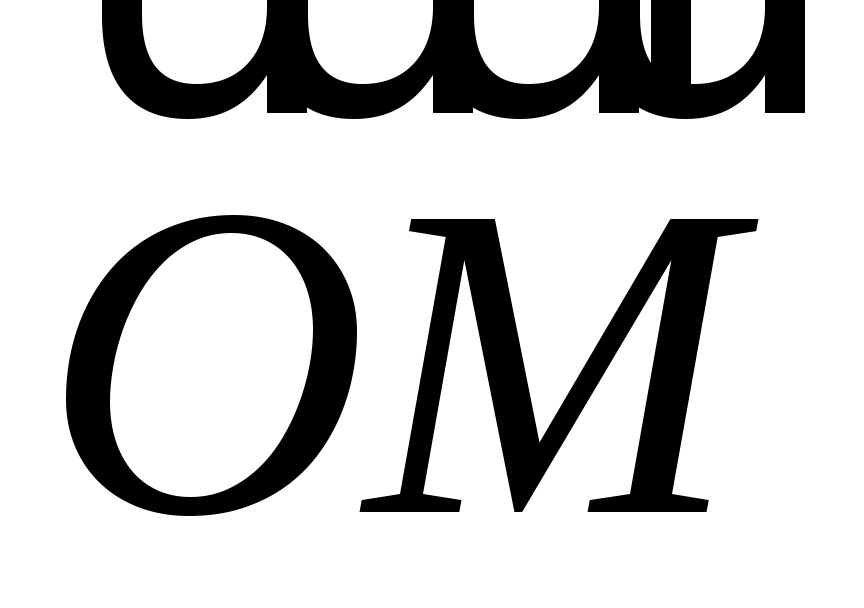 в базисе из ребер в базисе из ребер 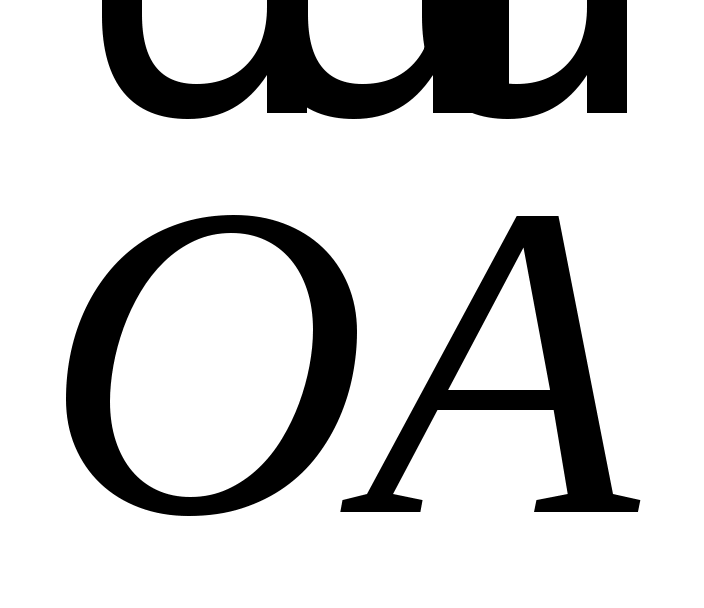 , , 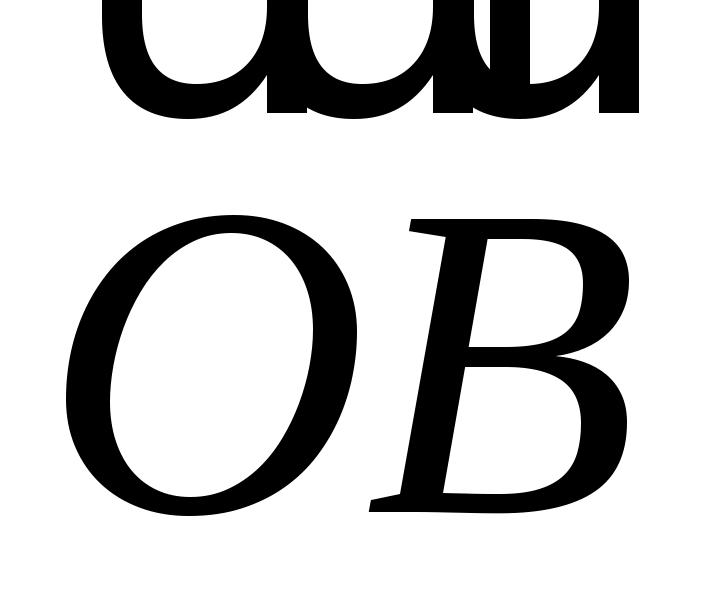 , , 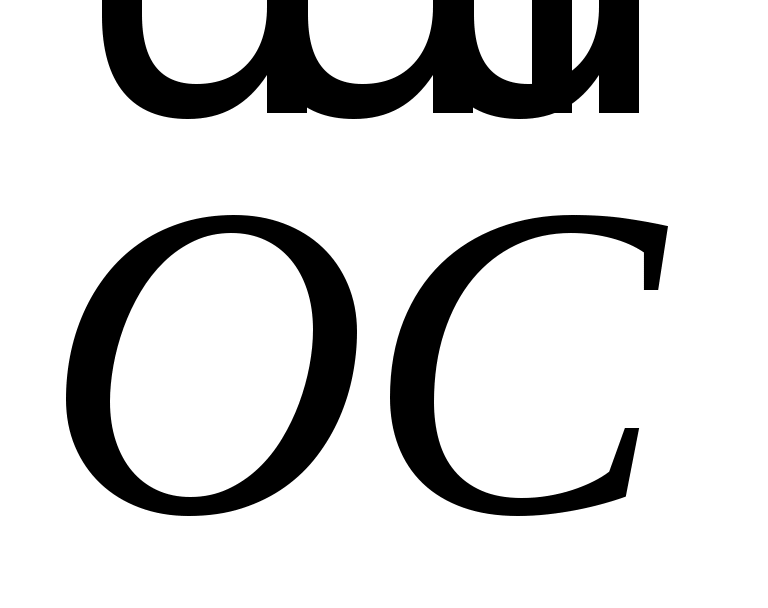 . .
|
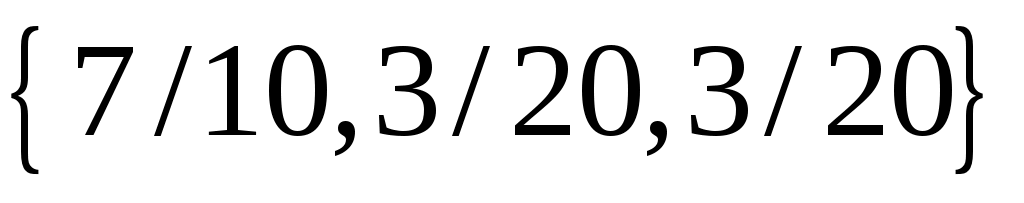
|
5
|
1.35а-г
|
Заданы векторы 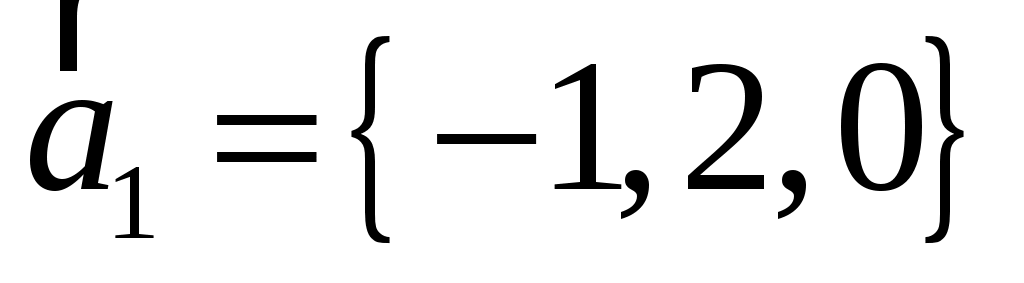 , , 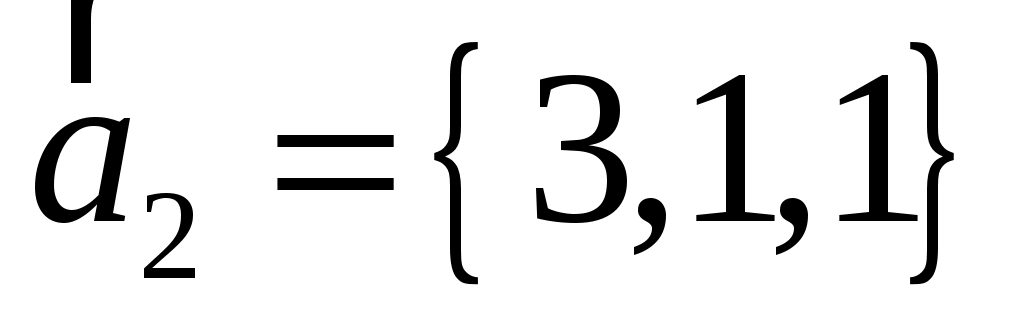 , , 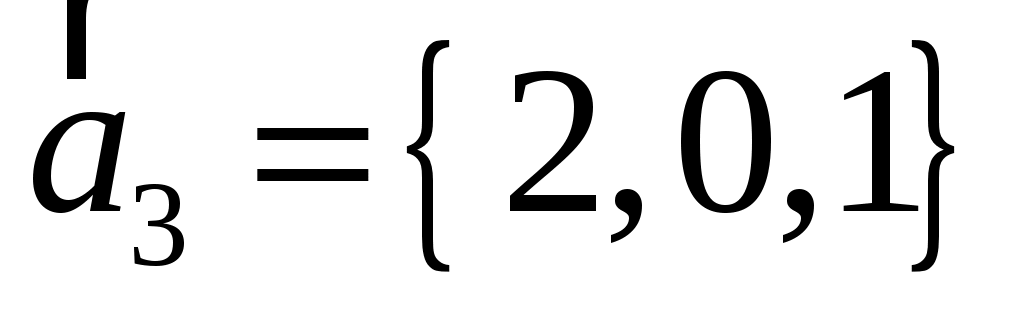 и и 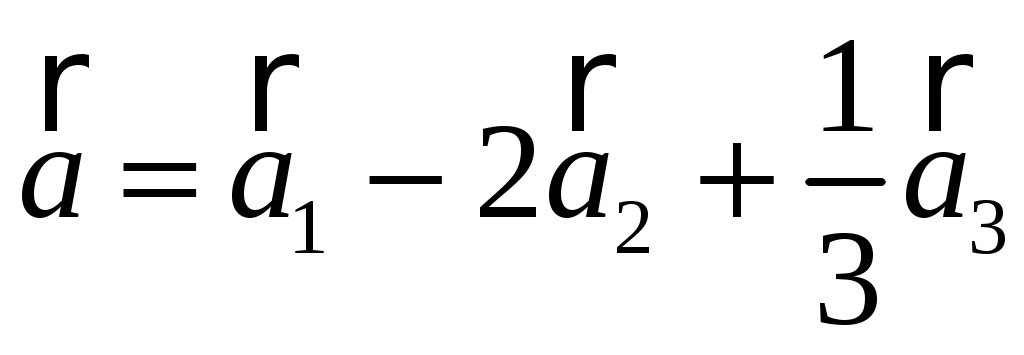 . Вычислить: . Вычислить:
а) 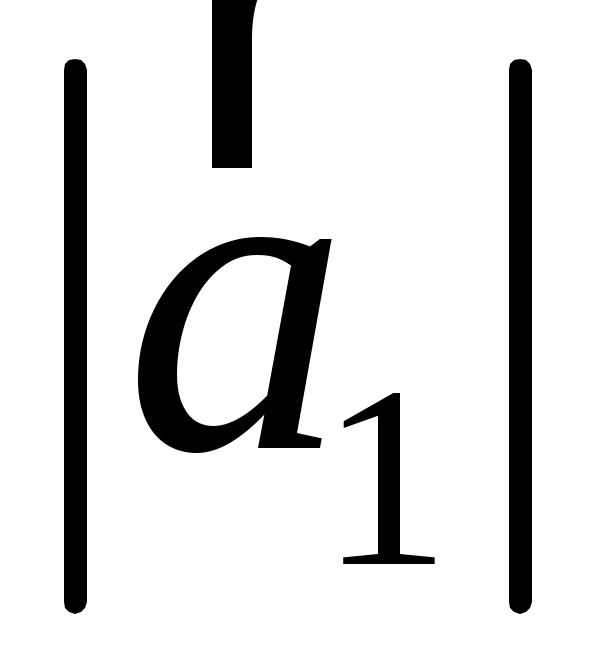 и координаты орта и координаты орта 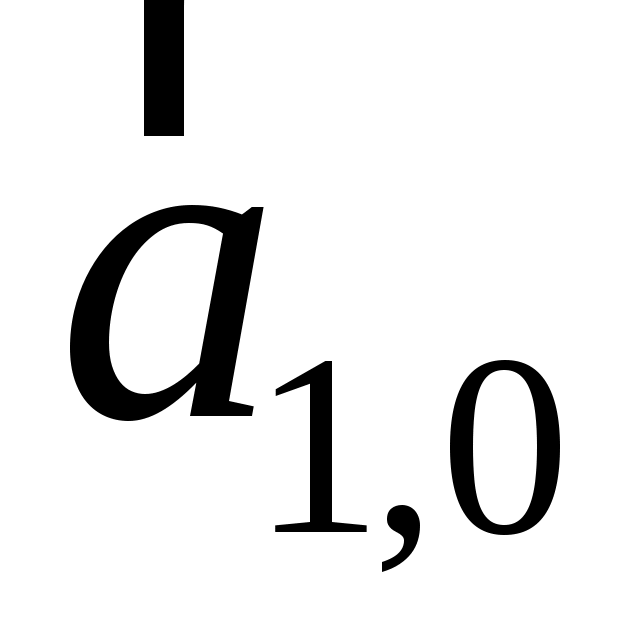 вектора вектора 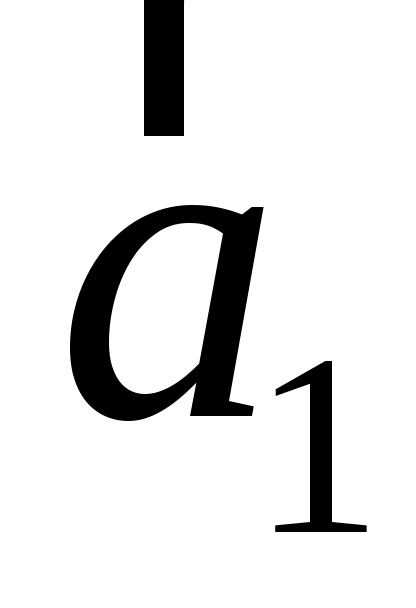 ; б) ; б) 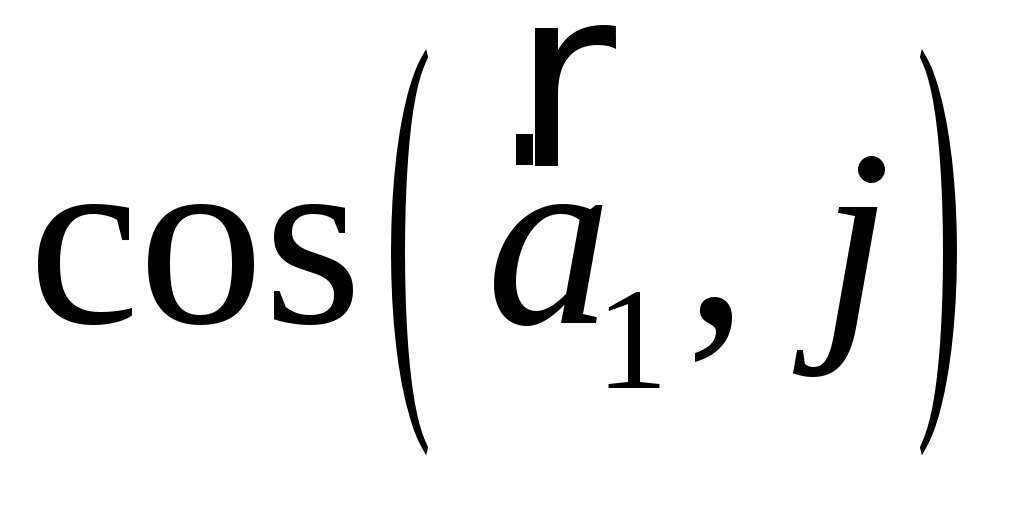 ; ;
в) координату Х вектора 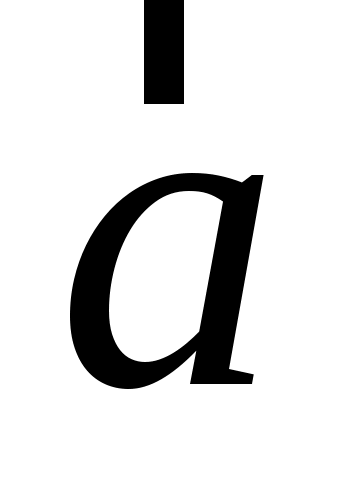 ; г) пр ; г) пр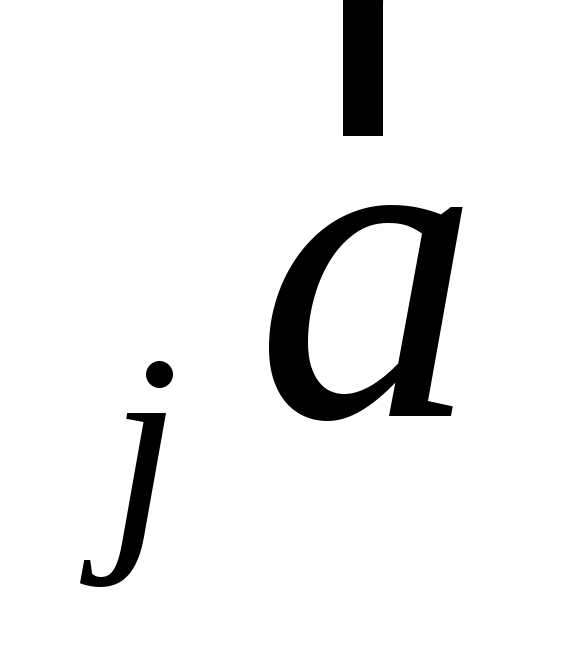 . .
|
а) 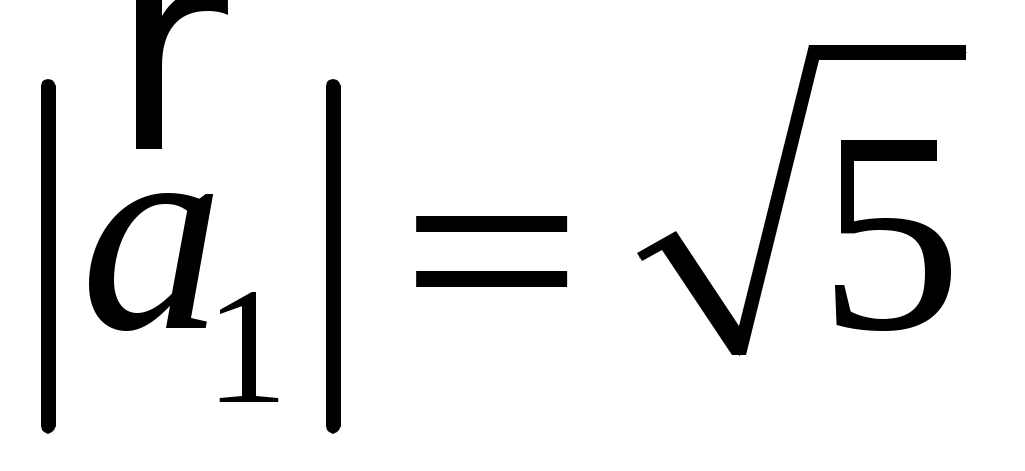 , ,  ; ;
б) 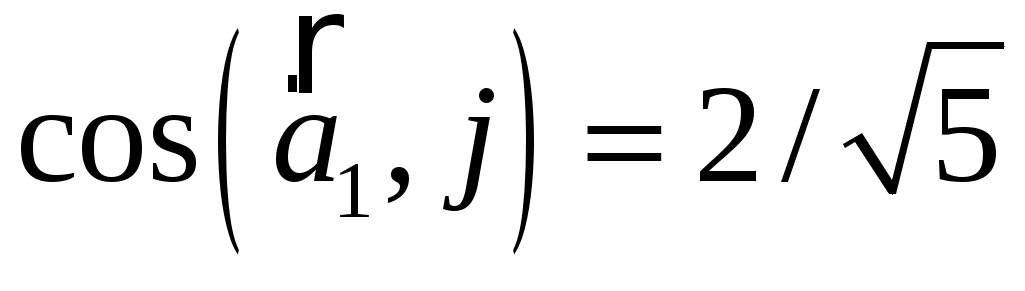 ; ;
в) 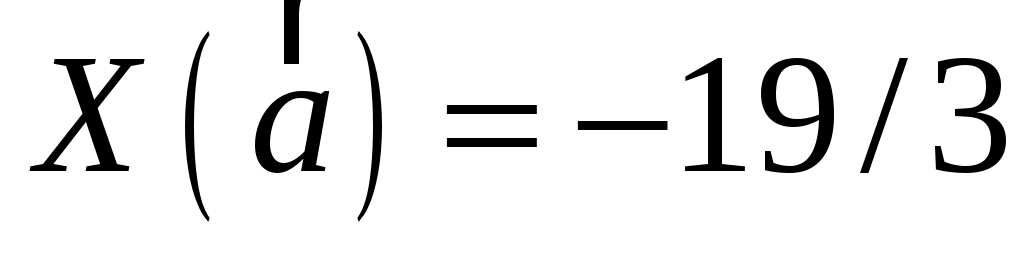 ; ;
г) пр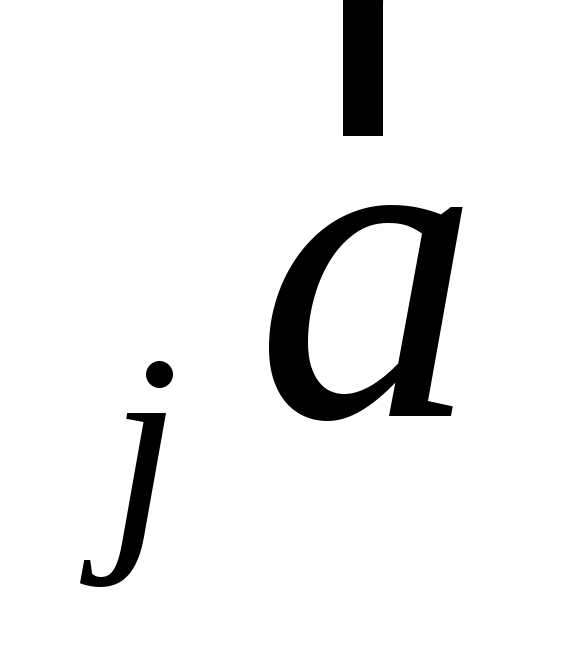 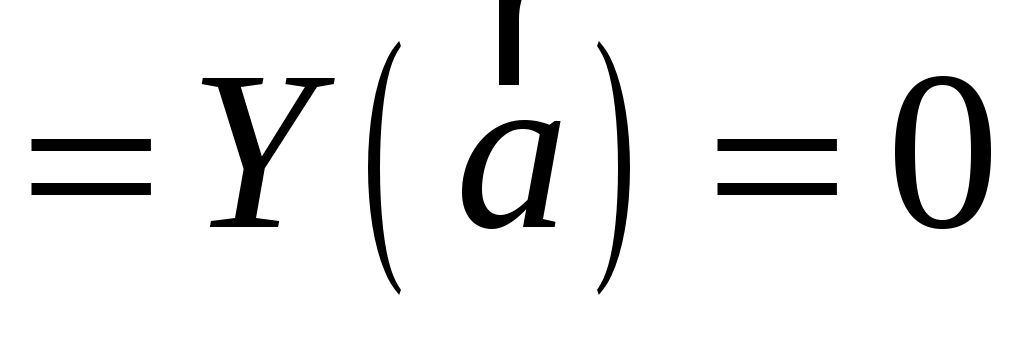
|
6
|
1.39
|
Заданы векторы 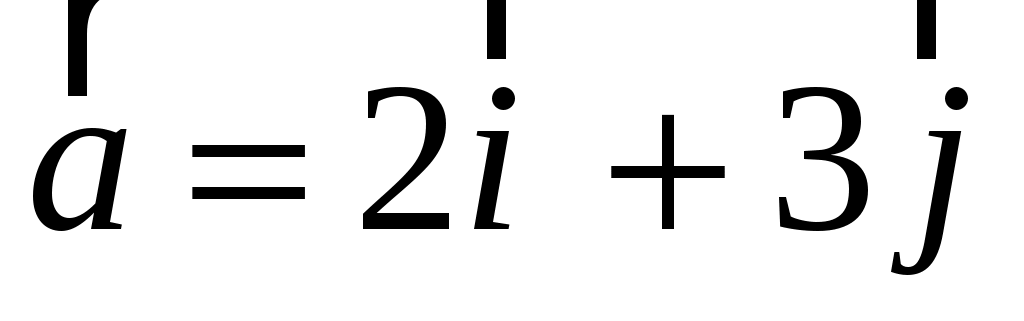 , , 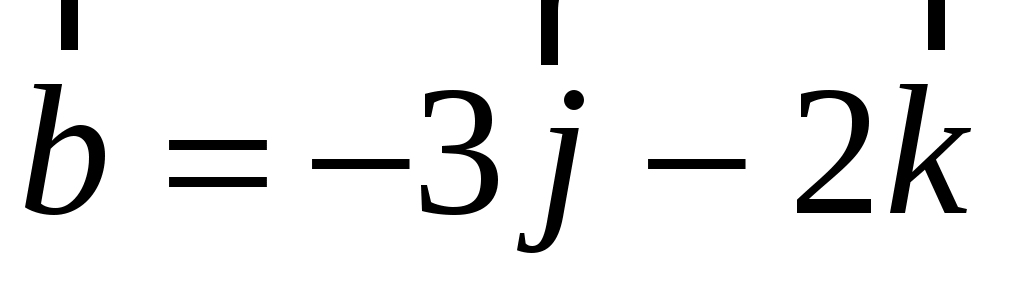 , , 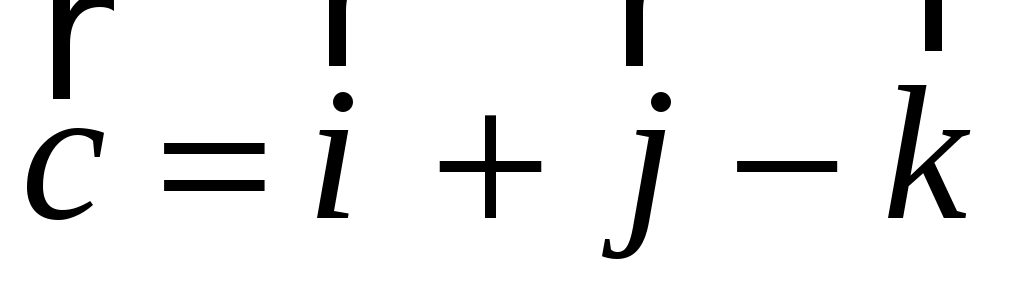 . Найти: . Найти:
а) координаты орта 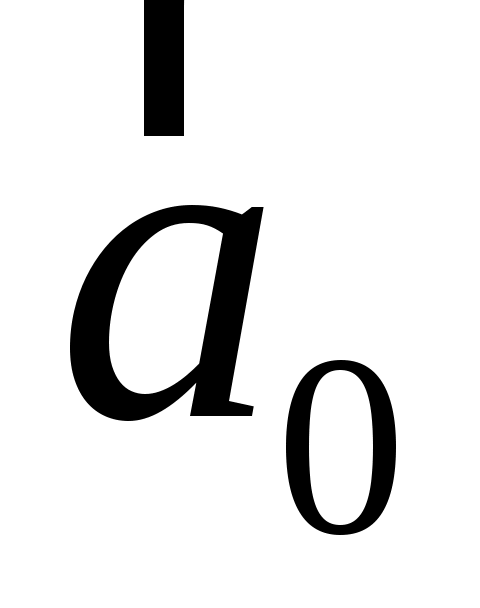 ; ;
б) координаты вектора 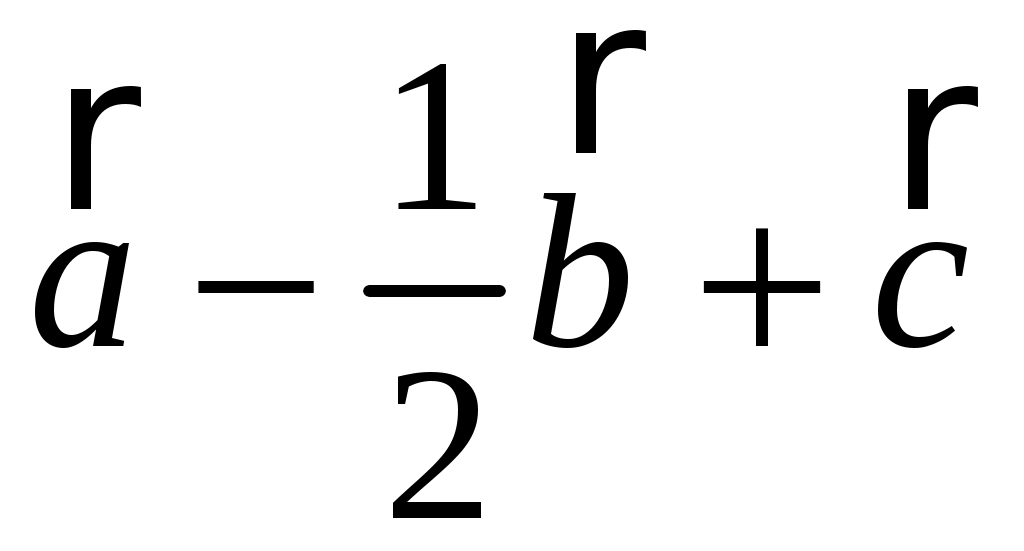 ; ;
в) разложение вектора 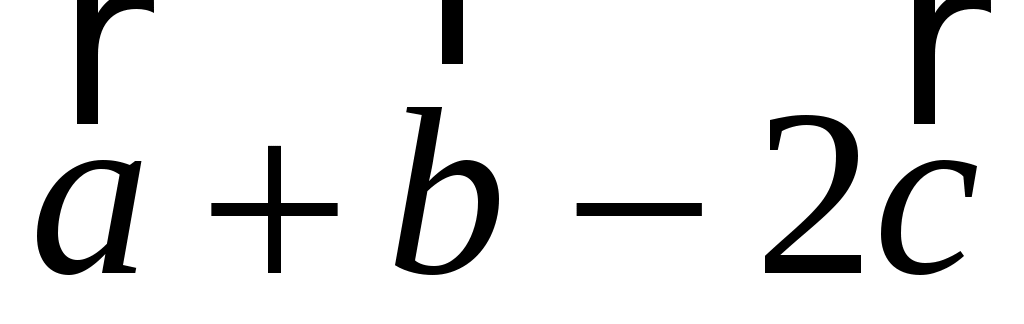 по базису по базису 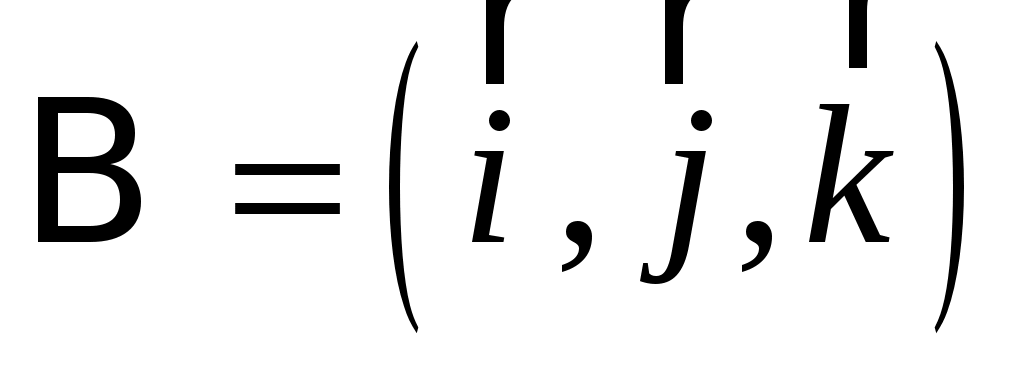 ; ;
г) 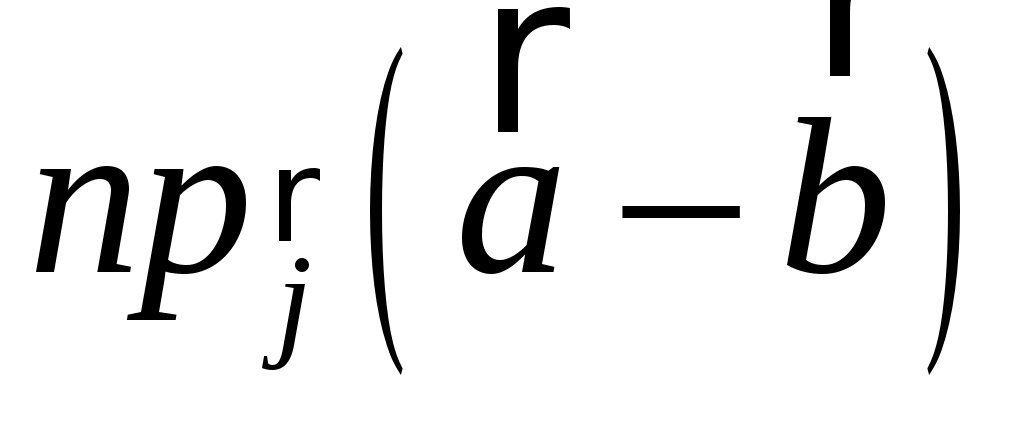 . .
|
а) 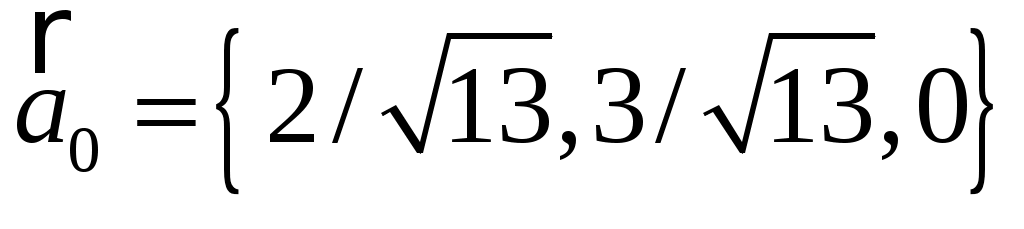 ; ;
б) 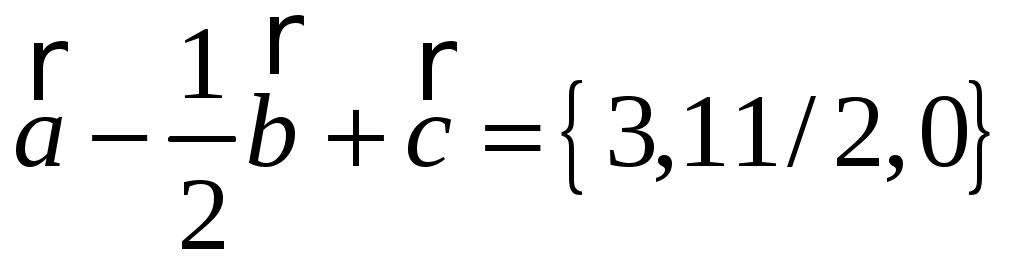 ; ;
в) 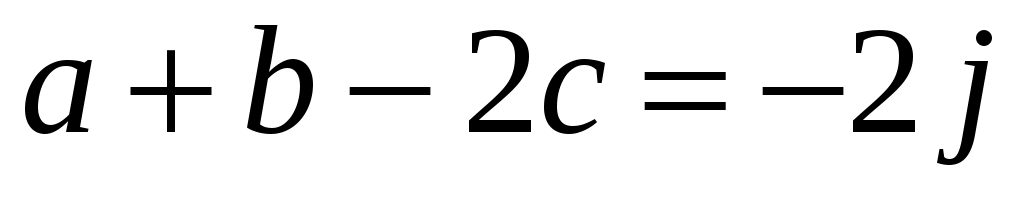 ; ;
г) 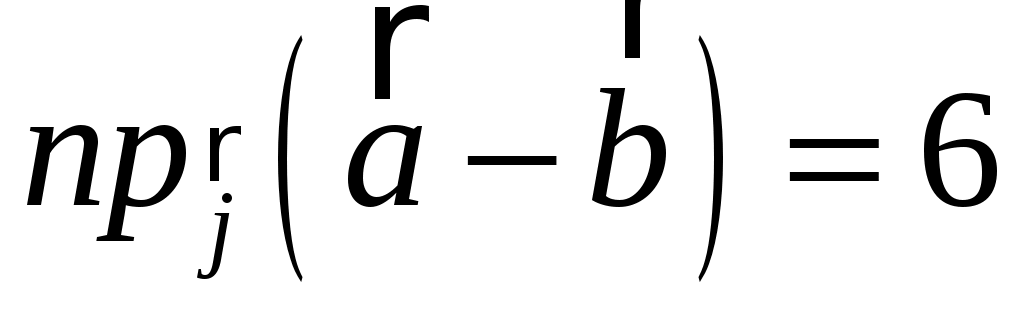 . .
|
7
|
1.43
|
Найти вектор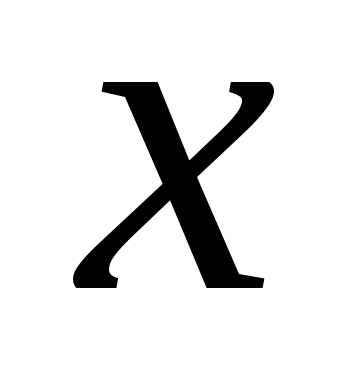 коллинеарный вектору коллинеарный вектору 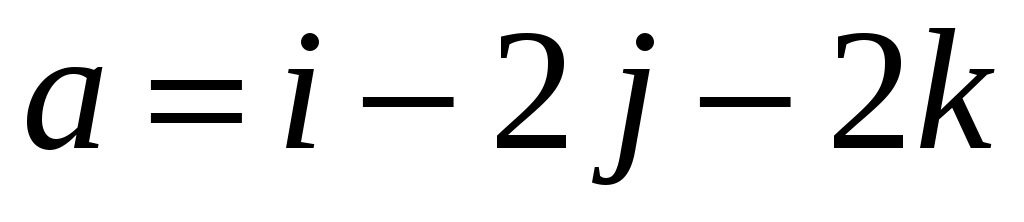 , образующий с ортом j острый угол и имеющий длину , образующий с ортом j острый угол и имеющий длину 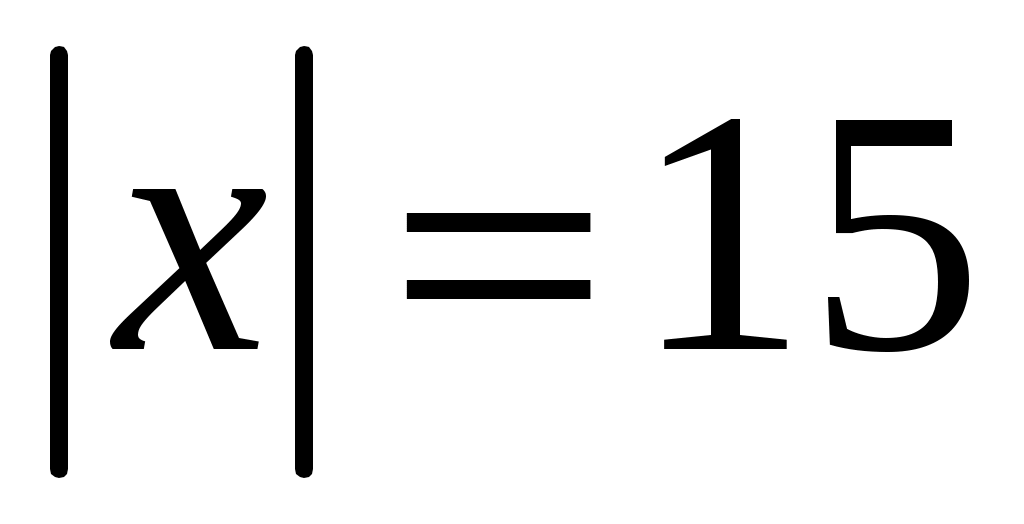 . .
|
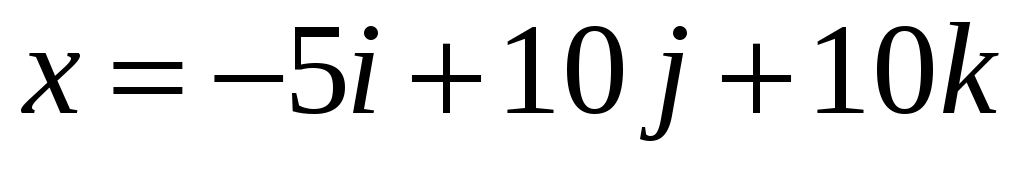
|
8
|
1.44
|
Найти вектор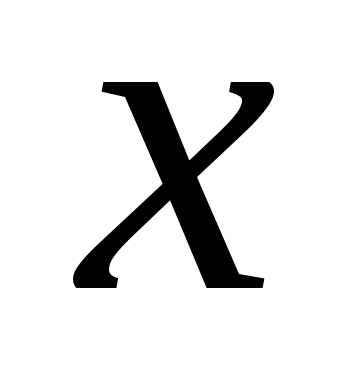 , образующий со всеми тремя базисными ортами равные острые углы, если , образующий со всеми тремя базисными ортами равные острые углы, если 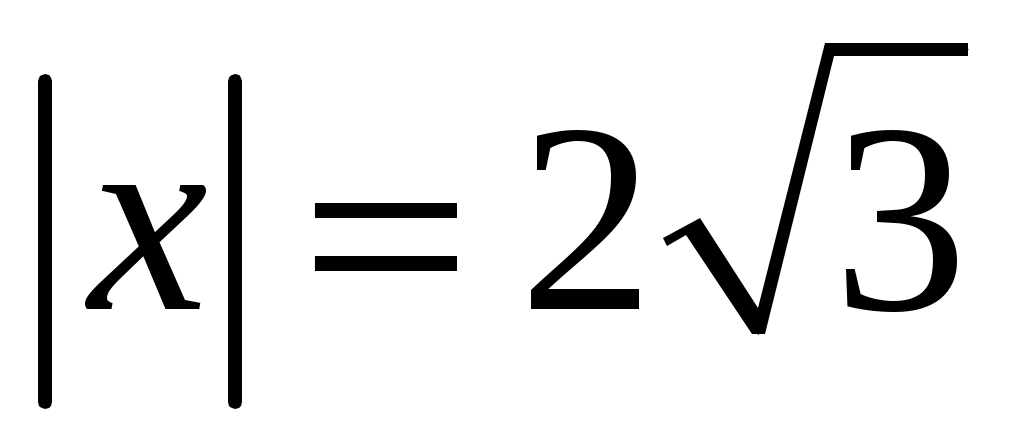 . .
|
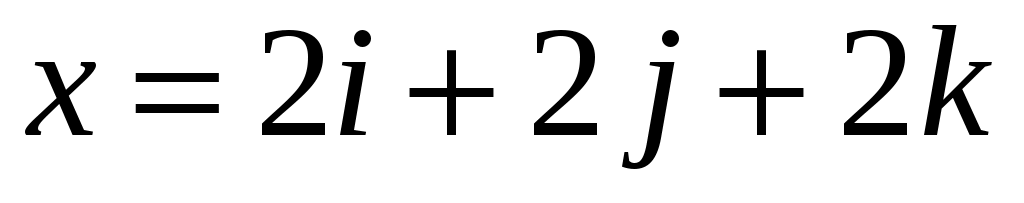
|
9
|
1.46
|
При каких значениях  и и 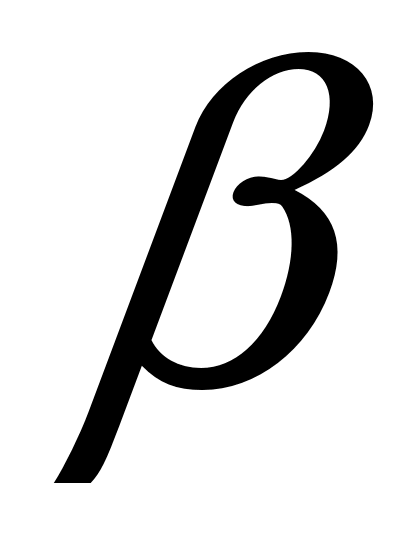 векторы векторы 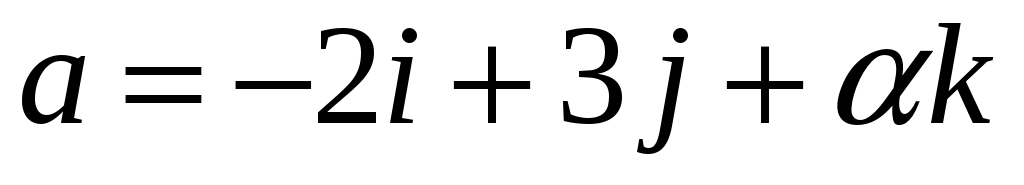 и и 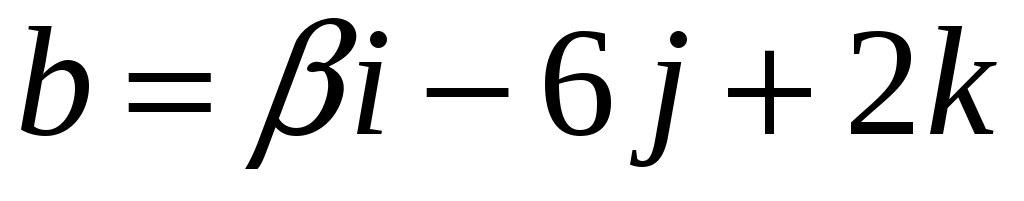 коллинеарны? коллинеарны?
|
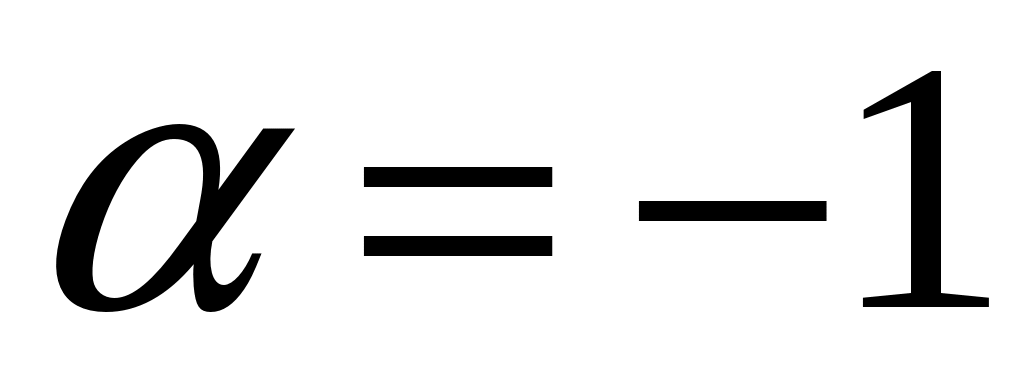 , , 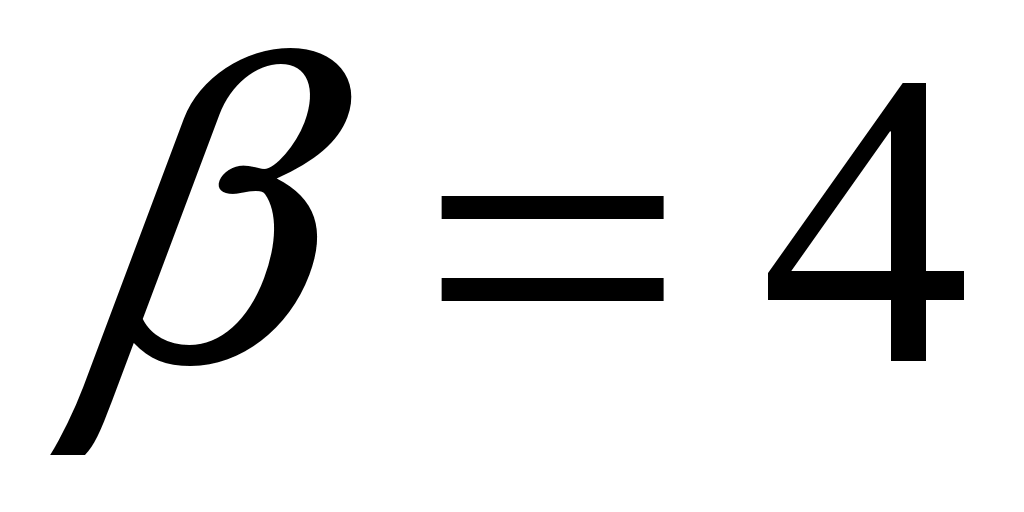
|
10
|
1.38
|
Показать, что тройка векторов 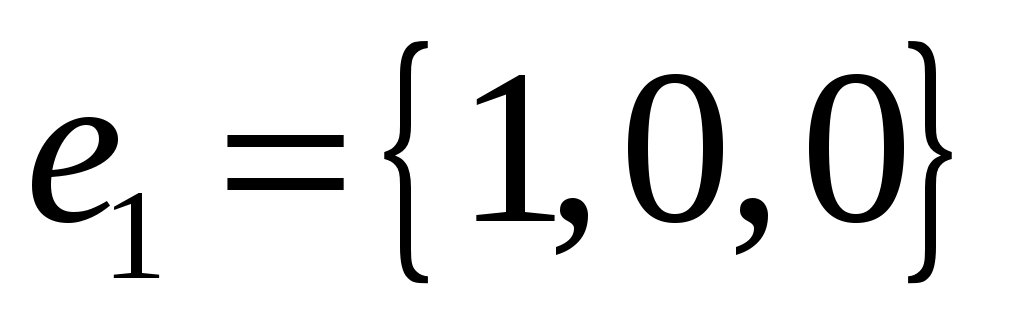 , , 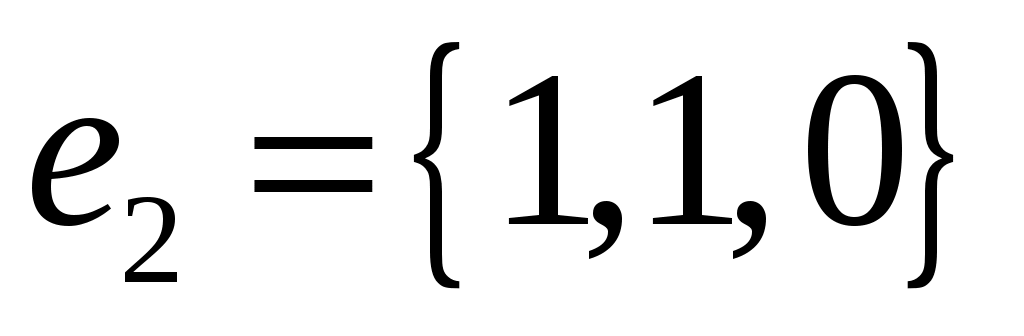 и и 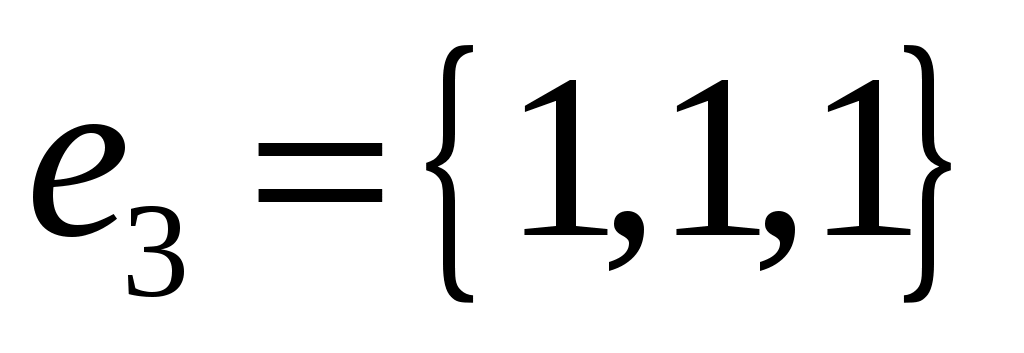 образует базис в множестве всех векторов пространства. Вычислить координаты вектора образует базис в множестве всех векторов пространства. Вычислить координаты вектора 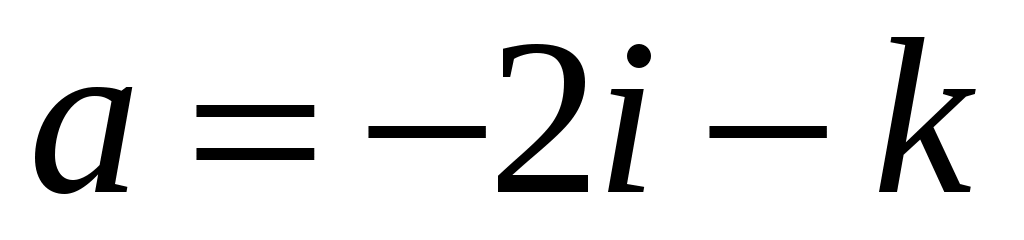 в базисе в базисе 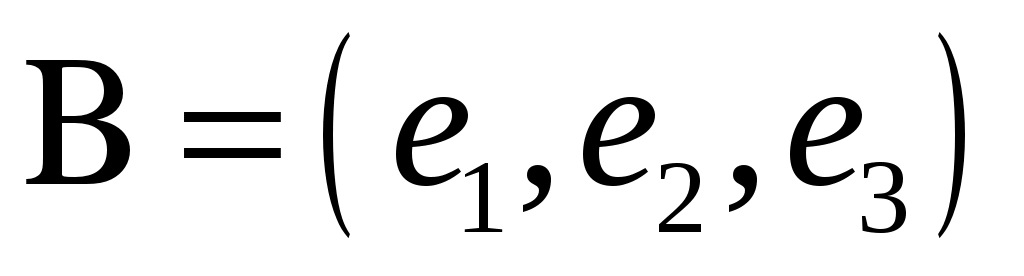 и написать соответствующее разложение по базису. и написать соответствующее разложение по базису.
|
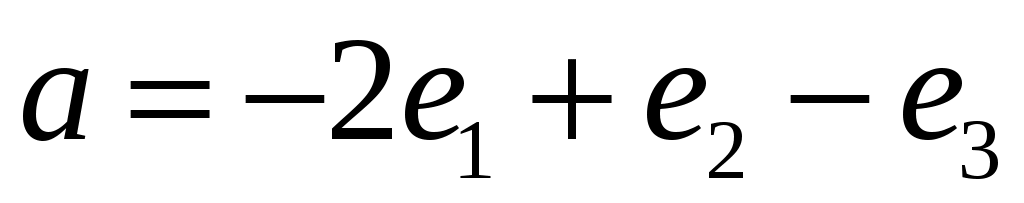
|
11
|
1.65в
|
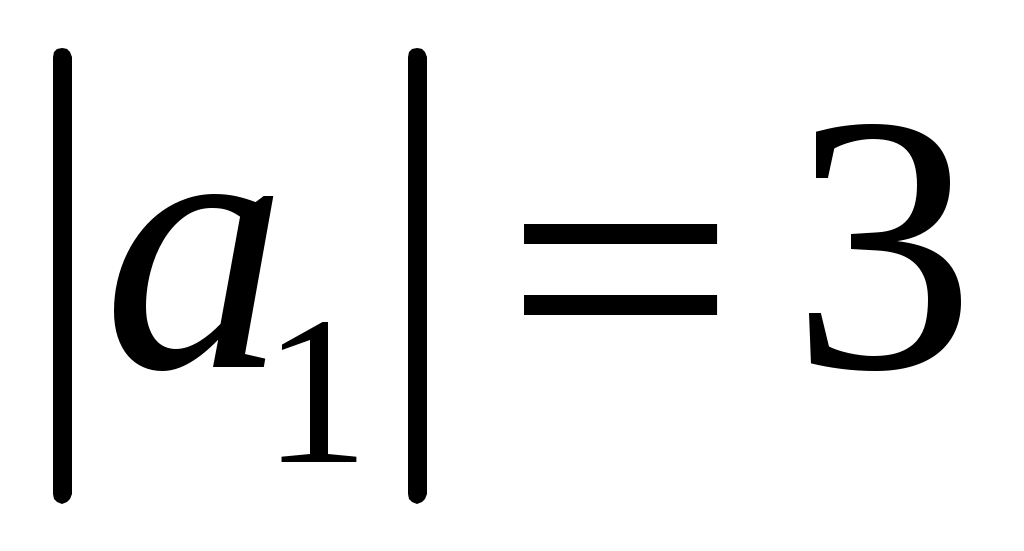 , , 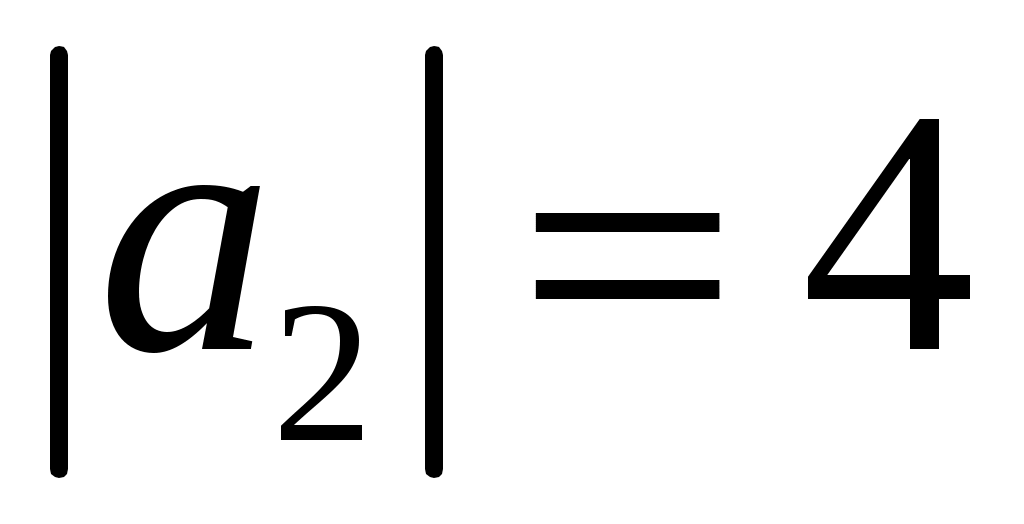 , , 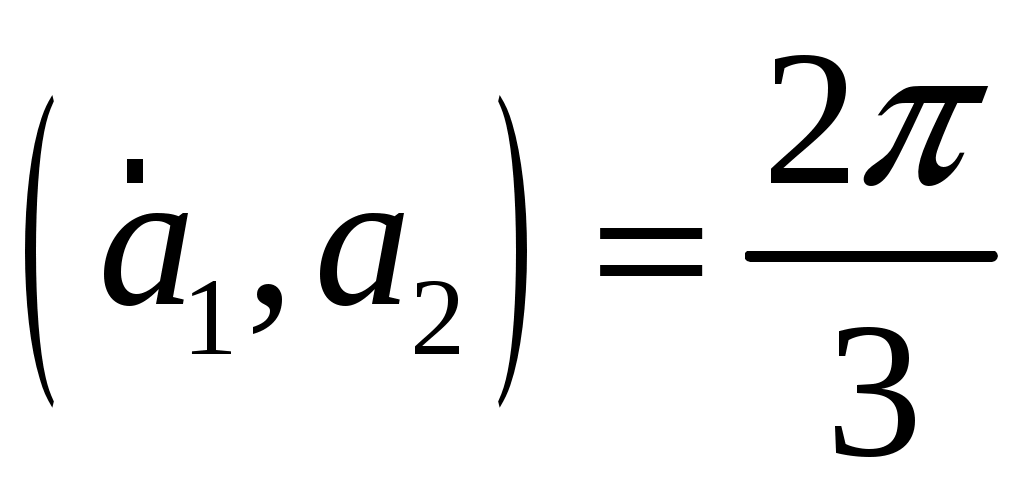 . Вычислить . Вычислить 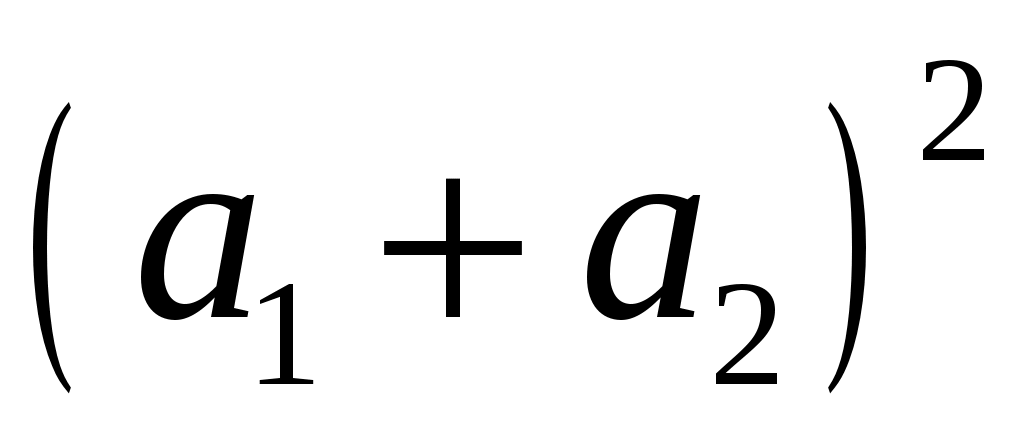 . .
|
13
|
12
|
1.66
|
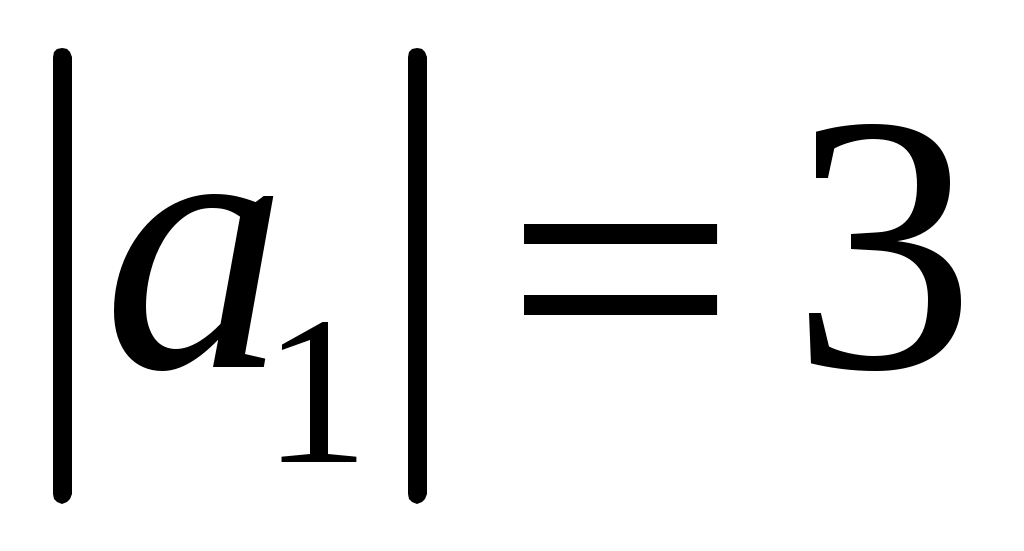 , , 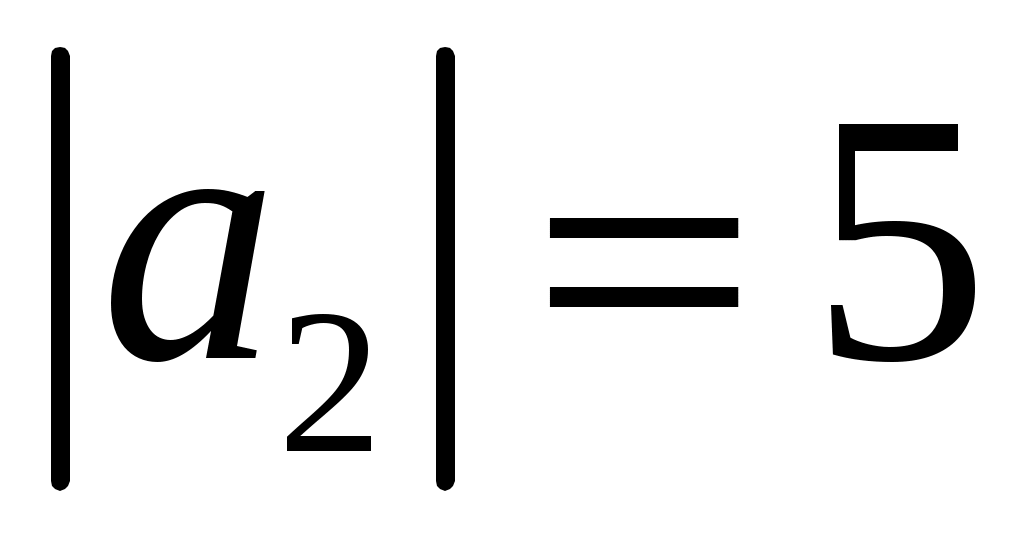 . Определить, при каком значении . Определить, при каком значении  векторы векторы 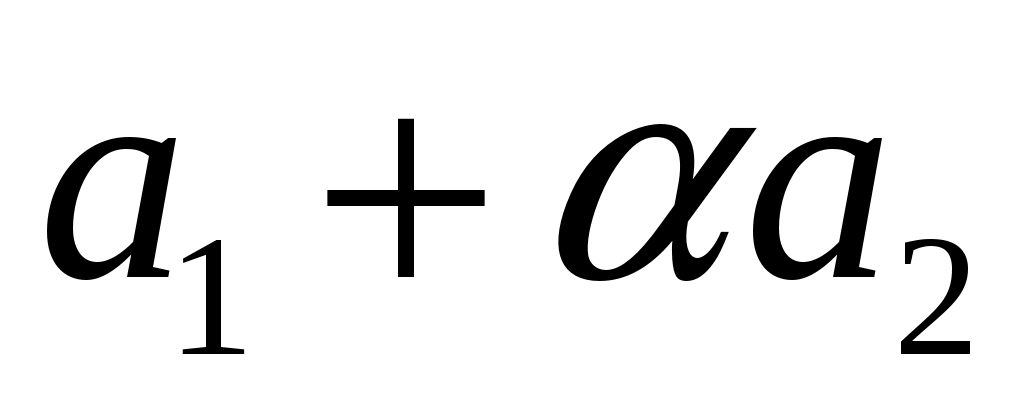 и и 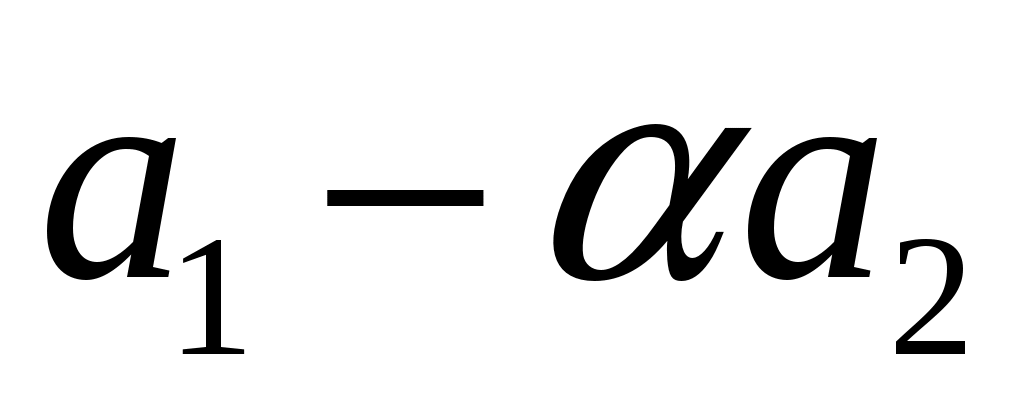 будут перпендикулярны. будут перпендикулярны.
|
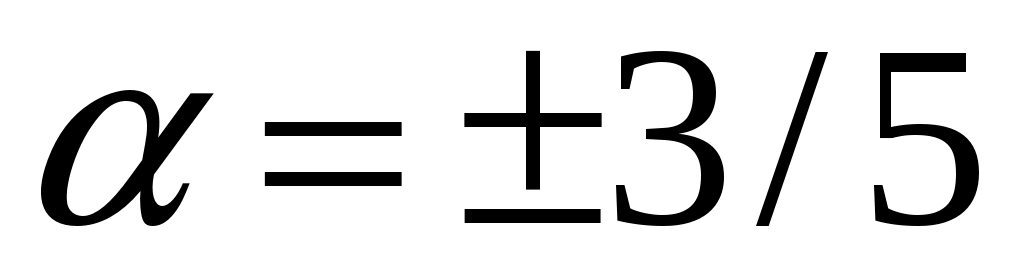
|
13
|
1.67
|
Вычислить длину диагоналей параллелограмма, построенного на векторах 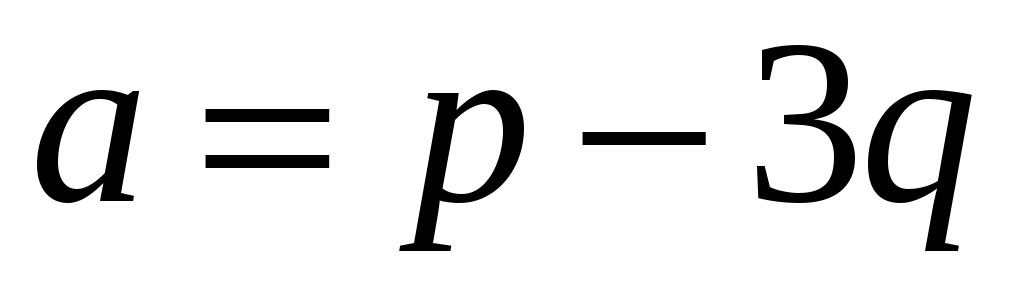 , , 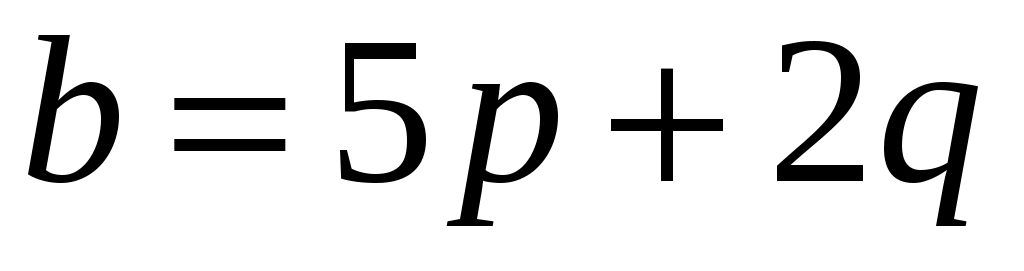 , если известно, что , если известно, что 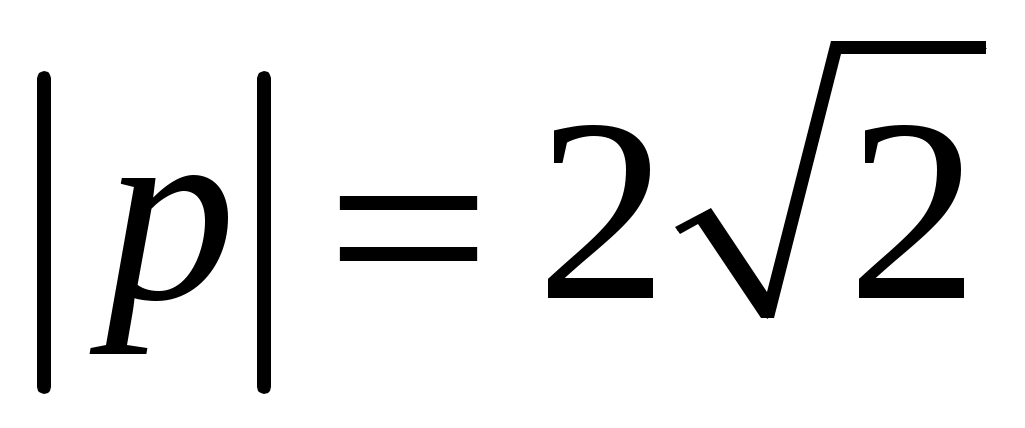 , , 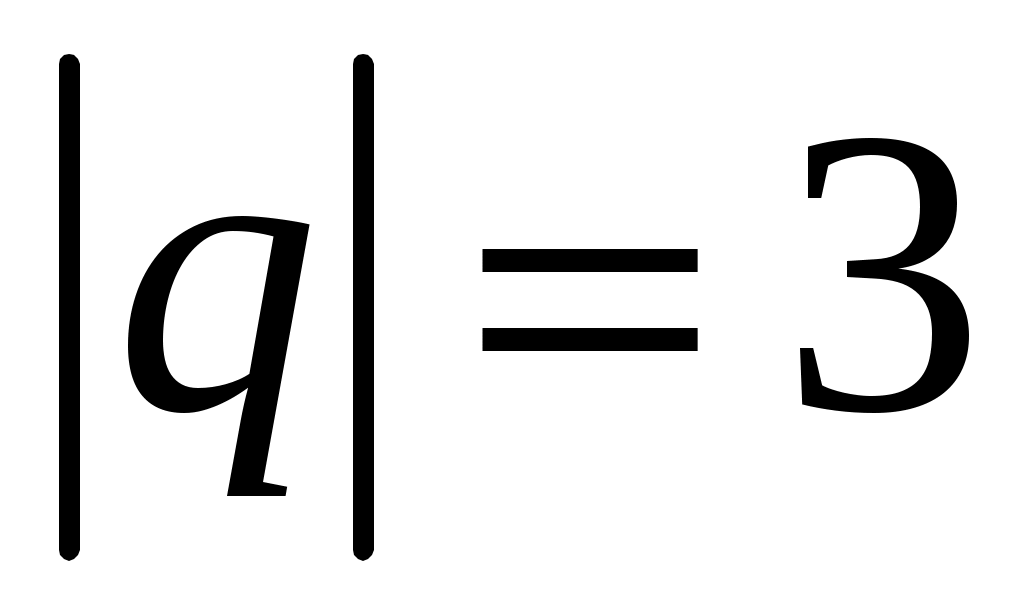 и и 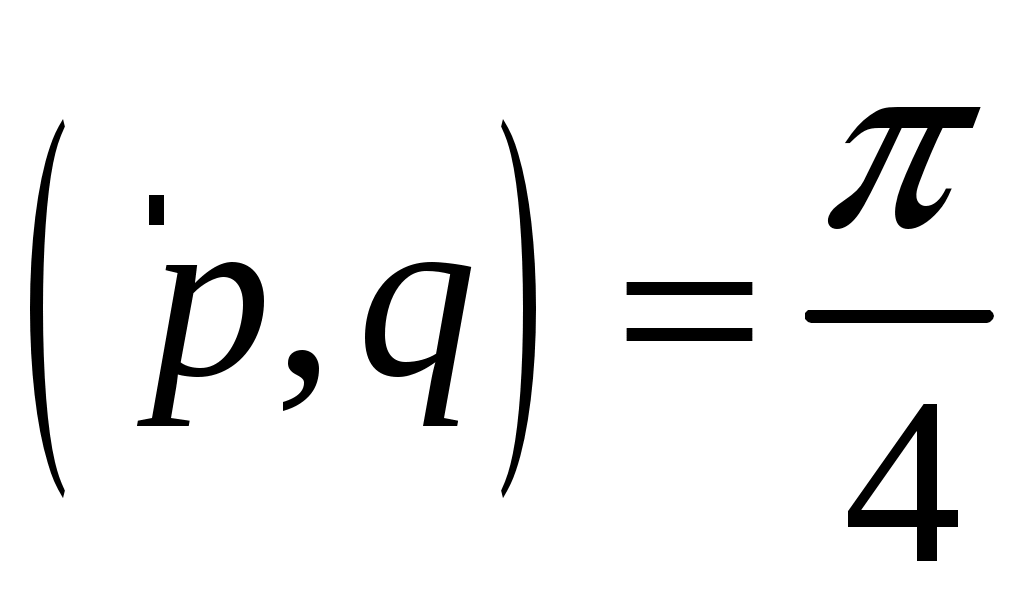 . .
|
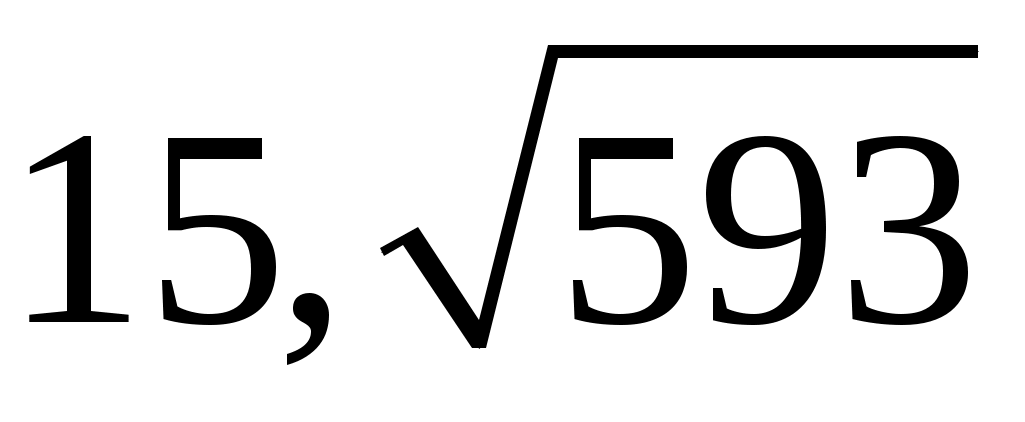
|
14
|
1.69
|
В треугольнике АВС 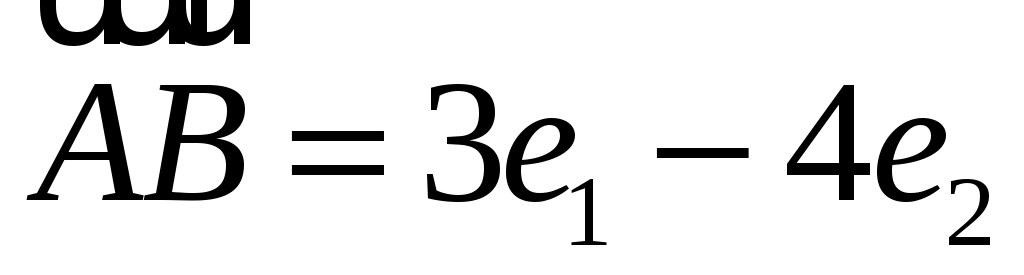 , , 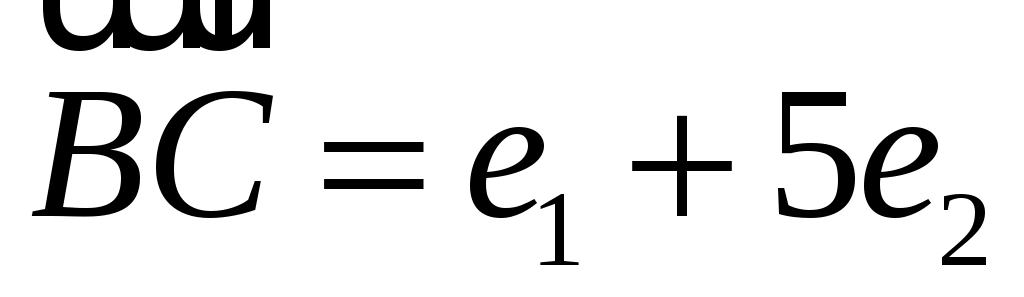 . Вычислить длину его высоты . Вычислить длину его высоты 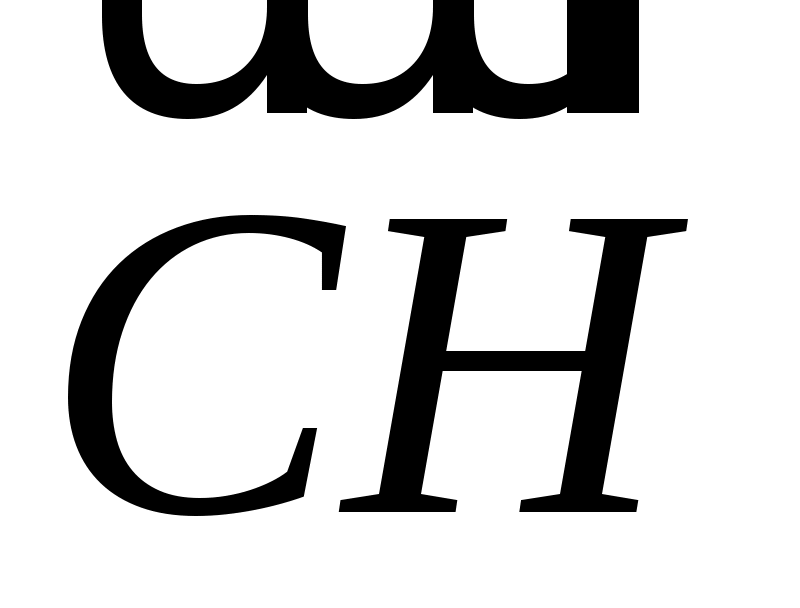 , если известно, что , если известно, что 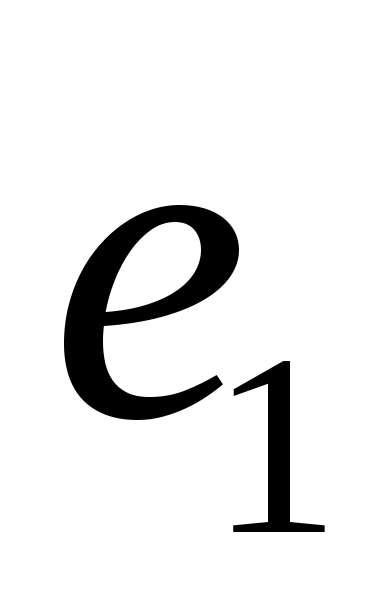 и и 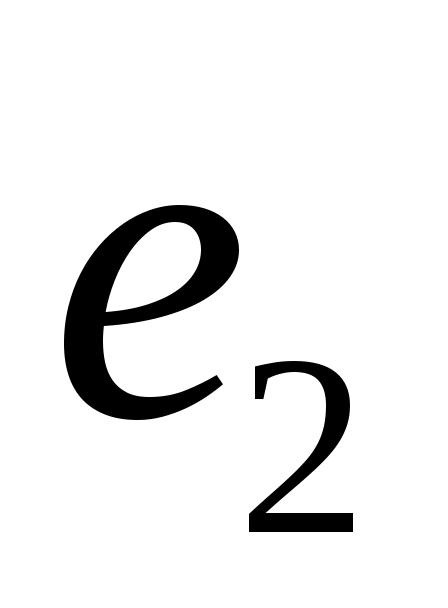 взаимно перпендикулярные орты. взаимно перпендикулярные орты.
|
19/5
|
15
|
1.72
|
Найти угол, образованный единичными векторами 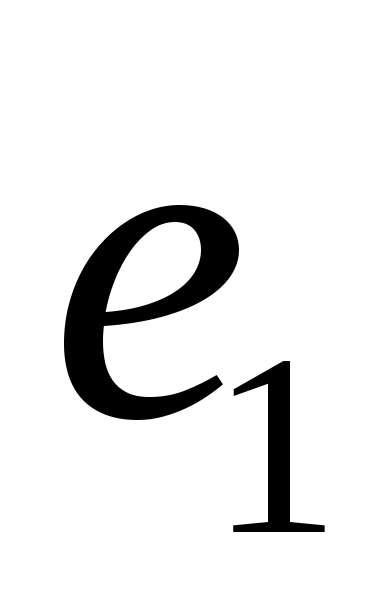 и и 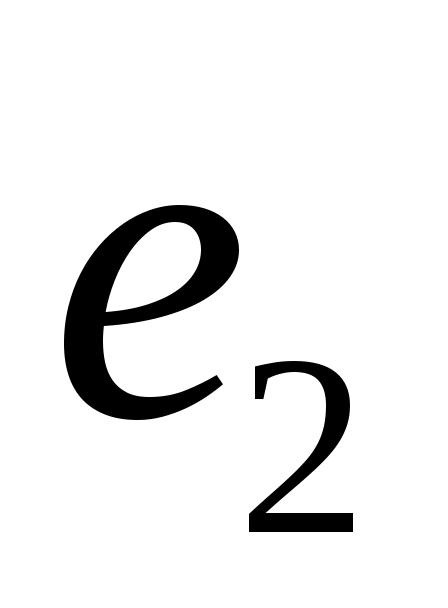 , если известно, что векторы , если известно, что векторы 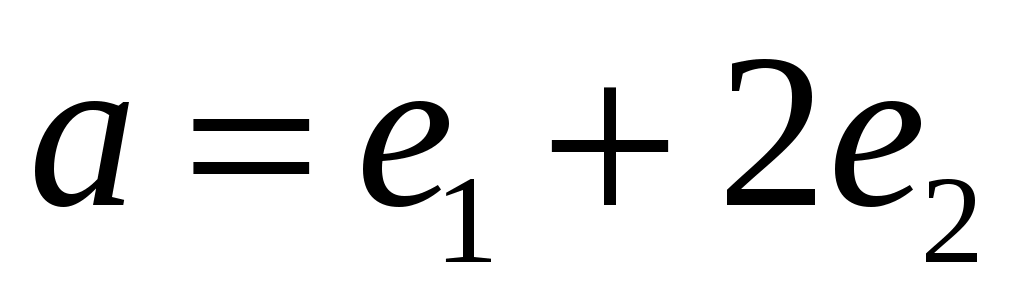 и и 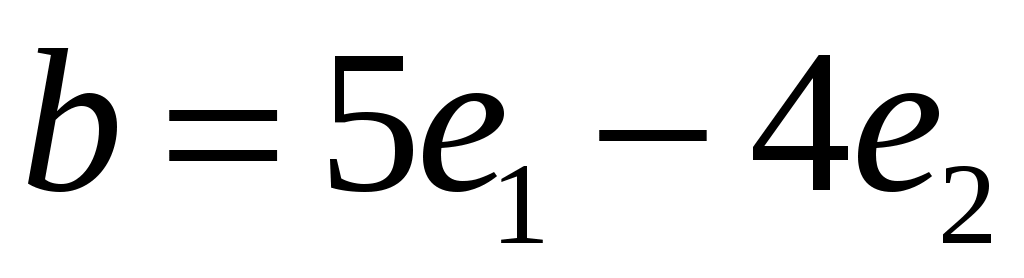 перпендикулярны. перпендикулярны.
|
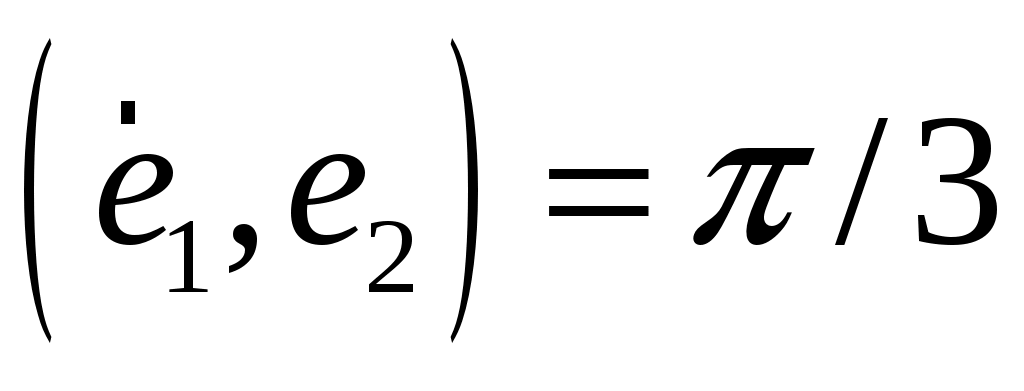
|
16
|
1.78 г, ж, з, и
|
Даны векторы 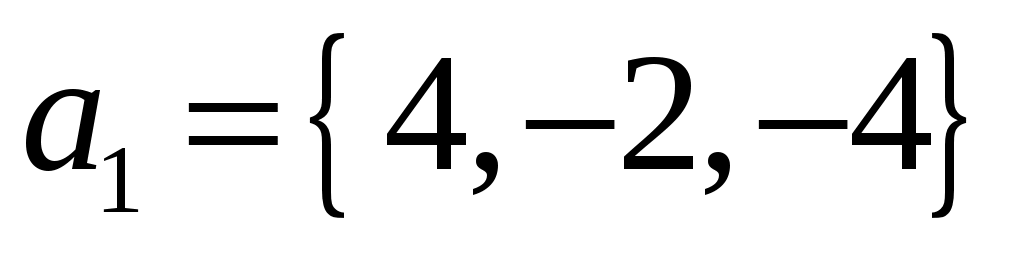 и и 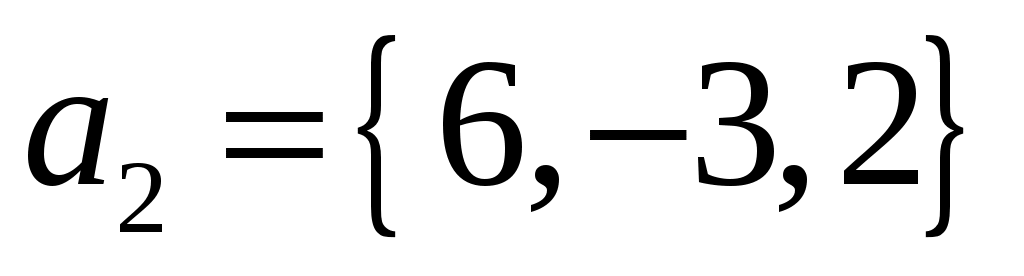 . Вычислить: г) . Вычислить: г) 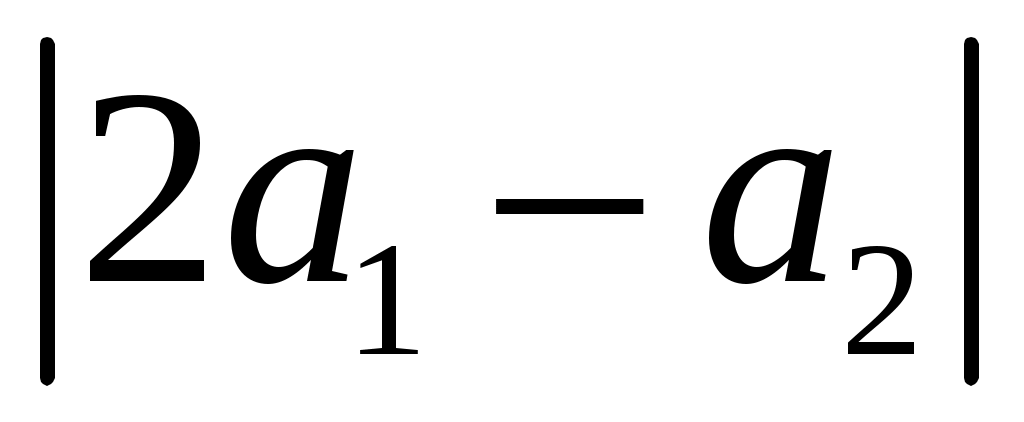 ; ж) направляющие косинусы вектора ; ж) направляющие косинусы вектора  ; ;
з) 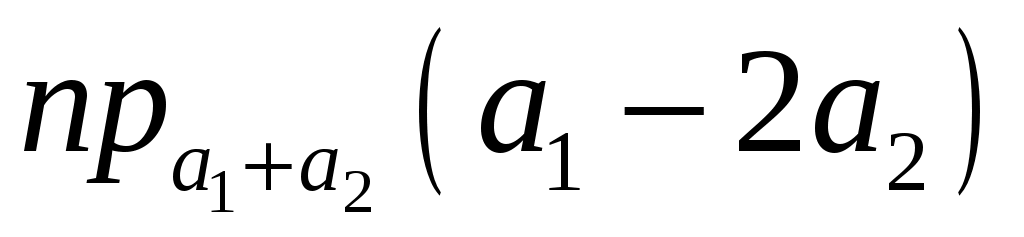 ; и) ; и) 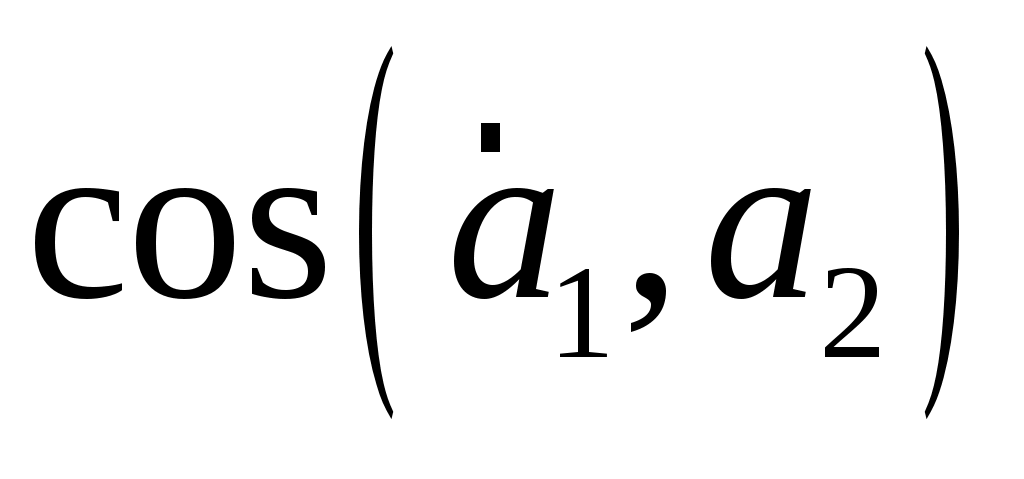 . .
|
г) 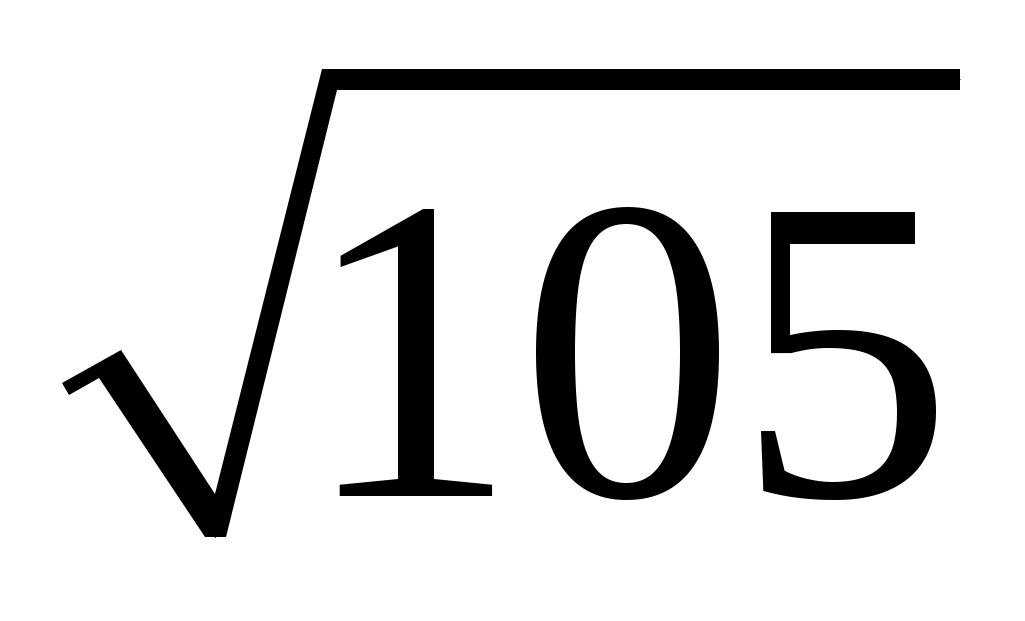 ; ;
ж) 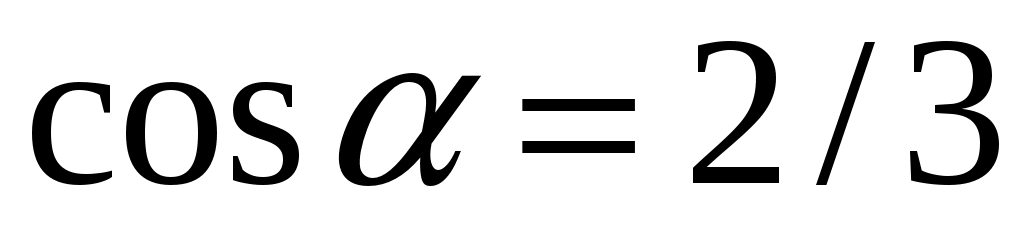 , , 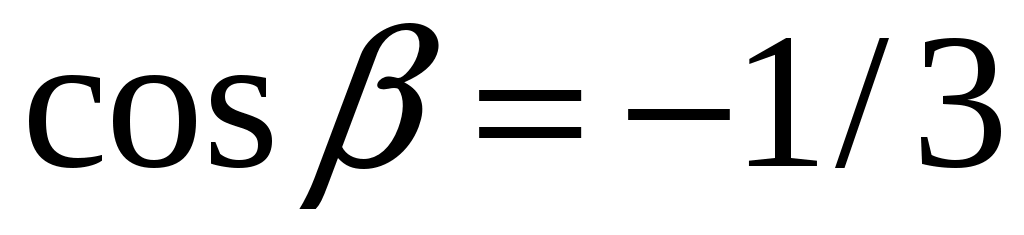 , , 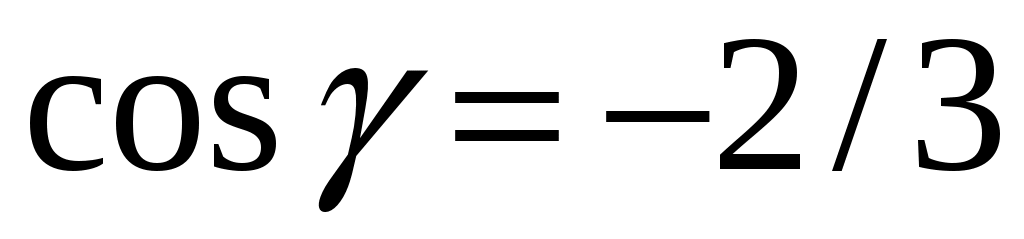 ; ;
з) 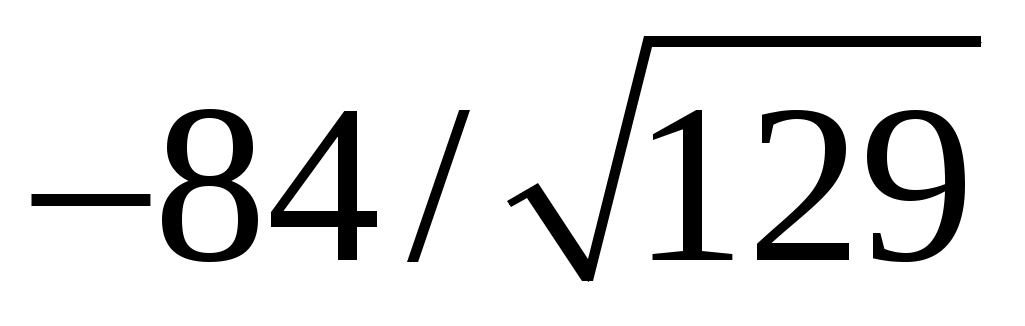 ; ;
и) 11/21.
|
|
 Скачать 320.5 Kb.
Скачать 320.5 Kb.