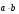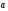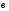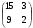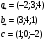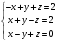|
|
ДЗ по теории вероятностей 2_очники. Дз по теории вероятностей 2 типовые билеты коллоквиуму 1 по математике. Домашнее задание по теории вероятностей
ДЗ по теории вероятностей 2 + типовые билеты коллоквиуму 1 по математике.
Домашнее задание по теории вероятностей.
Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях—четная, причем на грани хотя бы одной из костей появится шестерка.
При перевозке ящика, в котором содержались 21 стандартная я 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно на� званное двузначное число; б) случайно названное двузнач�ное число, цифры которого различны.
Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб»
В группе 18 студентов, среди которых 10 отличников. По списку наудачу отобраны 14 студентов. Найти вероятность того, что среди отобранных студентов 6 отличников.
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных И изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.
На стеллаже библиотеки в случайном порядке расставлено 25 учебников, причем пять из них красные. Студент берет наудачу 2 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется красным (событие А).
В ящике 8 деталей, из которых четыре окрашены, взяли наудачу три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,9, а для второго—0,95. Найти вероят�ность того, что при одном залпе в мишень попадает только один из стрелков.
Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,45. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,9.
В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библио�текарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
Среди 100 лотерейных билетов есть 8 выигрыш� ных. Найти вероятность того, что 4 наудачу выбранные билета окажутся выигрышными.
Студент знает 30 из 50 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
Студент 1 го курса Сергей влюбился в свою однокурсницу Настю и решил подергать ее за волосы. Проблема в том, что Маша носит дреды в количестве 69 штук и гриндерсы. И очень не любит, когда ее дергают за дреды. При этом достаточно дернуть всего за 3 различных дреда, чтобы Настя пнула того, кто это сделал. Определите, сколькими способами Сергей может дернуть Машу 3 раза, чтобы получить гриндерсами.
Типовой билет к коллоквиуму – на целую пару работы.
Пусть А ={0;7;6;5;8;11;14} В={ 3,5,2,11;8}. Найти АÈ В, АÇ(В È{Ø})
| - Даны векторы
 (7;1:-8) и (7;1:-8) и  (6;4;-3). Найти скалярное произведение (6;4;-3). Найти скалярное произведение 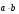 . . | Найти длину вектора  . . | - Определить площадь треугольника, построенного на векторах
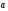 =(1;5;1), =(1;5;1), 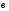 =(0;0;1). =(0;0;1). | Найти сумму А+В, если А=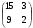 , В= , В= . . | Найти произведение АВ, если A= , B= , B= . .
| Вычислить определитель detA, если матрица A= | Вычислить объем параллелепипеда на векторах 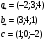 | Решить систему линейных уравнений: 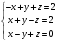
| Найти область определения функции   |
Вычислить предел
|
Вычислить производную функции 
|
Вычислить производную 
|
Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,28; 0,48: 0,62; 0,75.
|
15.Банк «Русский стандарт» проводит лотерею для своих клиентов —
держателей карт Visa Classic и Visa Gold. Будет разыграно 6 автомобилей
Jaguar, 2 автомобиля Bentley и 100 телефона iPhone . Известно,
что менеджер Александр оформил карту Visa Classic и стал победителем лотереи.
Какова вероятность, что он выиграет автомобиль Jaguar, если приз
выбирается наугад?
|
16.В холодильнике лежат 8 видов кошачьего корма в консервах, а на полке —
еще 3 вида сухого корма ( в том числе и Китикет). Ежедневный рацион кота состоит из 3 различных видов корма, причем коту безразлично, сухой это корм или в консервах. Сколько существует различных способов накормить кота, причем Китикет кот должен получать каждый день.
| |
|
|
 Скачать 43.44 Kb.
Скачать 43.44 Kb.