Содержание деятельностного подхода. Содержание деятельностного подхода в обучении решению олимпиадны. Е. И. Давыдова Рязанский государственный университет имени С. А. Есенина, Рязань, Российская Федерация

• Название: Е. И. Давыдова Рязанский государственный университет имени С. А. Есенина, Рязань, Российская Федерация
• Анкор: Содержание деятельностного подхода
• Дата: 01.04.2023
• Размер: 375.11 Kb.
• Имя файла: Содержание деятельностного подхода в обучении решению олимпиадны.docx
• Тип: Урок; #1030118

УДК 372.851

Е.И. Давыдова

Рязанский государственный университет имени С.А. Есенина,

Рязань, Российская Федерация

ОЦЕНКА ЭФФЕКТИВНОСТИ ДЕЯТЕЛЬНОСТНОГО ПОДХОДА В ОБУЧЕНИИ РЕШЕНИЮ ОЛИМПИАДНЫХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ

Аннотация. В статье рассматриваются особенности организации деятельностного подхода в обучении решению олимпиадных задач на уроках математики, приводятся примеры рассматриваемых задач, проводится оценка эффективности, выбранной методики.

Ключевые слова: олимпиадная задача, урок математики, деятельностный подход, деятельность ученика, задание, деятельность учителя.

E.I. Davydova

Ryazan State University named after S. A. Esenin,

Ryazan, Russian Federation

EVALUATION OF THE EFFECTIVENESS OF THE ACTIVITY APPROACH IN TEACHING THE SOLUTION OF OLYMPIAD PROBLEMS IN MATHEMATICS LESSONS

Annotation. The article discusses the features of the organization of the activity approach in teaching the solution of Olympiad problems in mathematics lessons, provides examples of the tasks under consideration, evaluates the effectiveness of the chosen methodology.

Keywords: Olympiad task, math lesson, activity approach, student activity, task, teacher activity.
Деятельностный подход в обучении определяется как процесс усвоения содержания обучения и развитие обучающегося в процессе его собственной активной деятельности.

Под деятельностью понимается процесс умственной активности обучающегося, характеризуемый предметом, потребностью и мотивом [1,стр. 54].

Предмет деятельности – это то, на что направлен процесс обучения [2, стр. 129].

Сущность деятельностного подхода в обучения выражается 3 положениями.

Способ действия является конечной целью обучения.

Способ действий может быть сформирован только в результате деятельности. Механизм обучения это не передача знаний, а управление учебной деятельностью.

Деятельностный подход представляет собой вззаимосвязь двух самостоятельных деятельностей обучающегося.

В деятельности учителя выделяется три центральных аспекта.

Планированние учебной деятельности.

Ее организация и проведение.

Контроль учебной деятельности.

Учебная деятельность это деятельность обучающегося.

Обучение и развитие обучающегося происходит только в процессе направленной деятельности на изучение и познание. Это положение составляет основу подхода к обучению деятельностного типа.

Под учебной деятельностью понимается приобретение как теоритических, так и практических знаний по данному предмету, формирование и развитие личности обучающегося[3, стр. 43].

Цель учебной деятельности формируется учителем и не известна до факта начала обучения.

Решение учебных задач это самое главное в обучении и составляет ядро обучения.

В учебной задаче главное значение имеет процесс его получения. Так как в процессе формируется знание, которое дает познание.

Учебная деятельность - желание помноженное на результат деятельности учащегося.

Управление учебной деятельностью нужно для того, чтобы цель и продукт учебной деятельности составляли единое целое.

Детская мотивация это самая сложная структура. Очень часто она отсутсвует. [4, стр.78].

Учебная деятельность – это сложная совокупность, каждый элемент которой занимает своё собственное место и имеет соответствующее оформление.

Реализация деятельностного подхода опосредована проблемными ситуациями, выступающими в роли учебно-познавательного мотива.

Проблемная ситуация создаётся для определения цели деятельности обучающихся и является своего рода учебной задачей, которую обучающиеся решают в процессе изучения новой темы. В то же время учебная задача требует обобщения теоретического материала и направлена на овладение обучающимися УУД.

Деятельностный подход отличается тем, что получение знаний и умений ведётся с помощью теоретического обобщения изучаемого материала, что способствует развитию критического мышления обучающихся. Деятельностный подход в обучении математике направлен на понимание и внедрение полученных знаний с помощью применения на уроках математики [4, стр. 87].

Среди учебных задач есть как общие, так и частые. Между ними есть строгие связи. Каждая система задач состоит из 1 основной и нескольких частных задач, направленных на понимание всего раздела. Решение этих задач ведет за собой понимание структуры и дает возможность овладеть всеми тонкостями приобретения новых знаний.

Рисунок 1 – Компоненты учебной деятельности
В деятельностном подходе к обучению основным является формирование у обучающихся приемов учебной деятельности.

Умственная и учебная деятельности дают точную дидактическую систему. Между этими системами приемов невозможно опредедить четкую границу.

В реализации системы приемов учебной деятельности предусмотрены последовательности их изучения в учебном материале.

Система приемов учебной деятельности включает в наблюдение, анализ, синтез, выделение свойств предметов, выделение основного сравнение, моделирование, классификация.

Первый этап это этап мотивации и целеполагания. Обучающиеся приступают к выполнению задач, актуализирующих их же знания. В список задач включен вопрос, создающий проблему, личностно значимую для ученика и формирующую у него потребность освоения того или иного понятия. Четко формулируется познавательная цель.

Второй этап это решение проблемы, которое осуществляется самими обучающимися в ходе диалога. Учитель организует эвристическую беседу. В завершение подводится итог.

Данный этап позволяет вовлечь обучающихся в активную работу, в которой нет равнодушных, Диалогическая фор­ма поиска решения проблемы является важнейшим компонентом деятельностного подхода.

Обучающихся подкрепляет свою письменную речь и озвучивает свою внутреннюю речь, тем самым осуществляется закрепление материала. От полноты и многократности проигрывания учебного материала в самостоятельных действиях обучающихся и зависит эффективность первичного закрепления.

Самоконтроль и рефлексия – крайний этап. Самоконтроль дает оценку своим действиям и дает ответственно относится к занятиям.

Процесс рефлексии не сопровождается громкой речью, а переходит во внутреннее планирование. На этом этапе для каждого обучающегося необходимо создать ситуацию успеха (я могу, у меня получается).

Перечисленные выше четыре этапа работы над понятием рекомендуется проводить всё на одном занятии.

На данном этапе происходит интеграция полученных ранее знаний с новым материалом, и опере­жающая подготовка обучающихся к следующим темам.

Следующий этап тренировочные упражнения. На этом этапе происходит отработка и закрепление изученного материала, выведение его на уровень автоматизированного умственного действия. Данный прием позволяет каждому обучающемуся двигаться вперед в собственном темпе: дети с невысоким уровнем подго­товки имеют достаточно времени, чтобы «не спеша» усвоить материал, а более подготовленные дети постоянно получают «пищу для размышлений».

Следующий этап контроль. При выполнении данного условия сводится на нуль негативная реакция обучающихся на отметки, эмоциональное давление ожидаемого результата в виде отметки. Задача учителя – вывести оценку усвоения учебного материала по планке, необходимой для дальнейшего продвижения.

Коллективный диалог это основная форма организации учебно-познавательной деятельности учеников в деятельностном подходе. Именно с его поомщью осуществляется общение учителя с учеником, в процессе которого усваивается учебный материал на уровне личностной адаптации. Диалог может существовать в любых микро-группах. Спектр форм урока может использоваться в рамках деятельстного подхода.

При решении задач полезными могут оказаться советы участнику олимпиады. Приводим их:

1. Прочитайте условия всех задач и составьте план, согласно которому вы будете их решать. Учитывайте, что обычно задачи упорядочены по возрастанию их трудности.

2. Если условие, на ваш взгляд, можно понять разными способами, то обращайтесь к дежурному с вопросом.

3. Если задача решилась слишком легко – это подозрительно, возможно, вы неправильно поняли условие или где-то ошиблись.

4. Если задача не решается – попробуйте её упростить (взять меньшие числа, рассмотреть частные случаи и т.д.) или порешать ее «от противного», или заменить числа буквами и т.д.

5. Если неясно, верно ли некоторое утверждение, то пытайтесь его поочередно то доказывать, то опровергать.

6. Не зацикливайтесь на одной задаче: иногда отрывайтесь от нее и оценивайте положение. Если есть небольшие успехи, то продолжайте трудиться и мыслить, не останавливайтесь! Если размышления зашли в тупик, то задачу лучше отложить на некоторое время.

7. Если устали, отвлекитесь на несколько минут (посмотрите на облака или просто отдохните).

8. Решив задачу, сразу оформляйте решение. Это поможет проверить его правильность и освободит внимание для других задач.

9. Каждый шаг решения надо формулировать, даже если он кажется очевидным. Удобно записывать решение в виде нескольких утверждений (лемм). Это помогает при проверке и обсуждении работы.

10. Перед тем как сдать работу, перечитайте её «глазами проверяющих» – смогут ли они в ней разобраться?

Под олимпиадой понимается соревнование обучающихся на лучшее выполнение определенных заданий в какой-либо области знаний, в частности в математике.

В ходе исследования были разработаны дидактические материалы для подготовки обучающихся 7 классов к школьному и муниципальному этапу олимпиады, а также задания, способствующие развитию творческого, критического и логического видов мышления.

Содержание дидактических материалов:

• 
  Основные методы решения нестандартных задач.
  
• 
  Типология нестандартных задач для подготовки в математическим олимпиадам.
  
• 
  Арифметические задачи.
  
• 
  Алгебраические задачи.
  
• 
  Геометрические задачи
  
• 
  Задачи на специальные методы решения.
  
• 
  Задачи на разные методы решения.
  

Целью экспериментальной работы с обучающимися является доказательство эффективности применения деятельностного подхода к обучению решению олимпиадных задач.

Для достижения поставленной цели исследования был проведен педагогический эксперимент на базе гимназии № 2 г. Рязани в течении 2021-2022 учебного года. Участниками педагогического эксперимента стали обучающиеся 7 «Б» и 7 «В» классов.

С обучающимися экспериментальной и контрольной групп было проведено входное тестирование, а также тестирование уровня мотивации, интеллектуальной лабильности, наблюдательности. В течение учебного года на уроках и внеурочных занятиях обучающиеся экспериментальной группы решали олимпиадные задачи.

По данным исследования мотивации до проведения эксперимента был выявлен достаточно невысокий уровень в контрольной и экспериментальной группах.

Повторное тестирование показало положительную динамику мотивации обучающихся экспериментальной группы. Результаты контрольного этапа исследования показали, что у большинства обучающихся выросли значения познавательной мотивации.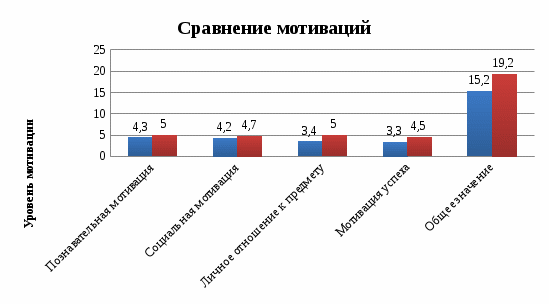

Рисунок 2. Сравнение мотиваций обучающихся.

При изучении уровня наблюдательности так же заметна положительная динамика. Процент детей с высокой наблюдательностью повысился с 25% до 28%, при этом количество учащихся с низкой наблюдательность сократилось с 11% до 4% .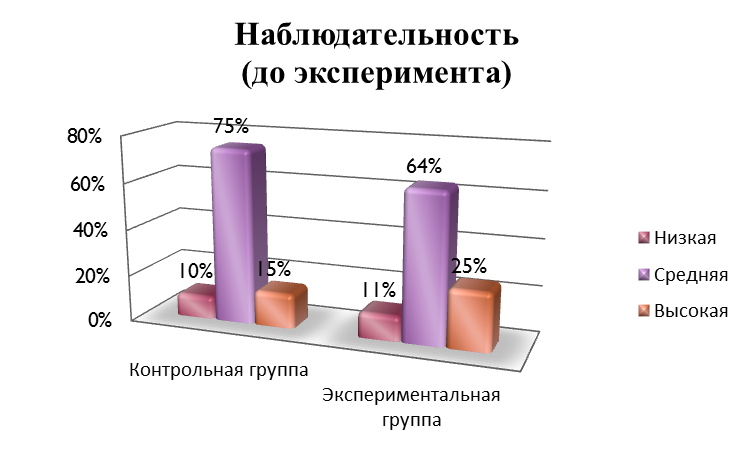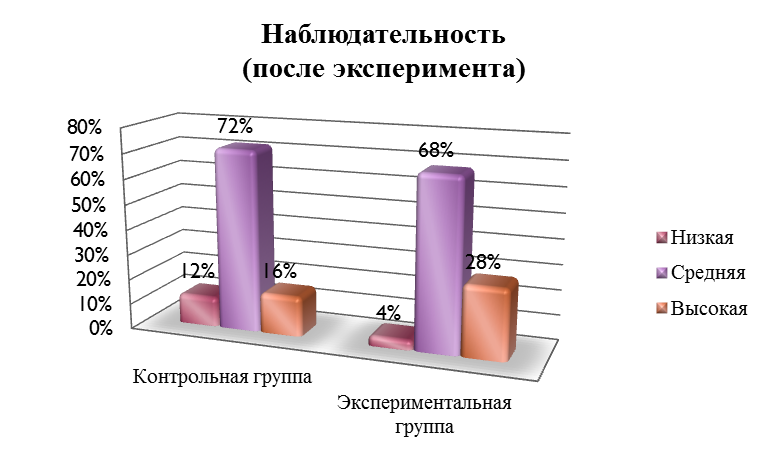

Рисунок 3. Динамика наблюдательности обучающихся.

При повторной проверке скорости мышления наблюдается значительное увеличение учащихся с высокой скоростью мышления с 18% до 24%, при этом процент учащихся с низкой скоростью мышления уменьшился с 46% до 36%.

Полученные результаты, позволяют видеть рост количества, решенных задач у обучающихся экспериментальной группы после окончания эксперимента.

Показатель среднего числа правильно решенных задач также вырос в обеих группах. В контрольной группе он увеличился с 7,35 до 7,65. В экспериментальной более заметно – с 7,21 до 8,92.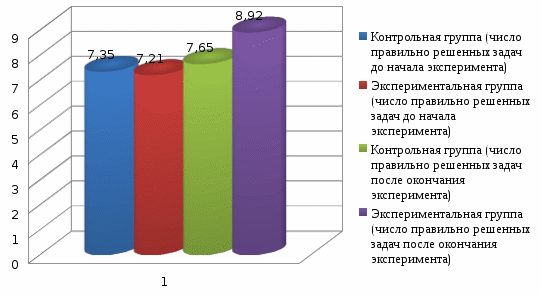


Рисунок 4. Динамика среднего числа правильно решённых задач.

На рисунке наглядно видно различие, что можно объяснить влиянием исследуемой педагогической методики.

После проведения эксперимента значение критерия Крамера-Уэлча больше критической величины (1,96), следовательно, достоверность различий характеристик контрольной и экспериментальной групп составляет 95 %.

Таким образом, начальные состояния экспериментальной и контрольной групп совпадают, а конечные – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения.

Результаты проведенной методико-экспериментальной работы позволяют сделать вывод о том, что предлагаемая методика деятельностного подхода в обучении решению олимпиадных задач способствует развитию экспериментальных умений и творческих способностей обучающихся, увеличивает познавательный интерес к предмету, повышает уровень активности обучающихся на уроке.

В ходе эксперимента было выявлено:

повышение эффективности учебного процесса, благодаря решению олимпиадных задач с применением деятельностного подхода;

значительное улучшение качества знаний и познавательной активности обучающихся;

увеличился уровень мотивации обучающихся.
Библиографический список

1. 
   Андронов И.К. Полвека развития школьного математического образования в СССР.– М.: Просвещение, 1967.
   
2. 
   Беспалько В.П. Слагаемые педагогической технологии. – М.: Педагогика, 1989.
   
3. 
   Виноградова Л.В. Методика преподавания математики в средней школе (общая методика): Учебное пособие.- Петрозаводск, 2003.
   
4. 
   Байдак В.А., Борисова Л.П. Формирование приемов учебной деятельности в обучении математике в школе. // Модернизация педагогического образования в Сибири: проблемы и перспективы. Сборник научных статей. Омск: Изд-во ОмГПУ, 2002. С. 184-189.
   
5. 
   Голубев В.И. Решение сложных и нестандартных задач по математике. М. 2017. 321с.
   
6. 
   Епишева О.Б. Технология обучения математике на основе деятельностного подхода: Кн. Для учителя.- М.: Просвещение, 2013. 223 с.
   
7. 
   Рудник А.В. Переформулирование текста задачи как путь отыскания ее решения // Из опыта преподавания математики в школе: Пособие для учителей. М.: Просвещение, 2018. С. 119-128.