профиль. Егэ по математике 27. 03. 2023. Досрочная волна. Москва Тип 1 639637
 Скачать 118.91 Kb.
|
|
ЕГЭ по математике 27.03.2023. Досрочная волна. Москва 1. Тип 1 № 639637 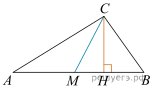  Острый угол В прямоугольного треугольника равен 66°. Найдите угол между высотой СН и медианой СМ, проведенными из вершины прямого угла. Ответ дайте в градусах. 2. Тип 2 № 639638 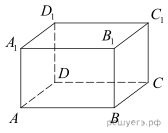 Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда  у которого    3. Тип 3 № 639639 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. 4. Тип 4 № 639640 В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах. 5. Тип 5 № 639641 Найдите корень уравнения  6. Тип 6 № 639642 Найдите значение выражения  7. Тип 7 № 639643 На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10]. 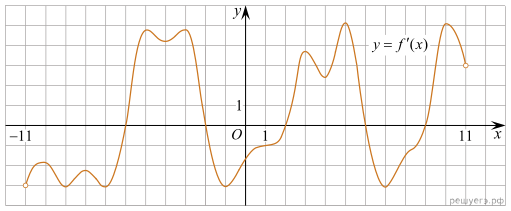 8. Тип 8 № 639644 Водолазный колокол, содержащий в начальный момент времени  моль воздуха объeмом  л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма  Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где  − постоянная, а  − температура воздуха. Какой объeм  (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10 350 Дж?9. Тип 9 № 639645 Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе? 10. Тип 10 № 639646 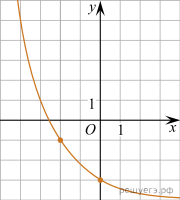 На рисунке изображен график функции вида  Найдите значение f (−8).11. Тип 11 № 639647 Найдите точку минимума функции  12. Тип 12 № 639648 а) Решите уравнение:  б) Укажите корни этого уравнения, принадлежащие отрезку  13. Тип 13 № 639649 Дан тетраэдр ABCD. Точки K, L, M, N лежат на ребрах AC, AD, DB и BC соответственно, так, что четырехугольник KLMN квадрат со стороной 2, AK : KC = 2 : 3. а) Докажите, что  б) Найдите расстояние от точки C до плоскости KLМN, если известно, что объем тетраэдра ABCD равен 25. 14. Тип 14 № 639650 Решите неравенство  15. Тип 15 № 639651 В июле 2023 года планируется взять кредит на некоторую сумму. Условия возврата таковы: — каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга. Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 65 500 рублей больше суммы, взятой в кредит? 16. Тип 16 № 639652 Точка В лежит на отрезке АС. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром АВ в точке K. Продолжение отрезка МВ пересекает окружность с диаметром AB в точке D. а) Докажите, что прямые AD и МC параллельны. б) Найдите площадь треугольника DBC, если AK = 5 и KM = 25. 17. Тип 17 № 639653 Найдите все значения a, при каждом из которых уравнение  имеет ровно один корень. 18. Тип 18 № 639654 Дано натуральное число. К этому числу можно либо прибавить утроенную сумму его цифр, либо вычесть утроенную сумму его цифр. После прибавления или вычитания суммы цифр, число должно остаться натуральным. а) Можно ли получить из числа 128 число 29? б) Можно ли получить из числа 128 число 31? в) Какое наименьшее число можно было получить из числа 128? |