Методы экстраполяции. Экономические науки Каждый из них имеет свои

• Название: Экономические науки Каждый из них имеет свои
• Анкор: Методы экстраполяции
• Дата: 22.12.2022
• Размер: 33.07 Kb.
• Имя файла: metody-prognoznoy-ekstrapolyatsii-v-tehnicheskom-servise.docx
• Тип: Документы; #859828

Экономические науки

Каждый из них имеет свои плюсы и минусы. Скорость поможет быстро реанимировать фирму в кризисной ситуации, поставить ее на ноги, но качест- во покажет, что успех достигается медленнее, но держится дольше. Таким образом, если говорить о политике грамотного руководителя бизнес проектов, то, несомненно, стоит отдать предпочтение качественной реорганизации.

Но стоит рационально оценивать свои силы, так как качественные из- менения требуют гораздо больше материально затратных вложений, боль- ших инвестиций, соответственно это несет в себе большие риски. Никто ни- когда не сможет дать гарантий, что ваше предприятие не обанкротится, ни один эксперт, каким бы высококвалифицированным он ни был, не подпи- шется под этим утверждением. Поэтому при реорганизации своего бизнеса стоит продумывать политику действий на несколько шагов вперед, начиная с выхода из кризисной ситуации и заканчивая стратегией развития предпри- ятия на несколько лет вперед.

В современном мире появилось такое понятие как «бизнес-технология», это как раз и есть та самая стратегия развития. И от выбора верной техноло- гии и зависит успешность и рентабельность вашего предприятия. Посколь- ку понятие включает в себя все основные постулаты грамотно организован- ной фирмы.

Тем самым, можно сказать, что современный мир функционирует по принципу естественного отбора, выживает сильнейший. И чтобы оказаться в ряду «сильных» нужно принимать грамотные управленческие решения и разрабатывать стратегию, рассчитанную в первую очередь на развитие, на динамику, а не на стабильность и стагнацию.

Список литературы:

1. 
   Малый бизнес / Под ред. В.Я. Горфинкеля, В.А. Швандара. – М.: Юни- ти-Дана, 2006. – 496 с.
   
2. 
   Малое предпринимательство в России. Формирование нового сци- ального института / И.В.Долгорукова. – М.: Научная книга, 2010. – 156 с.
   
3. 
   Уемов А.И. Системный подход и общая теория систем / А.И. Уемов. – М., 2008. – 324 с.
   

МЕТОДЫ ПРОГНОЗНОЙ ЭКСТРАПОЛЯЦИИ В ТЕХНИЧЕСКОМ СЕРВИСЕ

© Котова Т.Н.^, Хачатурян Р.Е.

Технологический институт сервиса (филиал)

Донского государственного технического университета, г. Ставрополь

В научно-техническом и экономическом прогнозировании широкое применение получило математическое моделирование, базирующееся




^ Доцент кафедры «Общеобразовательные дисциплины», кандидат экономических наук.

на методах экстраполяции и статистическом анализе. В экстраполяци- онных прогнозах особо важным является не столько предсказание кон- кретных значений изучаемого объекта или параметра в определѐнном году, сколько своевременное фиксирование объективно намечающихся сдвигов, лежащих в основе назревающих тенденций.

Ключевые слова: моделирование, методы прогнозирования, методы экстраполяции, однофакторные функции.
Методы экстраполяции являются одними из распространенных и наи- более разработанных среди всей совокупности методов прогнозирования. При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения количественных характеристик объекта.

Следует обратить внимание на то, что сложные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при ста- тистическом анализе тенденций и экстраполировании, которое состоит в следующем:

• 
  во-первых, должно быть четкое определение задачи, выдвижение гипотез о возможном развитии прогнозируемого объекта, обсужде- ние факторов, стимулирующих и препятствующих развитию дан- ного объекта, определение необходимой экстраполяции и еѐ допус- тимой дальности;
  
• 
  во-вторых, выбор системы параметров, унификация различных еди- ниц измерения, относящихся к каждому параметру в отдельности;
  
• 
  в-третьих, сбор и систематизация данных. Перед сведением их в со- ответствующие таблицы еще раз проверяется однородность данных и их сопоставимость: одни данные относятся к серийным изделиям, а другие могут характеризовать лишь конструируемые объекты;
  
• 
  в-четвертых, когда вышеперечисленные требования выполнены, за- дача состоит в том, чтобы в ходе статистического анализа и непо- средственной экстраполяции данных выявить тенденции или сим- птомы изменения изучаемых величин.
  

Для повышения точности экстраполяции используются различные при- емы. Один из них состоит, например, в том, чтобы экстраполируемую часть тренда корректировать с учетом реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируе- мый объект.

При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого временного ряда, на которую уже наклады- ваются другие составляющие. Результат при этом связывается исключи- тельно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов.

Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исхо- дит из прошлого и настоящего, и тем самым накапливается погрешность. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпирическим зна- чениям применяется метод наименьших квадратов. Его сущность состоит в минимизации суммы квадратов отклонений между наблюдаемыми (факти- ческими) величинами и соответствующими оценками (расчетными величи- нами), вычисленными по подобранному уравнению связи.

Этот метод лучше других соответствует идее усреднения как единично- го влияния учтенных факторов, так и общего влияния неучтенных.

Рассмотрим простейшие приемы экстраполяции, применяя однофак- торные прогнозирующие функции.

Операцию экстраполяции в общем виде можно представить в виде оп- ределения значения функции:

Y
ˆ

tl

 f ( y

t ,l ⁾
(1)

tl
где Y^ˆ – экстраполируемое значение уровня;

t + l – период упреждения;

Y_t– уровень, принятый за базу экстраполяции.

Под периодом упреждения при прогнозировании понимается отрезок времени от момента, для которого имеются последние статистические дан- ные об изучаемом объекте, до момента, к которому относится прогноз.

Экстраполяция на основе среднего значения временного ряда.

В самом простом случае при предположении о том, что средний уро- вень ряда не имеет тенденции к изменению или если это изменение незна-

t l
чительно, можно принять Y^ˆ


 Y т.е. прогнозируемый уровень равен сред-

нему значению уровней в прошлом.

Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:

y^ˆ_tl Y t_aS_y

(2)

где t_a– табличное значение t-статистики Стьюдента с n – 1 степенями и уровнем вероятности p;

S _y – средняя квадратическая ошибка средней величины.

В свою очередь, среднее квадратическое отклонение для выборки равно: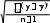

_S (3)
где y_t– фактические значения показателя.

Доверительный интервал, полученный как t_a, учитывает неопределен- ность, которая связана с оценкой средней величины.

Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием индивидуальных значений вокруг средней, составит

величину

^{s  s2} . Таким образом, доверительные интервалы для прогно-

2 _n

стической оценки равны:


Y
ˆ

t l




 Y  t_a S


(4)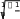

Экстраполяция по скользящей и экспоненциальной средней.

Для краткосрочного прогнозирования наряду с другими приемами мо- гут быть применены адаптивная или экспоненциальная скользящие сред-

ние. Если прогнозирование ведется на один шаг вперед, то

ˆ


Y
t l

 M_t ^или

Y
ˆ

t l

 N_t ^{, где Mt – адаптивная скользящая средняя; Nt – экспоненциальная}

средняя. Здесь доверительный интервал для скользящей средней можно оп- ределить по формуле (4), в которой число наблюдений обозначено символом

n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m, равным нечетным числам.

При экспоненциальном сглаживании, дисперсия экспоненциальной

средней равна <sup>

 S 2</sup> , где S – среднее квадратическое отклонение, а

2  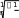

вместо величины в формуле (4) при исчислении доверительного ин-

тервала прогноза следует взять величину

или

. Здесь α –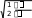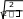

коэффициент экспоненциального сглаживания, изменяется от 0 до 1. Если 0 < α < 0,5, то при расчете прогноза учитываются прошлые значения вре- менного ряда, а при 0,5 < α < 1 – значения, близкие к периоду упреждения. Примерное значение коэффициента сглаживания определяют по формуле Р. Брауна:

  ²

m  1
(5)

где m – число уровней временного ряда, входящих в интервал сглажи- вания.

Экстраполяция на основе среднего темпа.

Если в основу прогностического расчета положен средний темп роста, то экстраполируемое значение уровня можно получить с помощью форму-

лы: Y  Y T ² , где T_p– средний темп роста, Y_t– уровень, принятый за ба-

tl t p

зу для экстраполяции.

Здесь принят только один путь развития – развитие по геометрической прогрессии, или по экспонентной кривой. Во многих же случаях фактиче- ское развитие явления следует иному закону, и экстраполяция по среднему темпу нарушает основное допущение, принимаемое при экстраполяции, – допущение о том, что развитие будет следовать основной тенденции – трен- ду, наблюдавшемуся в прошлом. Чем больше фактический тренд отличается от экспоненты, тем больше данные, получаемые при экстраполяции тренда, будут отличаться от экстраполяции на основе среднего темпа. Средний темп определяется на основе изучения прошлого, или оценивается каким-либо другим путем (например, подбор вариантов для различных ситуаций). В качестве исходного (базового) уровня для экстраполяции представляется естественным взять последний уровень ряда, поскольку будущее развитие начинается именно с этого уровня.

Статистическая надежность вышеприведенных методов оценивается с помощью коэффициента вариации:

V  ^100%

y

где – среднее квадратическое отклонение;


^y – среднее значение временного ряда.
(6)

Метод считается статистически надежным и может быть использован для прогнозирования, если значение коэффициента вариации не превышает 10 %.

В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а дей- ствие многочисленных влияющих на него факторов. Однако каждому момен- ту времени соответствуют определенные характеристики всех этих фактори- альных признаков, которые со временем в той или иной мере изменяются, т.е.

время можно рассматривать как интегральный показатель суммарного воз- действия всех факториальных признаков.

В качестве фактора-аргумента в однофакторной прогнозирующей функ- ции можно использовать не только время, но и другие факторы, если известна их количественная оценка на перспективу.

Наиболее простым из методов прогнозирования является экстраполяция тренда явления (процесса) за истекший период. Тренд (или вековая тенден- ция) характеризует процесс изменения показателя за длительное время, ис- ключая случайные колебания. Тренд явления находят путем аппроксимации фактических уровней временного ряда на основе выбранной функции. Наи- более часто применяемые при прогнозировании функции показаны в табл. 1.

Таблица 1

Однофакторные прогнозирующие функции

Наименования функции	Вид функции
Степенной полином	y a at at2  ...  atn 0 1 2 n
Парабола	y  a  a t  a t2 0 1 2
Линейная функция	y  a0  a1t
Экспоненциальная (показательная)	2 y ea0 a1ta2t, y ea0 a1t
Степенная	y  a0t 1 a
Логарифмическая	y  a0  a1 ln t
Комбинация линейной и логарифмической функций	y  a0  a1t  a2 ln t
Функция Конюса	y  t(a0  a1 ln t)
Функция Торнквиста	y  a0t a1  t
Логистическая (сигмоидальная)	y a0 1  aea2t 1
Частный случай логистической функции	y1 a  a et 0 1
Гипербола	y  a  a1 , y  a  a1 0 t 0 tn
Комбинация линейной функции и гиперболы	y  a  a t  a2 0 1 t

В них фактор-аргумент обозначен символом t. При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье. Степенной полином может описать любые процессы изменения показателя y в зависимости от значений t. Корреляционное от- ношение для степенного полинома, служащее мерой тесноты корреляцион- ной связи в нелинейных моделях, приближается к единице по мере увели- чения числа степеней полинома до числа уровней временного ряда.

Одновременно линия регрессии приближается к фактическим уровням по- казателя за прошедшее время, что не позволяет установить его тренд и экстра- полировать его на перспективу. Поэтому для прогнозирования обычно не при- меняют полином выше третьей степени. Таким образом, в качестве прогнози- рующей функции целесообразно использовать лишь три частных случая сте- пенного полинома: линейную модель, параболу и полином третьего порядка.

Линейная модель отражает постоянный ежегодный абсолютный при- рост в размере a₁, т.е. арифметическую прогрессию. Парабола описывает случаи увеличения абсолютного ежегодного прироста на постоянную вели- чину 2a₂, а третьего порядка – S-образную кривую с двумя точками изгибов. Показательная функция предусматривает постоянный ежегодный темп

роста, равный 100e^a1 процентов (т.е. геометрическую прогрессию), а второ-

го порядка – постоянное увеличение ежегодных темпов роста в ^ea2

раз. Сте-

пенная функция соответствует случаю ускоряющегося при a₁ > 1 или замед- ляющегося при a₁ < 1 роста абсолютного ежегодного прироста. Логарифми- ческая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая кривая представляет собой модифицированную геометриче- скую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу. Гиперболы характерны для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает.

Коэффициенты в однофакторных прогнозирующих функциях a₀ и a₁ определяются с помощью метода наименьших квадратов, сущность которо- го заключается в минимизации суммы квадратов отклонений фактических значений от расчетных:

t t
_( y  y^ˆ )²  min

t
где y^ˆ_t– вид исследуемой функции.
(7)

С помощью этих методов экстраполируются количественные парамет- ры больших систем, количественные характеристики экономического, науч- ного, производственного потенциала, данные о результативности научно- технического прогресса, характеристики соотношения отдельных подсис- тем, блоков, элементов в системе показателей сложных систем.

Список литературы:

1. 
   Афанасьев В.Н. Юзбашев М. М. Анализ временных рядов и прогно- зирование. – М.: «Финансы и статистика», 2012. – 320 с.
   

2. 
   Минько А.Э., Минько Э.В. под ред. А.С. Будагова. Методы прогнози- рования и исследования операций: учебное пособие. – М.: «Финансы и ста- тистика», 2010. – 480 с.
   
3. 
   Сторожук О.А. Моделирование и вариантное прогнозирование разви- тия техники. – М: «Машиностроение», 2005. – 252 с.
   

ПРОГНОЗИРОВАНИЕ РАЗВИТИЯ КУЛЬТУРЫ ПО САМАРСКОЙ ОБЛАСТИ

© Уткина Т.С.^

Самарский государственный университет, г. Самара

В ходе работы были рассмотрены основные задачи прогнозирования культуры. Проведен анализ статистических данных по библиотекам Самарской области средствами MS Excel.

Ключевые слова: прогнозирование, социальная сфера, культура, тренд, тенденция.
Эффективное функционирование образования, культуры, здравоохране- ния, туризма и отдыха, ЖКХ, экологии и спорта (социальной сферы в це- лом) всегда было целью стран с развитой экономикой. В последнее десяти- летие Россия уделяет большое внимание этим отраслям.

2014 год в России является годом культуры, поэтому прогнозирование показателей этой сферы особо актуально. Высокое качество прогнозов и планов оказывает весомый вклад в общественное развитие.

Культура оказывает большое влияние на духовную составляющую со- стояния общества. Показателями развития культуры являются число профес- сиональных театров, цирков, музеев, учреждений культуры клубного типа, число их посещений, а также количество массовых библиотек, тиражи книг, брошюр, газет и т.д. Не все из этих показателей рассчитываются на уровне Самарского региона (данные ежегодно предоставляются в самарском стати- стическом ежегоднике), но на уровне страны они ежегодно отслеживаются.

К учреждениям культуры принято относить клубы, библиотеки, дома культуры, театрально-зрелищные предприятия и объекты искусства: театры, цирки, кинотеатры, концертные залы.

Рассмотрим основные задачи прогнозирования сферы культуры. Во-пер- вых, это поддержание работы сетей всех учреждений культуры. Во-вторых, увеличение творческих возможностей профессиональных и самодеятельных коллективов. В-третьих, сохранение и развитие народного художественного творчества, народных промыслов и традиционной культуры (по моему мне-




^ Студент кафедры Математики и бизнес-информатики.