Экзамен Понятие информации и данных
 Скачать 421.5 Kb.
|
|
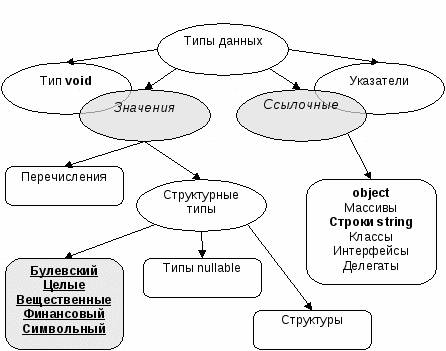
Экзамен 1. Понятие информации и данных. 1. Данные - это совокупность сведений, зафиксированных на определенном носителе в форме, пригодной для постоянного хранения, передачи и обработки. Преобразование и обработка данных позволяет получить информацию. И 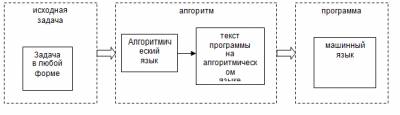 нформация - это результат преобразования и анализа данных. Отличие информации от данных состоит в том, что данные - это фиксированные сведения о событиях и явлениях, которые хранятся на определенных носителях, а информация появляется в результате обработки данных при решении конкретных задач. Например, в базах данных хранятся различные данные, а по определенному запросу система управления базой данных выдает требуемую информацию.2. Способы представления и обработки данных. Для того, чтобы использовать ЭВМ для обработки данных, необходимо располагать некоторым способом представления данных. Способ представления данных будет зависеть от того, для кого эти данные предназначены: для человека (внешнее представление) или для ЭВМ (внутреннее представление). Во внутреннем представлении данные могут быть описаны в аналоговой (непрерывной) или цифровой (дискретной) формах. В соответствии с этим различают аналоговые и цифровые ЭВМ. Практически все используемые ЭВМ в настоящее время являются цифровыми. Таким образом, любые данные в современных ЭВМ представляются в виде целых чисел. Любые виды данных, обрабатываемых на ЭВМ, могут быть сведены к совокупности простейших форм: набор символов (текст), звук (мелодия), изображение (фотографии, рисунки, схемы), вещественные и целые числа (числовая информация). Каждый такой вид данных должен быть некоторым универсальным образом представлен в виде набора целых чисел. Правила такого представления разрабатываются научными институтами и оформляются в виде стандартов. Во внешнем представлении все данные хранятся в виде файлов. Во многих случаях требуется ещё более высокий уровень организации данных на внешнем уровне, тогда данные группируются в базы данных (см. рис.). 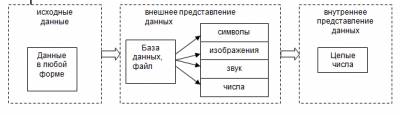 Рис. Уровень представления обработки данных Задачи по обработке данных предполагают также способы описания процесса самой обработки. Процедуры обработки данных также представляются на внешнем и внутреннем уровне. На внутреннем уровне каждая такая процедура представляет собой последовательность логических операций с целыми числами, и называется программой. Сами логические операции кодируются с помощью средств машинного языка. На внешнем уровне процедуры представляются в виде алгоритма. Конкретный вид алгоритма зависит от используемого алгоритмического языка.Таким образом, решение любых задач с помощью ЭВМ в конечном счёте сводится к двум взаимосвязанным проблемам: цифровому представлению данных и алгоритмическому представлению способов обработки данных. 3. Состав языка программирования. Состав языка: Символы:
Лексемы:
Выражения- правило вычисления значения Операторы:
4. Классификация языков программирования по Хомскому 5. Системы счисления. Особенности перевода из двоичной в шестнадцатеричную систему счисления и обратно. Систе́ма счисле́ния -символический метод записи чисел, представление чисел с помощью письменных знаков. Перевод чисел из двоичной системы счисления в шестнадцатеричную. Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи. Решаем показательное уравнение: 16 = 2i . Так как 16 = 24, то i = 4 бита. Каждый разряд шестнадцатеричного числа содержит 4 бита информации. Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями. Затем надо преобразовать каждую группу в шестнадцате-ричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр.
В результате имеем: А16 = 2916.
Получаем: А16 = 0,D416. Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей 6. Системы счисления. Особенности двоично-десятичной системы счисления. Систе́ма счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков. В компьютерной технике очень часто используется двоичная система счисления. Такую систему очень легко реализовать в электронике (полупроводниковые транзисторы и микросхемы), так как для неё требуется всего два устойчивых состояния (0 и 1) 7. Основные операции, выполняемые процессором. Процессор - это центральное устройство компьютера. Он выполняет находящиеся в оперативной памяти команды программы и "общается" с внешними устройствами благодаря шинам адреса, данных и управления, выведенными на специальные контакты корпуса микросхемы. Производительность (быстродействие) ПК– возможность компьютера обрабатывать большие объёмы информации. Определяется быстродействием процессора, объёмом ОП и скоростью доступа к ней Производительность (быстродействие) процессора – количество элементарных операций выполняемых за 1 секунду. Тактовая частота процессора (частота синхронизации)- число тактов процессора в секунду, а такт – промежуток времени (микросекунды) за который выполняется элементарная операция (например сложение). Таким образом Тактовая частота- это число вырабатываемых за секунду импульсов, синхронизирующих работу узлов компьютера. Именно ТЧ определяет быстродействие компьютера Разрядность процессора– max длина (кол-во разрядов) двоичного кода, который может обрабатываться и передаваться процессором целиком. Разрядность связана с размером специальных ячеек памяти – регистрами. Регистр в 1байт (8бит) называют восьмиразрядным, в 2байта – 16-разрядным и тд. Высокопроизводительные компьютеры имеют 8-байтовые регистры (64разряда) Время доступа - Быстродействие модулей ОП, это период времени, необходимый для считывание min порции информации из ячеек памяти или записи в память. Современные модули обладают скоростью доступа свыше 10нс Объем памяти (ёмкость)– max объем информации, который может храниться в ней. Плотность записи– объем информации, записанной на единице длины дорожки (бит/мм) Скорость обмена информации– скорость записи/считывания на носитель, которая определяется скоростью вращения и перемещения этого носителя в устройстве 8. Сложение двоичных чисел в прямом и обратном коде 9. Сложение двоичных чисел в прямом и дополнительном коде. Сложение и вычитание чисел в обратном и дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Общей для этих кодов особенностью (и очень удобной особенностью) является лишь то, что при поразрядном сложении чисел разряды, изображающие знаки чисел рассматриваются как равноправные разряды двоичного числа, которые складываются друг с другом и с единицей переноса из предыдущего разряда числа по обычным правилам арифметики. Различия же обратного и дополнительного кодов связаны с тем, что делается с единицей переноса из старшего разряда (изображающего, как неоднократно говорилось, знак числа). При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном коде эту единицу надо прибавить к младшему разряду результата.
а) В обратном коде
Умножение и деление двоичных чисел производится в ЭВМ в прямом коде, а знаки их используются лишь для определения знака результата. 10. Особенности обработки чисел с фиксированной запятой, имеющих знак.Число с фиксированной запятой — формат представления вещественного числа в памяти ЭВМ в виде целого числа. Если не требуется, чтобы какие-либо конкретные дробные числа входили в разрядную сетку, программисты обычно выбирают {\displaystyle z=2^{-f}} — это позволяет использовать в операциях умножения и деления битовые сдвиги. 11. Битовые операции. Логическое умножение. Битовая операция- некоторые операции над цепочками битов, в программировании, как правило, рассматриваются лишь некоторыми виды этих операций: логические побитые операции и битовые сдвиги. В системе команд микроконтроллеров AVR есть несколько битовых операций, которые трудно однозначно отнести к разделу только логических операций, они вполне могут найти себе место и в разделе арифметических операций (вернее, они там и находятся). Таких операций три: — логический сдвиг — арифметический сдвиг — циклический сдвиг через бит переноса Мы рассмотрим только операции, относящиеся к логическому сдвигу, а операции арифметического и циклического сдвига — в статьях по командам микроконтроллера. Битовые операции сдвига, относящиеся к логическому сдвигу: — логический сдвиг влево — логический сдвиг вправо Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания. Если перейти от записи высказываний на естественном языке к их записи на формальном языке алгебры высказований. В ней операцию логического умножения принято обозначать знаком «&» либо «^». Образуем составное высказывание F, которое получиться в результате конъюнкции двух простых высказываний: F = A&B С точки зрения алгебры высказываний мы записали формулу функции логического умножения, аргументами которого являются логические переменные А и В, которые могут принимать значения «истина» (1) и «ложь» (0). Сама функция логического умножения F также может принимать лишь два значения «истина» (1) и «ложь» (0). Значение логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов.
Логическое сложение
Исключающее« ИЛИ» (или сложение по модулю 2) — это бинарная операция, результат действия которой равен 1, если число складываемых единичных битов нечётно и равен 0, если чётно. Другими словами, если оба соответствующих бита операндов равны между собой, двоичный разряд результата равен 0; в противном случае, двоичный разряд результата равен 1. Логическое отрицание или инверсия: Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. 15. Константа в языке программирования. Назначение. Особенности применения Константа — это ограниченная последовательность символов алфавита языка, представляющая собой изображение фиксированного (неизменяемого) объекта. Константы бывают числовые, символьные и строковые. Числовые константы делятся на целочисленные и вещественные Литеральная константа - это константа (число, строковое выражение, дата), расположенная непосредственно в коде. Например: X = Y + 2 Здесь число 2 является литеральной константой. Именованная константа, как правило, объявляется в начале модуля или процедуры (аналогично переменной) и предназначена для удобства читания и понимания программного кода. |
