Экзамен. Анализ временных рядов. Билеты (гр. УЗКБ_18) (1). Экзаменационные билеты на экзамен по дисциплине Анализ и прогнозирование временных рядов Распределение вопросов по билетам

• Название: Экзаменационные билеты на экзамен по дисциплине Анализ и прогнозирование временных рядов Распределение вопросов по билетам
• Дата: 01.04.2022
• Размер: 31.49 Kb.
• Имя файла: Экзамен. Анализ временных рядов. Билеты (гр. УЗКБ_18) (1).docx
• Тип: Экзаменационные билеты; #434099

Экзаменационные билеты на экзамен по дисциплине

Анализ и прогнозирование временных рядов
Распределение вопросов по билетам

Номер билета совпадает с номером студента в электронном журнале группы

№ билета	№ вопроса 1	№ вопроса 2	№ задачи
1	2	24	1
2	3	23	2
3	4	22	3
4	5	21	4
5	6	20	5
6	7	19	6
7	8	18	7
8	9	17	8
9	10	16	9
10	11	15	1
11	12	14	2
12	13	13	3
13	14	12	4
14	15	11	5
15	16	10	6
16	17	9	7
17	18	8	8
18	19	7	9

Вопросы к экзамену

1. 
   Понятие и виды временных рядов. Примеры.
   
2. 
   Структура временных рядов.
   
3. 
   Виды моделей ВР. Как по графику временного ряда определить характер сезонности (аддитивный и мультипликативный)?
   
4. 
   Свойства случайной компоненты при верном выявлении других компонент.
   
5. 
   Этапы построения прогнозов по временным рядам.
   
6. 
   Процедуры предварительного анализа ВР.
   
7. 
   Выявления и устранение аномальных наблюдений во ВР. Метод Ирвина.
   
8. 
   Требования, предъявляемые к исходной информации и ее анализ.
   
9. 
   Методы обнаружения тренда. Метод сравнении средних уровней ряда.
   
10. 
    Сглаживание ВР. Метод простой скользящей средней.
    
11. 
    Сглаживание ВР. Метод взвешенной скользящей средней.
    
12. 
    Расчет динамических характеристик ВР.
    
13. 
    Автокорреляция ВР. Выявление автокорреляции. Анализ автокорреляционной функции.
    
14. 
    Закономерности, формирующие уровни ВР и соответствующие им модели ВР.
    
15. 
    Виды аппроксимирующих функций для построения моделей тренда. Интерпретация их параметров.
    
16. 
    Применение кривых роста.
    
17. 
    Расчет параметров модели методом наименьших квадратов.
    
18. 
    Критерии адекватности модели.
    
19. 
    Основные критерии точности модели.
    
20. 
    Проверка равенства математического ожидания остатков ВР нулю.
    
21. 
    Проверка условия случайности возникновения отдельных отклонений от тренда. Критерий поворотных точек.
    
22. 
    Проверка независимости остатков ряда (отсутствие автокорреляции).
    
23. 
    Проверка соответствие ряда остатков нормальному закону распределения.
    
24. 
    Получение точечного и интервального прогноза по линейному уравнению тренда.
    
25. 
    Выявление сезонной компоненты.
    
26. 
    Статистическое изучение сезонных колебаний с помощью индексов сезонности.
    

Задачи к экзамену по дисциплине

(соответствуют отдельным пунктам практического занятия и контрольной работы, но со своими исходными данными)

Задача 1.

Имеются следующие данные по уровням ряда:

t	Yt
1	38
2	44
3	43
4	50
5	42
6	47
7	57
8	55
9	54
10	58
11	64
12	63
13	68
14	72

Построить линейную модель тренды Y от t. Для оценки адекватности построенной модели проверить равенство математического ожидания остатков нулю.
Задача 2.

Имеются следующие данные по уровням ряда:

t	Yt
1	42
2	44
3	42
4	50
5	42
6	47
7	57
8	55
9	54
10	58
11	64
12	63
13	68
14	72

Построить линейную модель тренда Y от t. Для оценки адекватности построенной модели оценить случайность остаточной компоненты по критерию пиков.

Задача 3.

Имеются следующие данные по уровням ряда:

t	Yt
1	39
2	44
3	42
4	50
5	42
6	47
7	57
8	55
9	54
10	60
11	64
12	63
13	68
14	72

Построить линейную модель тренда Y от t. Для оценки адекватности построенной модели оценить независимость уровней ряда по коэффициенту автокорреляции остатков первого порядка.
Задача 4.

Имеются следующие данные по уровням ряда:

t	Yt
1	40
2	44
3	42
4	50
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	63
13	68
14	70

Построить линейную модель тренда Y от t. Для оценки адекватности построенной модели оценить соответствие ряда остатков нормальному закону распределения при помощи RS-критерия.

Задача 5.

Имеются следующие данные по уровням ряда:

t	Yt
1	40
2	44
3	42
4	50
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	63
13	68
14	70

Построить линейную модель тренда Y от t. Для оценки адекватности построенной модели оценить соответствие ряда остатков нормальному закону распределения при помощи RS-критерия.

Задача 6.

Имеются следующие данные по уровням ряда:

t	Yt
1	40
2	44
3	42
4	50
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	60
13	68
14	72

Построить линейную модель тренда Y от t. Оценить точности полученной модели на основе вычисления средней относительной ошибки аппроксимации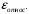

Задача 7.

Имеются следующие данные по уровням ряда:

t	Yt
1	38
2	44
3	42
4	50
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	63
13	68
14	70

Построить линейную модель тренда Y от t. С использованием полученной модели построить точечный прогноз на 3 шага вперед.

Задача 8.

Имеются следующие данные по уровням ряда:

t	Yt
1	41
2	44
3	42
4	50
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	63
13	68
14	70

Построить линейную модель регрессии Y от t. Для оценки адекватности построенной модели оценить соответствие ряда остатков нормальному закону распределения при помощи RS-критерия.
Задача 9.

Имеются следующие данные по уровням ряда:

t	Yt
1	43
2	44
3	42
4	48
5	42
6	47
7	57
8	52
9	54
10	60
11	64
12	62
13	68
14	72

Построить линейную модель тренда Y от t. Оценить точности полученной модели на основе вычисления средней относительной ошибки аппроксимации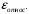