Электродинамика. Задача 45
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Электродинамика. Задача № 45 Перпендикулярно плоскости кольцевого тока (  ) радиусом ) радиусом 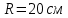 проходит изолированный длинный провод так, что он касается кольца. Ток в проводе равен проходит изолированный длинный провод так, что он касается кольца. Ток в проводе равен 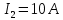 . Найдите суммарную напряженность магнитного поля в центре кольца. . Найдите суммарную напряженность магнитного поля в центре кольца.Дано:   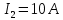 Найти: 𝐻−? Решение: Найдем отдельные вклады в индукцию магнитного поля в точке  (центр окружности), созданные каждым проводником с током на основании закона Био-Савара- Лапласа: (центр окружности), созданные каждым проводником с током на основании закона Био-Савара- Лапласа: (1) (1)где  – вектор, равный по модулю длине – вектор, равный по модулю длине 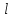 проводника и совпадающий по направлению с током, проводника и совпадающий по направлению с током,  – сила тока, – сила тока,  – радиус-вектор, проведенный от середины элемента проводника к точке, напряженность магнитного поля в которой определяется. – радиус-вектор, проведенный от середины элемента проводника к точке, напряженность магнитного поля в которой определяется.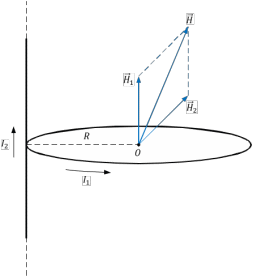 Рисунок 1 Для бесконечного проводника с током 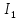 , текущим на расстоянии , текущим на расстоянии 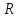 от точки от точки  , воспользуемся формулой: , воспользуемся формулой: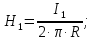 Для витка с током 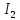 напряженность в центре напряженность в центре  : : На основании принципа суперпозиции магнитных полей: 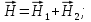 Модуль напряженности  по теореме Пифагора равен: по теореме Пифагора равен: (2) (2)Численно: 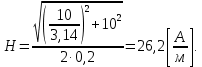 Ответ: 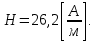 Задача № 55 Рамка гальванометра длиной  , шириной , шириной 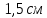 , содержащая , содержащая  витков тонкой проволоки, находится в магнитном поле с индукцией витков тонкой проволоки, находится в магнитном поле с индукцией 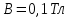 . Плоскость рамки параллельна линиям индукции. Найдите механический момент, действующий на рамку, когда по витку течет ток силой . Плоскость рамки параллельна линиям индукции. Найдите механический момент, действующий на рамку, когда по витку течет ток силой 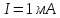 . .Дано: 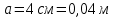 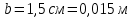 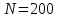 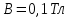 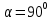  Найти:  Решение: На рамку с током в магнитном поле действует вращающий момент силы:  где 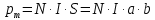 – магнитный момент прямоугольной рамки, – магнитный момент прямоугольной рамки,  - угол между векторами - угол между векторами  и и 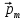 . .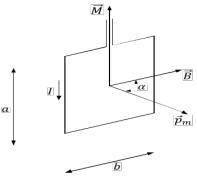 Рисунок 2 Численно: 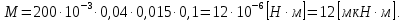 Ответ:  Задача № 65 Альфа-частица прошла ускоряющую разность потенциалов 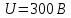 и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом 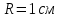 и шагом и шагом 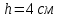 . Определить магнитную индукцию . Определить магнитную индукцию 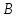 поля. поля.Дано:  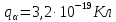 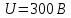   Найти: 𝐵−? Решение: Разложим скорость 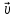 на две составляющие: на две составляющие: 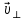 , перпендикулярно линиям индукции, и , перпендикулярно линиям индукции, и 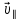 , параллельную им. Сила Лоренца будет непрерывно менять направление скорости частицы , параллельную им. Сила Лоренца будет непрерывно менять направление скорости частицы 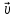 , сообщая ей в плоскости, перпендикулярной полю, нормальное (центростремительное) ускорение: , сообщая ей в плоскости, перпендикулярной полю, нормальное (центростремительное) ускорение: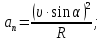  Рисунок 3 В результате частица будет описывать окружность радиуса 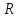 . Поскольку сила Лоренца играет роль центростремительной силы можно записать: . Поскольку сила Лоренца играет роль центростремительной силы можно записать: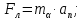 (4) (4)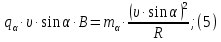 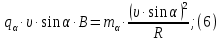 Откуда радиус орбиты частицы равен:  Синус угла  : :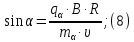 Вдоль поля частица будет двигаться с постоянной скоростью  . В результате наложения поступательного движения на круговое частица будет описывать в пространстве винтовую линию. . В результате наложения поступательного движения на круговое частица будет описывать в пространстве винтовую линию.Очевидно, что: 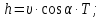 (9) (9)где 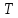 - период обращения частицы по окружности радиусом - период обращения частицы по окружности радиусом 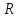 . Этот период равен: . Этот период равен: Тогда: 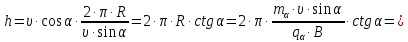 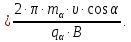 Отсюда косинус угла  : :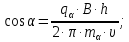 Воспользуемся основным тригонометрическим тождеством: 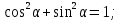 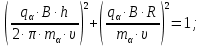 Отсюда квадрат скорости частицы: 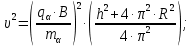 На основании закона сохранения энергии работа электростатических сил по перемещению альфа-частицы пошла на сообщение ей кинетической энергии: 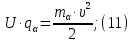 Ускоряющая разность потенциалов: 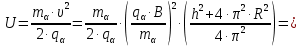  Откуда искомая индукция поля:  Численно: 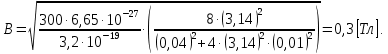 Ответ: 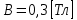 . .Оптика Задача № 5 Максимальная скорость точки, совершающей гармонические колебания, равна 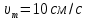 , максимальное ускорение , максимальное ускорение 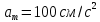 . Найти период и амплитуду колебаний. . Найти период и амплитуду колебаний.Дано: 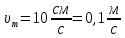  Найти: 𝑇−? 𝐴−? Решение: Уравнение гармонических колебаний имеет вид: 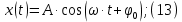 где  – амплитуда колебаний, – амплитуда колебаний,  - циклическая частота колебаний, - циклическая частота колебаний, 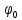 – начальная фаза колебаний. – начальная фаза колебаний.Скорость точки есть первая производная от уравнения движения по времени: 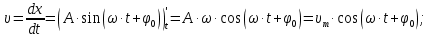 Откуда максимальная скорость материальной точки: 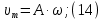 Ускорение есть вторая производная от уравнения движения по времени: 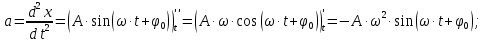 Максимальное ускорение: 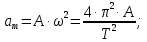 Угловая скорость:  Период колебаний:  Амплитуда колебаний: 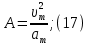 Численно: 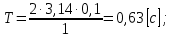 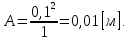 Ответ: 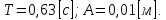 Задача № 25 На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом с длиной волны  . Диаметр пятого темного кольца Ньютона в отраженном свете равен . Диаметр пятого темного кольца Ньютона в отраженном свете равен 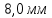 . Определить оптическую силу линзы и толщину слоя воздуха там, где видно пятое темное кольцо. . Определить оптическую силу линзы и толщину слоя воздуха там, где видно пятое темное кольцо.Дано:  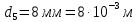  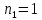  Найти: 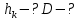 Решение: Между соприкасающимися поверхностями линзы и пластинки образуется клинообразный воздушный слой. Если на такую систему вертикально сверху падает пучок монохроматического света, то световые волны, отраженные от нижней поверхности линзы (луч  ) и верхней поверхности пластинки (луч ) и верхней поверхности пластинки (луч 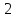 ), будут интерферировать между собой. ), будут интерферировать между собой.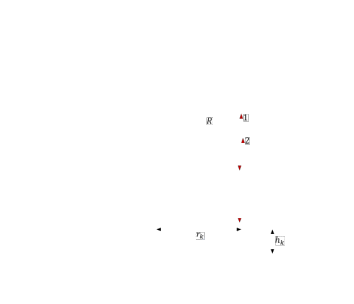 Рисунок 4 Оптическая разность хода между лучами  и и 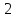 при интерференции в отраженном свете: при интерференции в отраженном свете: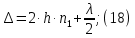 где 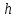 – толщина воздушного слоя, – толщина воздушного слоя,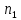 - показатель преломления воздуха. - показатель преломления воздуха.Темные полосы видны на тех участках пластины, для которых разность хода равна:  Приравнивая выражения для оптической разности хода лучей, получим: 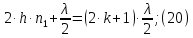 Отсюда ширина слоя, соответствующая  -ому радиусу темной зоны: -ому радиусу темной зоны: Определим радиус темной зоны из рисунка: 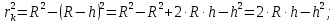 Так как слагаемое  , то его можно опустить: , то его можно опустить: Или: 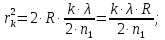 Так как диаметр темного кольца вдвое больше его радиуса, то можно записать:  Радиус кривизны линзы:  Воспользуемся формулой тонкой линзы:  где  - показатель преломления стекла, из которого изготовлена линза. - показатель преломления стекла, из которого изготовлена линза.Так как линза плосковыпуклая, то 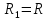 и и 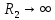 : :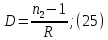 Окончательно:  Численно:  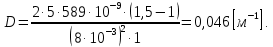 Ответ:  Задача № 35 На дифракционную решетку, содержащую  штрихов на штрихов на 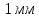 , падает нормально монохроматический свет , падает нормально монохроматический свет  . Найти общее число дифракционных максимумов, которое дает эта решетка. Определить угол отклонения последнего максимума. . Найти общее число дифракционных максимумов, которое дает эта решетка. Определить угол отклонения последнего максимума.Дано: 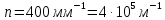  Найти:  Решение: Дифракционная картина на решетке (рис.5) определяется как результат взаимной интерференции волн, идущих от всех щелей, то есть в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.  Рисунок 5 Условие наблюдения дифракционных максимумов при дифракции на решетке: 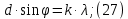 где  - постоянная дифракционной решетки, - постоянная дифракционной решетки,  – длина волны падающего света, – длина волны падающего света,  – угол дифракции, – угол дифракции,  – порядок спектра. – порядок спектра.При известном числе штрихов на 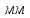 длины решетки постоянная дифракционной решетки равна: длины решетки постоянная дифракционной решетки равна: Выразим порядок спектра:  Наибольшему порядку соответствует  Тогда: 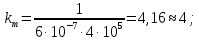 Общее число дифракционных максимумов с учетом центрального:  Угол дифракции, соответствующий последнему максимуму:  Ответ: 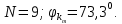 Задача № 45 На поверхность диэлектрика падает луч света. Угол преломления луча равен  , а отраженный луч при этом полностью поляризован. Определить скорость света в диэлектрике, его показатель преломления. Сделать чертеж. , а отраженный луч при этом полностью поляризован. Определить скорость света в диэлектрике, его показатель преломления. Сделать чертеж.Дано: 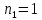 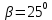 Найти:  Решение: Согласно закону Брюстера луч света, отраженный от диэлектрика, полностью поляризован в том случае, если тангенс угла падения равен относительному показателю преломления: 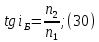  Рисунок 6 Отношение синуса угла падения к синусу преломления есть величина постоянная для двух данных сред: 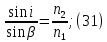 Тогда:  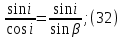 Угол падения:  Искомый показатель преломления:  Относительный показатель преломления среды показывает во сколько раз скорость распространения света в диэлектрике меньше скорости света в вакууме: 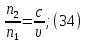 где 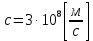 . .Искомая скорость света в диэлектрике равна: 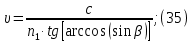 Численно: 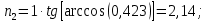  Ответ: 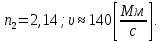 Задача № 55 Максимальная спектральная плотность излучательности абсолютно черного тела равна  . На какую длину волны она приходится? . На какую длину волны она приходится?Дано:  Найти: 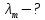 Решение: На основании первого закона Вина (закона смещения):  где 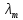 - длина волны, на которую приходится максимум спектральной плотности излучательности, - длина волны, на которую приходится максимум спектральной плотности излучательности,  - постоянная закона смещения Вина. - постоянная закона смещения Вина.Отсюда термодинамическая температура черного тела: 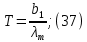 На основании второго закона Вина:  где  – значение спектральной плотности излучаемой при – значение спектральной плотности излучаемой при  , , 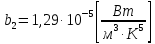 – постоянная. – постоянная.Тогда:  Искомая длина волны:  Численно:  Ответ: 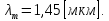 Задача № 65 На поверхность лития падает монохроматический свет (  ). Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов ). Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов  не менее не менее  . Определить работу выхода электрона. . Определить работу выхода электрона.Дано:   Найти:  Решение: Закон сохранения энергии, записанный Эйнштейном для фотоэффекта, состоит в утверждении, что энергия фотона, приобретенная электроном, позволяет ему покинуть поверхность проводника, совершив работу выхода. Остаток энергии реализуется в виде кинетической энергии теперь уже свободного электрона:  где  - постоянная Планка, - постоянная Планка,  - скорость света в вакууме, - скорость света в вакууме,  - масса электрона, - масса электрона,  - максимальная скорость электрона. - максимальная скорость электрона.Фотоэлектроны, покинувшие поверхность металла, обладают кинетической энергией. Этой энергии электронам достаточно, чтобы достичь анода и тем самым замкнуть цепь. Фототок исчезнет, когда:  где 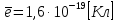 - заряд электрона. - заряд электрона.Перепишем уравнение Эйнштейна: 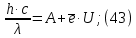 Отсюда искомая величина работы выхода электрона равна:  Численно: 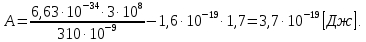 Ответ: 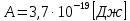 . .Атомная физика Задача № 55 Частица находится в возбужденном состоянии 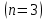 в одномерной потенциальной яме шириной в одномерной потенциальной яме шириной 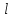 . В каких точках интервала . В каких точках интервала 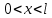 плотность вероятности нахождения частицы имеет экстремальные значения? плотность вероятности нахождения частицы имеет экстремальные значения?Дано:  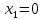 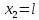 Найти:  Решение: Собственная волновая функция, описывающая возбужденное состояние частицы в потенциальном ящике, имеет вид: 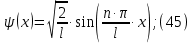 Плотность вероятности 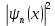 определяется выражением: определяется выражением: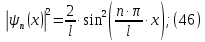 Для нахождения минимумов и максимумов вероятности найдем производную от выражения 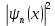 и приравняем ее к нулю: и приравняем ее к нулю: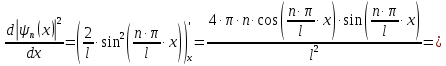  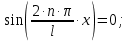 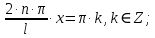 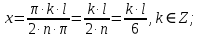 При 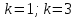 и и  в область в область 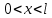 попадают попадают  – являющиеся точками максимума. – являющиеся точками максимума.При  и и 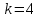 имеем точки минимума - имеем точки минимума - 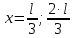 . .Ответ:  ; ; 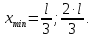 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Аникин А.И. Атомная физика: методические указания к выполнению контрольной работы №5 для студентов-заочников инженернотехнических специальностей / А.И. Аникин. – Архангельск: Изд-во АГТУ, 2007. – 38 с. 2. Филимоненкова Л.В. Оптика: методические указания к выполнению контрольного задания №4 для студентов заочного факультета / Л.В.Филимоненкова. – Архангельск: Изд-во АГТУ, 2005. – 43 с. 3. Филимоненкова Л.В. Электродинамика: методические указания к выполнению контрольного задания №3 для студентов-заочников инженерно-технических специальностей / Л.В.Филимоненкова, Н.С. Самылова, И.В. Шульгин. – Архангельск: Изд-во АГТУ, 2004. – 45 с. |
