ФИЗИКА. Электромагнетизм

• Название: Электромагнетизм
• Дата: 04.05.2023
• Размер: 2.73 Mb.
• Имя файла: ФИЗИКА.docx
• Тип: Закон; #1107384
• страница: 2 из 5

Пло́тность пото́ка эне́ргии — физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению потока. Часто вводят также вектор плотности потока энергии (так называемый вектор Умова), величина которого равна плотности потока энергии, а направление совпадает с направлением потока. В электродинамике вектор плотности потока электромагнитной энергии носит название вектора Пойнтинга.    (в системе СИ), где E и H — вектора напряжённости электрического и магнитного полей.

Любой источник света характеризуется своей интенсивностью — средним по времени значением величины вектора Пойнтинга:



Через значение напряжённости электрического поля её можно выразить следующим образом:

 ,где ε₀ — диэлектрическая постоянная,    — электродинамическая постоянная (скорость света в вакууме),    — показатель преломления среды, μ — магнитная проницаемость вещества. часто полагают --- 

10. Интерференция световых волн — это перераспределение светового потока в пространстве, которое происходит при наложение когерентных световых волн, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности.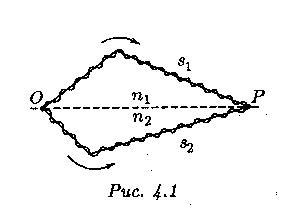

Когерентность и монохроматичность световых волн.

Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны - не ограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек.

Принцип суперпозиции (наложения) волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы каждой волны.

Интерференция волн – наложение двух (или нескольких) когерентных волн, в результате чего происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.

Когерентными называются волны одного направления одинаковой частоты и постоянной разности фаз.

Рассмотрим наложение двух когерентных волн, возбуждаемых точечными источниками (для простоты начальные фазы φ0=0):

ξ1(r,t)=A1·cos[ω(t-r1/υ)] ξ2(r,t)=A2·cos[ω(t-r2/υ)].

Разностьфаз этих колебаний равна: φ1-φ2=(ω/υ)·(r1-r2)=Δr·ω/υ=Δr·2π/υT=Δr·2π/λ, (115)

где Δr=r1-r2 - разность хода волн, λ=υT - длина волны.

1)если колебания происходят в одинаковой фазе, т.е. φ1-φ2=±2kπ (k=0,1,2...), (116) то наблюдается максимум интерференции. Приравниваем (115) и (116):

Δr·2π/λ=±2kπ.

Получаем условие максимума при интерференции: Δr=±kλ=±2k·λ/2 (k=0,1,2...) (117)

В этом случае A=A1+A2.

2)если колебания происходят в противофазе, т.е. φ1-φ2=±(2k+1)π (k=0,1,2...), (118) то наблюдается минимум интерференции. Приравниваем (115) и (117): Δr·2π/λ=±(2k+1)π

Получаем условие минимума при интерференции: Δr=±(2k+1)·λ/2 (k=0,1,2...) (118)

В этом случае A=| A1-A2 |



11. Способы наблюдения интерференции. Обычные источники света не являются когерентными, так как состоят из большого числа атомных излучателей. работающих независимо друг от друга. Для получения интерференционной картины прибегают к искусственным приемам. Сущность подобных методов заключается в том, что световой пучок, идущий от одного источника, делится на два пучка, которые друг другу когерентны и при наложении интерферируют. Например, в методе Юнга свет от точечного источника падает на непрозрачную преграду с двумя близкими узкими щелями, которые расщепляют исходный световой пучок на два когерентных пучка (см. рис. 2). Расчет интерференционной картины от 2 источн.

В области за преградой происходит наложение волн, идущих от щелей. Если в эту область поместить экран, то на его поверхности наблюдается интерференционная картина, представляющая собой чередование темных и светлых полос.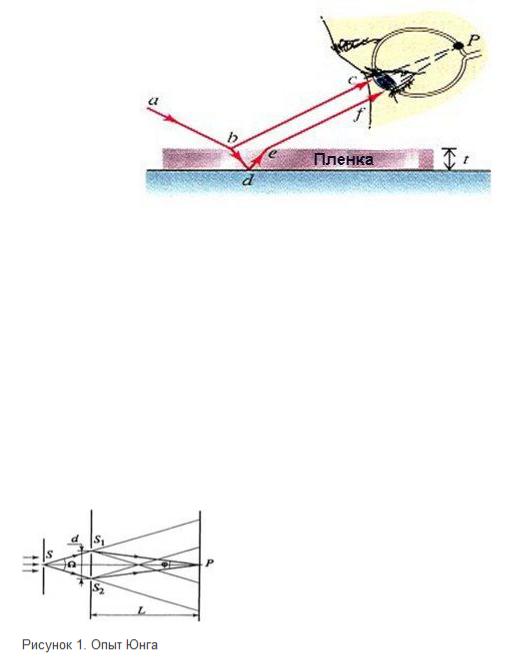

Интерференцию можно наблюдать и в естественных условиях. Например, окраска мыльных пузырей или тонких пленок бензина на поверхности воды объясняется интерференцией волн отраженных от наружной и внутренней поверхности пленки. Ход лучей в тонких пленках изображен на рис. 3.

12. Интерференция при отражении от тонких пластинок: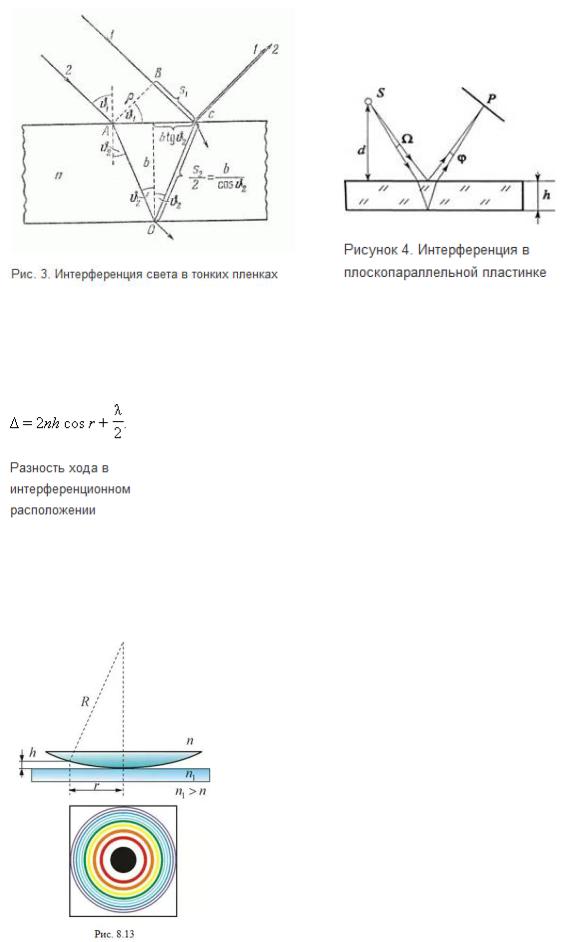



При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные световые волны, которые могут интерферировать.

Пусть на прозрачную плоскопараллельную пластинку падает параллельный пучок света, представленный на рис. 3 только одним лучом. Пластинка отбрасывает вверх два когерентных параллельных пучка света, из которых один образуется за счет отражения от верхней поверхности пластинки, второй — вследствие отражения от нижней поверхности. При входе в пластинку и при выходе из нее второй пучок претерпевает преломление. Кррме этих двух пучков пластинка отбросит вверх пучки, возникающие 'в результате трех-, пяти- и т. д. кратного отражения от поверхностей пластинки.



Кольца Ньютона

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла (рис. 8.13), называют кольцами Ньютона.

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны , разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания (рис. 8.13):

Здесь использовано условие. При наблюдении по нормали тёмные полосы, соответствуют толщине

, поэтому для радиуса m-го темного кольца

получаем 

(m = 0, 1, 2, …).

Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца

будут стягиваться к центру.

13. Дифракцией света принято называть отклонение от прямолинейного распространения света вблизи препятствий, например, при прохождении света через отверстие.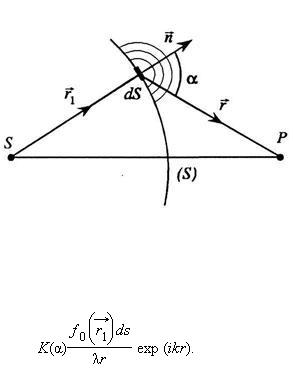



Принцип Гюйгенса-Френеля следует рассматривать как рецепт приближенного решения дифракционных задач. В основе его лежит допущение о том, что каждый элемент поверхности волнового фронта можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях (рис. 2.1.). Эти волны когерентны, так как они возбуждены одной и той же первичной волной. Результирующее поле в точке наблюдения P может быть найдено как результат интерференции вторичных волн. В качестве поверхности вторичных источников может быть выбрана не только поверхность волнового фронта, но и любая другая замкнутая поверхность. При этом фазы и амплитуды вторичных волн определяются значениями фазы и амплитуды первичной волны.

В соответствии с принципом Гюйгенса–Френеля комплексная амплитуда поля в точке наблюдения P, обусловленная действием вторичных источников, заселяющих малый элемент поверхности ds, может быть записана в виде:

Френель предложил ориги­нальный метод разбиения волновой поверхности. Она разбивается на кольцевые зоны ∆S (см. рис.2.1), построенные так, что рассто­яния от краев соседних зон до точки P отличаются на   (длина световой волны в той среде, в которой распространяется вол­на). Колебания, приходящие в точку Р от аналогичных точек двух соседних зон, противополож­ны по фазе, так как разность хода от этих зон до точки Р равна  . При наложении эти колебания взаимно ослабляют друг друга. Результирующая амплитуда в точкеР выразится суммой:

А = А₁ – А₂ + А₃ – А₄ + … (2.1)

Величина амплитуды А_kзависит от площади ∆S_k k-й зоны и угла α_k между внешней нормалью к поверхности зоны и прямой, направленной из этой точки в точку Р .

Можно показать, что площадь ∆S не зависит от номера зоны. Площади всех зон Френеля равновелики и мощности излучения вторичных источников одинаковы. Вместе с тем с увеличением k возрастает угол α_k между нормалью к поверхно­сти и направлением в точку Р, что приводит к уменьшению интен­сивности излучения kй зоны в данном направлении, т.е. к уменьше­нию амплитуды А_kпо сравнению с амплитудами предыдущих зон. Ам­плитуда А_kуменьшается также вследствие увеличения расстояния от зоны до точки Р с ростом α. В итоге



Вследствие большого числа зон убывание А_kносит монотонный характер и приближенно можно считать, что

. (2.2)

Переписав (2.I) в виде:

(2.3)

обнаруживаем, что согласно (2.2) выражения в скобках равны нулю и уравнение (2.1) приводится к виду  .

Полученный результат означает, что, колебания, вызываемые в точке Р полностью открытой сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только полови­на центральной зоны Френеля. Следовательно, свет от источника S₀в точку Р распространяется в пределах очень узкого прямого канала, т.е. прямолинейно. Расчеты показывают, что при радиусе сферической волновой поверхности S, равном r₀ = 0,1 м, и длине световой волны  м радиус центральной зоны Френеля порядка 1,610^-4 м, т.е. в результате интерференции уничтожается действие всех зон, кроме первой.

14. 1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в



точке В амплитуда А=А1, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки Вбудет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного

источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

или



так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

15. Дифракция на одной щели.

Рассмотрим дифракцию плоской монохроматической волны на щели, плоскость которой перпендикулярна направлению распространения волны.



Все вторичные источники в плоскости щели имеют одинаковую фазу. Поэтому при вычислении фазы излучения в точке наблюдения на экране за щелью остается учесть разность фаз, которая "набегает" от щели до экрана. Будем считать, что экран находится далеко от щели, что соответствует дифракции Фраунгофера. Подробнее дифракция Фраунгофера обсуждается ниже. Если экран далеко, то можно считать, что точки на пунктирной прямой   (рис. 31) одинаково удалены от точки наблюдения. Тогда для участка щели с координатой   расстояние до точки

наблюдения равно   плюс несущественная константа.

С изменением y-координаты линейно меняется расстояние до экрана, а значит - фаза поля, и угол поворота комплексной амплитуды на комплексной плоскости. Если мы мысленно разобьем

щель на тонкие полоски одинаковой ширины  , то одинаковые по модулю комплексные амплитуды от соседних полосок в точке наблюдения будут развернуты друг относительно друга на равные

углы  .

16. Дифракция Фраунгофера на дифракционной решетке.

Одномерная дифракционная решетка — система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Распределение интенсивности в дифракционном спектре каждой щели определяется направлением дифрагированных лучей и дифракционные картины, создаваемые каждой щелью будут одинаковыми.

Су 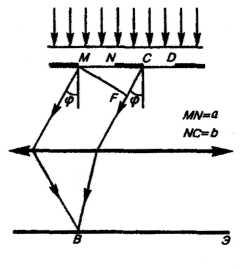ммарная дифракционная картина естьрезультат взаимной интерференции волн, идущих от всех щелей — в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света. идущих от всехшелей.

Еслиa— ширина каждой щели; b— ширина непрозрачных участков между щелями, то величина d = a + b называется постоянной (периодом) дифракционной решетки.

где No— число щелей, приходя­щееся на единицу длины.

Разности хода Δ лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки:

Δ = CF = (a + b)sinφ= dsinφ.

Очевидно, что в тех направлениях, в которых ни одно из щелей не распро­страняет свет, он не будет распространяться и при двух щелях, т.е. прежниiе (главные) минимумы интенсивности будут наблюдаться в направлениях asinφ=mλ (т =1,2,3,...). Кроме того, вследствие взаимной интерферен­ции, в направлениях, определяемых условием dsinφ = ±(2m + 1)λ/2 световые лучи, посылаемые двумя соседними щелями, будут гасить друг друга — воз­никнут дополнительные минимумы. Наоборот, действие одной щели будет усиливать действие другой, если dsinφ = ±2mλ/2 (m = 1,2,3,...) — условие главных максимумов.

В обшем случае, если дифракционная решетка состоит из N щелей, то:

• 
  условие главных максимумов: dsinφ = ±mλ/2 (m = 1,2,3,...)
  
• 
  условие главных минимумов: asinφ = ±mλ/2 (m = 1,2,3,...)
  

• 
  между двумя главными максимумами располагается N-1 дополнительных минимумов, разделенных вторичными максимумами, создающими слабый фон. Условие дополнительных минимумов: dsinφ = ± m'λ/N, (где m'может принимать все целочисленные значения, кроме О, N, 2N,... при которых данное условие переходит в условие главных максимумов).
  

Амплитуда главного максимума есть сумма амплитуд колебаний от каждой щели А_max = NA₁. Поэтому, интенсивность главного максимума в N²раз больше интенсивности I₁, создаваемой одной щелью в направлении главного максимума: I_max = N²I₁.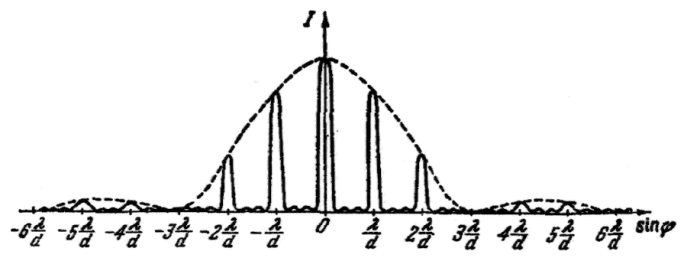



Например, на рисунке представлена ди­фракционная картина для N = 4. Пунктирная кривая изображает интенсивность от одной щели, умноженную на N².

П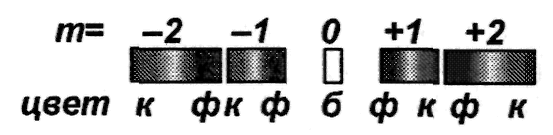



отложение главных максимумов зависит от длины волны λ, поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная — наружу. Поэтому дифракционная решетка может быть использована как спектральный прибор для разложения света в спектр и измерения длин волн.