Курсовая работа поперечное распространение эм волн в намагниченной плазме. ЭПиВкрсч. Электромагнитные поля и волны
 Скачать 126.95 Kb. Скачать 126.95 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕТРОНИКИ (ТУСУР) Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧиКР) ПОПЕРЕЧНОЕ РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В НАМАГНИЧЕННОЙ ПЛАЗМЕ Курсовая работа по дисциплине «Электромагнитные поля и волны» Выполнил студент гр. 150 ____________ Полянский К.А. (подпись) «____»____________2022г. (дата) Руководитель Профессор кафедры СВЧиКР: ________ ____________ А.Е. Мандель (оценка) (подпись) «____» ____________2022 г. (дата) Реферат Курсовая работа 18 с., 1 рис., 3 источника. ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ, ПЛАЗМА, ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ, ПОПЕРЕЧНОЕ РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В НАМАГНИЧЕННОЙ ПЛАЗМЕ. В данной работе в качестве объекта исследования выступает распространение электромагнитных волн в намагниченной плазме Целью работы является изучение поперечного распространения электромагнитных волн в намагниченной плазме, ее свойств и параметров. В процессе выполнения данной работы было изучено продольное распространение электромагнитных волн в анизотропной среде – намагниченной плазме. Также были решены уравнения Максвелла для намагниченной плазмы; рассчитаны тензор, фазовые скорости волн круговой поляризации правого и левого направлений вращения и угол поворота вектора при распространении 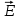 электромагнитной волны в продольно намагниченной плазме. электромагнитной волны в продольно намагниченной плазме.Пояснительная записка выполнена в текстовом редакторе Microsoft Word 2016. Министерство образования и науки РФ ТОМСКИЙ ИНСТИТУТ АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧиКР) УТВЕРЖДАЮ Зав.кафедрой СВЧ и КР _____________Шарангович С.Н. 2022г. ЗАДАНИЕ 13 на курсовую работу по дисциплине «Электромагнитные поля и волны» студенту группы 150 Полянскому К.А. 1. Тема работы: Продольное распространение электромагнитных волн в намагниченной плазме. 2. Срок сдачи законченной работы: 3. Исходные данные: 3.1. Концентрация электронов в плазме Ne= 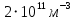 3.2. Величина постоянного магнитного поля приложенного к плазме 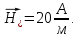 3.3. Частота электромагнитной волны 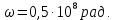 3.4. Длина пути электромагнитной волны в плазме 1000м. 3.5. Заряд электрона 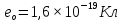 3.6.Масса электрона 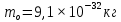 3.7.Магнитная постоянная 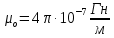 3.8.Диэлектрическая постоянная 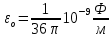 4. Перечень вопросов, подлежащих рассмотрению (содержание пояснительной записки) 4.1. Свойства плазмы в постоянном магнитном поле. 4.2. Электрические параметры намагниченной плазмы в постоянном магнитном поле. Уравнения Максвелла. 4.2.1. Расчет тензора диэлектрической проницаемости намагниченной плазмы 4.2.2. Решение системы уравнений Максвелла для намагниченной плазмы 4.3 Поперечное распространение электромагнитных волн в намагниченной плазме. Эффект Фарадея. 4.3.1. Расчет фазовых скоростей волн круговой поляризации правого и левого направлений вращения. 4.3.2.Расчет угла поворота вектора 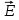 при распространении электромагнитной волны в продольно намагниченной плазме при распространении электромагнитной волны в продольно намагниченной плазме5. Перечень графического материала: 5.1. Представить график вращения вектора 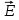 при распространении электромагнитной волны в продольно намагниченной плазме при распространении электромагнитной волны в продольно намагниченной плазме6. Список литературы 6.1. Гольдштейн Л.Д. Зернов Н.В. Электромагнитные поля и волны. М.: Сов. Радио, 1971,- 661c. 6.2. Баскаков С.И. Электродинамика и распространение радиоволн. М.: Высшая школа, 1992-416с. 6.3. Л.А.Боков, В.А. Замотринский, А.Е. Мандель Электродинамика и распространение радиоволн: Уч. пособие.. - Томск: ТУСУР, 2013. - 410. – Режим доступа: http://edu.tusur.ru/training/publications/3289. Дата выдачи задания Руководитель______________________ (подпись) Задание принял к выполнению_________________ (подпись студента) 1 Введение 6 2 Свойства плазмы в постоянном магнитном поле 7 3 Электрические параметры плазмы в постоянном магнитном поле. Уравнения Максвелла 8 3.1 Расчет тензора диэлектрической проницаемости намагниченной плазмы 9 3.2 Решение системы уравнений Максвелла для намагниченной плазмы 12 4 Поперечное распространение электромагнитных волн. Эффект Фарадея. 15 4.1 Расчет фазовых скоростей волг круговой поляризации правого и левого направлений вращения. 15 4.2 Расчет угла поворота вектора E при распространении электромагнитной волны в продольно намагниченной плазме. 15 5 График поляризационной структуры поля при поперечном распространении электромагнитной волны в намагниченной плазме. 17 Заключение 18 Список использованной литературы 19 Содержание1 Введение 6 2 Свойства плазмы в постоянном магнитном поле 7 3 Электрические параметры плазмы в постоянном магнитном поле. Уравнения Максвелла 8 3.1 Расчет тензора диэлектрической проницаемости намагниченной плазмы 9 3.2 Решение системы уравнений Максвелла для намагниченной плазмы 12 4 Поперечное распространение электромагнитных волн. Эффект Фарадея. 15 4.1 Расчет фазовых скоростей волг круговой поляризации правого и левого направлений вращения. 15 4.2 Расчет угла поворота вектора E при распространении электромагнитной волны в продольно намагниченной плазме. 15 5 График поляризационной структуры поля при поперечном распространении электромагнитной волны в намагниченной плазме. 17 Заключение 18 Список использованной литературы 19 1 ВведениеНаряду с изотропными средами существуют и такие, которые в разных направлениях обнаруживает различные свойства. Эти среды называются анизотропными. В анизотропных средах каждая проекция векторов 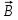 и и 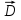 в общем случае может зависеть от трех проекций вектора в общем случае может зависеть от трех проекций вектора 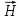 или или 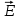 соответственно. Поэтому для них справедливы следующие равенства: соответственно. Поэтому для них справедливы следующие равенства: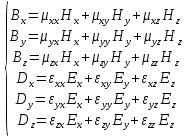 (1.1) (1.1)При введении тензоров магнитной и диэлектрической проницаемости уравнения (1.1) приобретают вид: 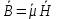 ; ; 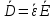 (1.2) (1.2)В общем случае для определения поля в анизотропной среде необходимо решать уравнения Максвелла в предположении, что магнитная и диэлектрические проницаемости являются тензорами вида: 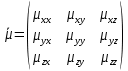 ; ; 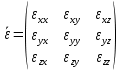 (1.3) (1.3)Энергия электромагнитного поля в анизотропной среде определяется выражением: 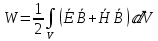 (1.4) (1.4)Типичным представителем анизотропной среды являются намагниченные постоянным полем феррит и ионизированный газ, т.е. плазма. Плазмой называется электрически нейтральный газ, в котором значительная часть атомов или молекул ионизирована. Плазма имеет ряд свойств, которые отличают его от обычных газов, содержащих одни нейтральные молекулы. Так, из-за наличия свободных зарядов плазма обладает большей, чем у обычных газов, электрической проводимостью. Свойства намагниченной плазмы различны для полей разного направления, т.е. под влиянием постоянного магнитного поля она может проявлять анизотропные свойства. Плазма содержит большое число заряженных частиц, которые в отсутствие постоянного магнитного поля (ненамагниченная плазма) движутся хаотически. Целью работы является изучение продольного распространения электромагнитных волн в намагниченной плазме, ее свойств и параметров. Область исследования: плазма. 2 Свойства плазмы в постоянном магнитном полеВ отличии от обычных газов, содержащих нейтральные частицы, плазма обладает большей электрической проводимостью за счет свободных частиц. Под воздействием постоянного магнитного поля, плазма может проявлять анизотропные свойства. Под влиянием электрического поля с напряженностью 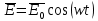 на каждый свободный электрон ненамагниченной плазмы действует сила на каждый свободный электрон ненамагниченной плазмы действует сила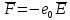 . (2.1) . (2.1)Пусть наряду с полем 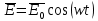 на плазму воздействует постоянное магнитное поле на плазму воздействует постоянное магнитное поле 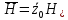 . Теперь, как только под влиянием электрического поля электрон приобретает скорость 𝑣̅, на него начинает действовать со стороны магнитного поля сила Лоренца . Теперь, как только под влиянием электрического поля электрон приобретает скорость 𝑣̅, на него начинает действовать со стороны магнитного поля сила Лоренца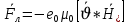 (2.2) (2.2)Из формулы (2.2) видно, что величина и направление силы Лоренца будут зависеть от взаимной ориентации векторов 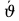 и и 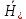 . . Предположим сначала, что после того, как электрону была сообщена начальная скорость векторов 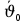 , вектор которой параллелен , вектор которой параллелен 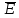 , электрическое поле исчезает. Тогда в зависимости от направления вектора , электрическое поле исчезает. Тогда в зависимости от направления вектора 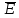 по отношению к по отношению к 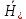 электроны будут перемещаться по различным траекториям. электроны будут перемещаться по различным траекториям. Если 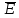 ∥ ∥ 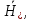 то согласно (2.2) сила Лоренца то согласно (2.2) сила Лоренца 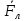 =0 и частицы двигаются прямолинейно вдоль силовых линий постоянного магнитного поля =0 и частицы двигаются прямолинейно вдоль силовых линий постоянного магнитного поля 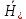 (как и при его отсутствии). При (как и при его отсутствии). При 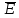 ⊥ ⊥ 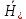 сила Лоренца имеет максимальное значение сила Лоренца имеет максимальное значение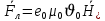 (2.3) (2.3)Таким образом, свойства намагниченной плазмы различны для полей разного направления. Иными словами, под воздействием постоянного магнитного поля плазма приобретает свойства анизотропной среды. 3 Электрические параметры плазмы в постоянном магнитном поле. Уравнения МаксвеллаПри движении плазмы относительно магнитного поля, или наоборот, в плазме должна возникнуть ЭДС индукции. Магнитное поле перемещается вместе с плазмой и может взаимодействовать с магнитными полями окружающего пространства, а также с потоками зарядов, движущихся от поверхности Земли в ионосферу, и наоборот. В объеме плазмы линии магнитного поля расположены на определенном расстоянии друг от друга. При этом если плазма расширяется, магнитное поле ослабляется, ибо расстояние между линиями индукции увеличивается. Если сжимается — линии индукции уплотняются и магнитное поле усиливается. Сжатие и расширение плазмы с «вмороженным» магнитным полем приводит к разным эффектам. Так, при сжимании плазмы магнитный поток хоть и остается постоянным, но индукция его возрастает пропорционально сжатию, что приводит к появлению очень сильного магнитного поля. При расширении плазмы магнитное поле также расширяется — уменьшается его индукция, что приводит к уменьшению энергии магнитного поля, «вмороженного» в плазму. Но поскольку полная энергия плазмы и магнитного поля в ней не изменяются, то увеличивается энергия плазмы — она нагревается. Плазма нагревается и при диффузии противоположных полей. Если направление магнитного поля вне плазмы противоположно направлению магнитного поля, «вмороженного» в плазму, взаимная диффузия приводит к тому, что поля гасят друг друга. Это приводит к уменьшению напряженности магнитного поля и к увеличению энергии плазмы. Уравнения Максвелла Система уравнений Максвелла для намагниченной плазмы свободной от источников поля имеет вид: 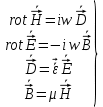 3.1 Расчет тензора диэлектрической проницаемости намагниченной плазмыДля вычисления тензора диэлектрической проницаемости намагниченной плазмы установим связь между вектором электрической индукции и напряженностью электрического поля. Пусть на плазму, находящуюся в постоянном магнитном поле, 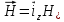 (3.1) (3.1)Действует несовпадающее с ним по направлению электрическое поле: 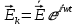 (3.2) (3.2)В этом случае движение каждого свободного электрона описывается уравнением 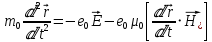 (3.3) (3.3)Так как радиус-вектор движущегося электрона будет изменяться в соответствии с законом изменения электрического поля, то решение уравнения (которое выше) следует искать в виде: 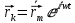 (3.4) (3.4)Подставим (3.2) и (3.3), в уравнение (3.4) и после сокращения на временной множитель получим 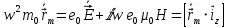 (3.5) (3.5)Умножая обе части (3.8) на число электронов N в единице объема и принимая во внимание 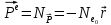 , имеем , имеем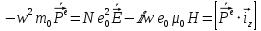 (3.6) (3.6)где 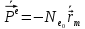 – это комплексная амплитуда вектора электрической поляризации. – это комплексная амплитуда вектора электрической поляризации.Для упрощения дальнейших рассуждений разделим обе части уравнения (3.6) на 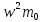 и перепишем его в виде и перепишем его в виде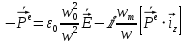 (3.7) (3.7)Здесь  и и  определяются соотношениями: определяются соотношениями: (3.8) (3.8)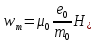 (3.9) (3.9)Уравнение (3.7) устанавливает связь между вектором электрической поляризации и вектором напряженности электрического поля на частоте 𝑤. Решая его, можно найти электрическую восприимчивость, а затем и диэлектрическую проницаемость намагниченной плазмы. Представим векторы 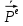 ̇ и ̇ и 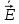 через их проекции на оси прямоугольной системы координат и вычислим векторное произведение: через их проекции на оси прямоугольной системы координат и вычислим векторное произведение: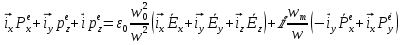 (3.10) (3.10)Приравнивая (3.10) одноименные проекции, получим 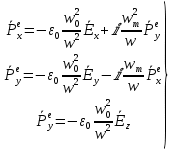 (3.11) (3.11)Система (3.11) позволяет определить проекции вектора электрической поляризации: 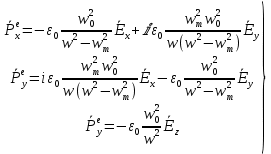 (3.12) (3.12)Амплитуда вектора электрической индукции согласно 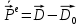 определяется равенством определяется равенством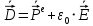 (3.13) (3.13)или в проекциях на оси прямоугольной системы координат: 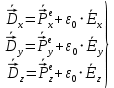 (3.14) (3.14)Подставляя значения 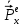 , , 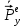 , ,  из (3.12) в (3.14) и группируя коэффициенты при одноименных проекциях вектора из (3.12) в (3.14) и группируя коэффициенты при одноименных проекциях вектора 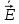 ̇, окончательно получаем: ̇, окончательно получаем: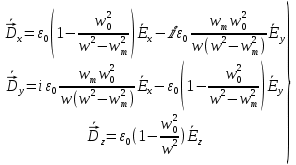 (3.15) (3.15)Отсюда видно, что каждая из проекций 𝐷𝑥̇ и 𝐷𝑦̇ определяется двумя проекциями вектора напряженности поля. Следовательно, диэлектрическая проницаемость является величиной тензорной. Сопоставляя (3.15) с общими выражениями, определим компоненты тензора диэлектрической проницаемости:  (3.16) (3.16)Введем обозначения: 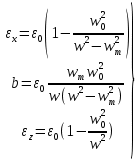 (3.17) (3.17)будем иметь: 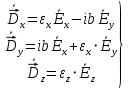 (3.18) (3.18)С учетом обозначений имеем тензор вида: 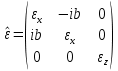 (3.19) (3.19)Подставив исходные данные в выражения (3.8), (3.9) и (3.17) получим: 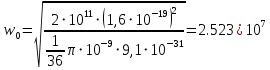 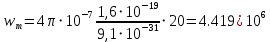 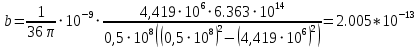 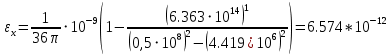 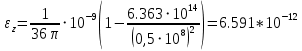 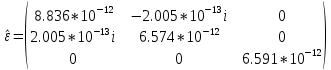 Компоненты тензора (3.18) зависят от величины постоянного магнитного поля. При изменении направления постоянного поля  на обратное изменяется знак у компоненты 𝑏. на обратное изменяется знак у компоненты 𝑏.3.2 Решение системы уравнений Максвелла для намагниченной плазмыМагнитная проницаемость намагниченной плазмы является скалярной величиной. Поэтому система уравнений Максвелла для намагниченной плазмы свободной от источников поля можем записать так: 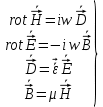 (3.20) (3.20)Принимая во внимание (3.18), выразим эти уравнения в декартовой системе координат: 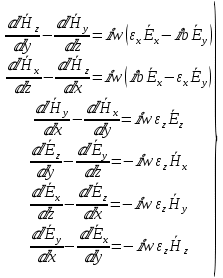 (3.21) (3.21)Пусть теперь плоская волна распространяется вдоль оси 𝑧 в плазме, намагниченной постоянным магнитным полем 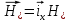 Полагая в (3.21)  ≡0, получаем: ≡0, получаем: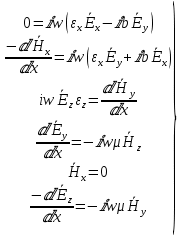 (3.22) (3.22)Решение системы (3.22) будем искать в виде: 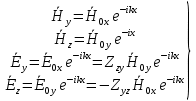 (3.23) (3.23)где 𝑘 – волновое число, а 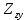 и и 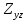 – волновые сопротивления. – волновые сопротивления. Подставляя (3.22) в (3.23) получим: 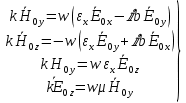 (3.24) (3.24)После исключения из первых двух уравнений 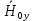 и и 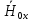 имеем: имеем: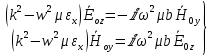 (3.25) (3.25)откуда волновое число: 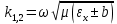 Подставляя 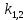 в одно из уравнений системы (2.24), находим: в одно из уравнений системы (2.24), находим: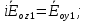 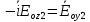 (3.26) (3.26)Выразим 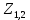 через систему уравнений (3.23): через систему уравнений (3.23):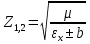 (3.27) (3.27)Вводя 𝑘1 и 𝑘2 в (3.23) и принимая во внимание (3.26) и (3.27) определяем компоненты векторов поля: 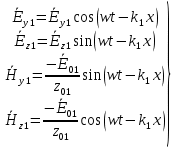 (3.28) (3.28)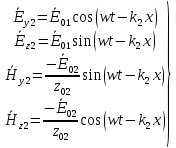 (3.29) (3.29)Видно, что плоская линейно поляризованная электромагнитная волна, попадая в намагниченную плазму, может быть разложена на две волны с круговой поляризацией с противоположным направлением вращения векторов. Одну из них описывает система уравнений (3.28), другую — (3.29). 4 Поперечное распространение электромагнитных волн. Эффект Фарадея.4.1 Расчет фазовых скоростей волг круговой поляризации правого и левого направлений вращения.Фазовые скорости волн правого и левого вращения равны: 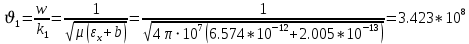 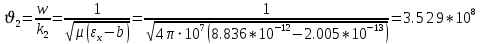 4.2 Расчет угла поворота вектора E при распространении электромагнитной волны в продольно намагниченной плазме.Полное поле имеет вид: 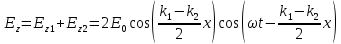 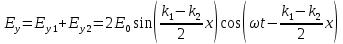 в каждый момент времени 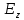 и и 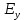 синфазны, угол наклона вектора E относительно оси z: синфазны, угол наклона вектора E относительно оси z: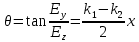 т.е. поле имеет линейную поляризацию, но плоскость поляризации медленно вращается при распространении волны. Это явление называется эффект Фарадея. Угол, на который поворачивается плоскость поляризации при прохождении волной единицы длины 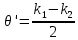 называется постоянная Фарадея. Среды, в которых наблюдается эффект Фарадея, называются гиротропными (вращающими). Этот эффект невзаимный, т.к. при изменении направления 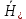 меняет знак 𝑏. Поскольку меняет знак 𝑏. Поскольку 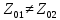 , поле 𝐻 имеет эллиптическую поляризацию. , поле 𝐻 имеет эллиптическую поляризацию.Подставим в формулу (4.3) числовые значения и найдем угол наклона 𝐸 относительно оси x: 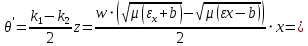 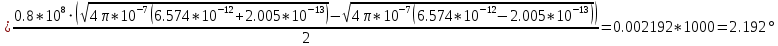 5 График поляризационной структуры поля при поперечном распространении электромагнитной волны в намагниченной плазме.Продольное распространение электромагнитной волны в намагниченной плазме сопровождается поворотом вектора напряженности электрического поля (рисунок 5.1) 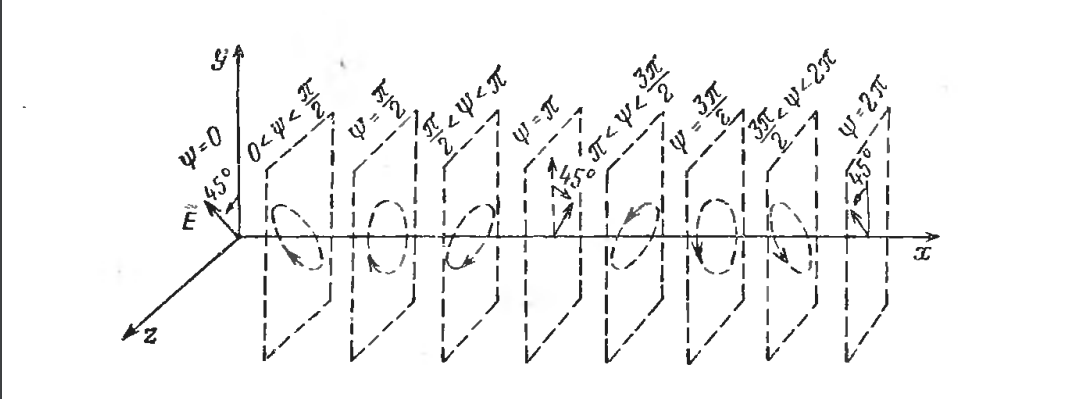 Рисунок 5.1 - График вращения вектора 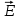 при распространении электромагнитной волны в продольно намагниченной плазме. при распространении электромагнитной волны в продольно намагниченной плазме.ЗаключениеВ результате выполнения курсовой работы было изучено поперечное распространение электромагнитных волн в намагниченной плазме, выступающей в качестве анизотропной среды. Анизотропия среды достигалась приложением электромагнитного поля к намагниченной плазме. В результате проделанной работы были рассчитаны: Тензор диэлектрической проницаемости намагниченной плазмы согласно пункту 4.2.1 технического задания (ТЗ); Фазовые скорости волн круговой поляризации правого и левого направлений вращения согласно пункту 4.3.1 ТЗ; Угол поворота вектора 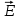 при распространении электромагнитной волны в продольно намагниченной плазме согласно пункту 4.3.2 ТЗ. при распространении электромагнитной волны в продольно намагниченной плазме согласно пункту 4.3.2 ТЗ.Построен график вращения вектора 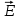 (рис.5.1) при распространении электромагнитной волны в продольно намагниченной плазме в соответствии с пунктом 5 ТЗ. (рис.5.1) при распространении электромагнитной волны в продольно намагниченной плазме в соответствии с пунктом 5 ТЗ.Список использованной литературыГольдштейн Л.Д. Зернов Н.В. Электромагнитные поля и волны. М.: Сов. Радио, 1971,- 661c. Баскаков С.И. Электродинамика и распространение радиоволн. М.: Высшая школа, 1992-416с. Л.А.Боков, В.А. Замотринский, А.Е. Мандель Электродинамика и распространение радиоволн: Уч. пособие.. - Томск: ТУСУР, 2013. - 410. – Режим доступа: http://edu.tusur.ru/training/publications/3289. Томск 2022 |
