|
|
Электронная цифровая подпись
Государственный университет телекоммуникаций
Учебно-научный институт защиты информации
Кафедра информационной и кибернетической безопасности
Прикладная криптология
О Т Ч Ё Т
по лабораторной работе № 16
ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ
Вариант № 6
Выполнил(ла): студент(ка) группы БСД-32
Фамилия И.О Голух Д.Р
Дата сдачи/защиты____________________
Провирила____________________________
Оценка______________________________
2018Выполнение работы
Задание 1. Для произвольного сообщения 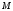 (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП Эль-Гамаля. Используйте хэш-функцию (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП Эль-Гамаля. Используйте хэш-функцию 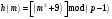 и параметры: простое число и параметры: простое число 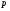 и первообразный элемент и первообразный элемент 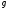 поля Галуа поля Галуа 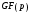 . .
Решение. Построим ЭЦП Эль-Гамаля для сообщения 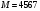 . .
Создание открытого и закрытого ключей. Сгенерируем открытый ключ 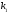 и закрытый ключ и закрытый ключ 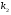 . Для этого: . Для этого:
выберем простое число 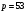 и первообразный корень и первообразный корень 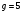 по модулю по модулю 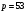 ; ;
выберем целое число  из интервала из интервала 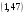 , например, , например, 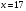 . .
вычислим значение 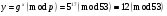 . .
открытый ключ 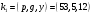 и закрытый ключ и закрытый ключ 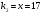 сформированы. сформированы.
Формирование ЭЦП с помощью закрытого ключа. Сформируем ЭЦП с помощью закрытого ключа. Для того чтобы подписать сообщение 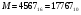
с помощью криптографической хэш-функции 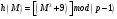 вычислим его хэш-код: вычислим его хэш-код:
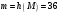 ; ;
выберем произвольное число 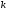 из отрезка из отрезка 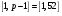 (рандомизатор) с условием НОД (рандомизатор) с условием НОД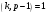 , например, , например, 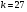 . .
вычислим 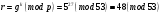 ; ;
вычислим 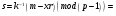
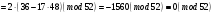 ; ;
подписью для сообщения 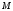 является пара является пара 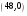 ; ;
пересылаем абоненту 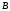 пару пару 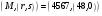 . .
Проверка подписи с помощью открытого ключа (верификация). Для проверки подписи сообщения 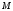
с помощью криптографической хэш-функции 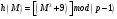 вычисляем хэш-код полученного документа: вычисляем хэш-код полученного документа: 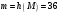 . .
проверяем равенство 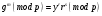 : :
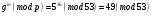 ; ;
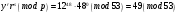 . .
Равенство выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.
Задание 2. Для произвольного сообщения 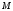 (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП DSA. Используйте хэш-функцию (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП DSA. Используйте хэш-функцию 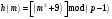 и простые числа и простые числа 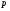 и и 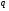 такие, чтобы такие, чтобы 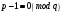 . .
Решение. Построим ЭЦП DSA для сообщения 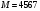 . .
Создание открытого и закрытого ключей. Сгенерируем ключевую пару: открытый ключ 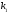 и закрытый ключ и закрытый ключ 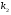 . Для этого: . Для этого:
выберем два простых числа 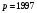 и и 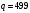 так, что так, что 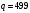 является делителем является делителем 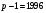 ( (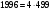 ); );
выберем целое число 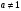 так, что так, что 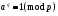 . Для этого выберем первообразный корень . Для этого выберем первообразный корень 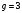 по модулю по модулю 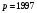 и вычислим и вычислим 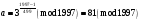 ; ;
выберем случайное целое число 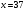 , , 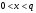 . .
вычислим значение 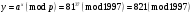 ; ;
Открытый ключ 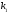 – четвёрка чисел – четвёрка чисел 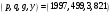 , закрытый ключ , закрытый ключ 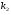 – число – число 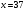 . .
Формирование ЭЦП с помощью закрытого ключа. Для того чтобы подписать сообщение 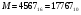
с помощью криптографической хэш-функции 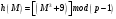 вычислим хэш-код вычислим хэш-код 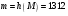 ; ;
выберем случайное число 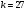 , , 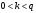 , , , , 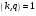 ; ;
вычислим 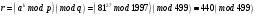 , ,
вычислим 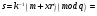
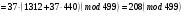 ; ;
подписью для сообщения 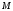 является пара является пара 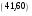 ; ;
пересылаем абоненту 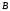 пару пару 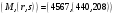 . .
Проверка подписи с помощью открытого ключа (верификация). Для проверки подписи сообщения 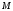
Проверим условия 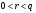 , , 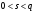 : : 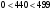 , , 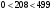 . .
с помощью криптографической хэш-функции 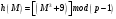 вычислим хэш-код полученного сообщения вычислим хэш-код полученного сообщения 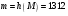 ; ;
вычислим
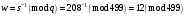 , ,
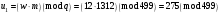 , ,
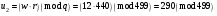 , ,
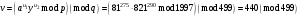
проверяем равенство 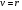 . .
Равенство 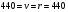 выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной. выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.
Задание 3. Для произвольного сообщения 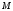 (длиной 16 бит), заданного в шестнадцатеричной системе счисления, построить ЭЦП RSA. Используйте хэш-функцию (длиной 16 бит), заданного в шестнадцатеричной системе счисления, построить ЭЦП RSA. Используйте хэш-функцию 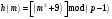 и (двузначные) простые числа и (двузначные) простые числа 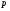 и и 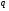 из первой сотни. из первой сотни.
Решение. Построим ЭЦП RSA для сообщения 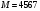 . .
Создание открытого и закрытого ключей. Сгенерируем открытый ключ 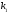 и закрытый ключ и закрытый ключ 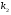 . Для этого: . Для этого:
Выберем два простых числа из первой сотни: 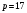 и и 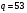 . .
Вычислим их произведение – число 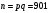 . .
Вычислим значение функции Эйлера 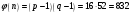 . .
Выберем число, взаимно простое с 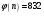 и такое, что и такое, что 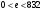 , например, число , например, число 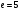 . .
Вычислим число 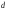 , обратное числу , обратное числу 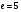 по модулю по модулю 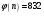 : :
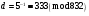
Открытый ключ 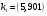 публикуется, а закрытый ключ публикуется, а закрытый ключ 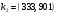 сохраняется в секрете. сохраняется в секрете.
Формирование ЭЦП с помощью закрытого ключа. Сформируем ЭЦП с помощью закрытого ключа. Для того чтобы подписать сообщение 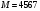
с помощью криптографической хэш-функции 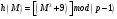 вычислим его хэш-код вычислим его хэш-код 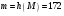 ; ;
зашифруем хэш на секретном ключе 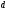 : : 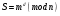 : :
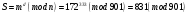 . .
пересылаем абоненту 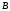 пару пару 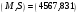 . .
Проверка подписи с помощью открытого ключа (верификация). Для проверки подписи сообщения 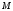
с помощью криптографической хэш-функции 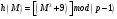 вычисляем хэш-код полученного документа: вычисляем хэш-код полученного документа: 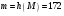 . .
расшифруем 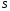 с помощью открытого ключа с помощью открытого ключа 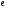 : : 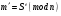 : :
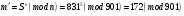 . .
Равенство 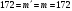 выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной. выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной. |
|
|
 Скачать 221.66 Kb.
Скачать 221.66 Kb.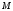 (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП Эль-Гамаля. Используйте хэш-функцию
(длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП Эль-Гамаля. Используйте хэш-функцию 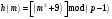 и параметры: простое число
и параметры: простое число 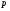 и первообразный элемент
и первообразный элемент 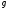 поля Галуа
поля Галуа 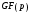 .
.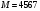 .
.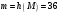 ;
;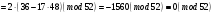 ;
;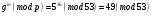 ;
;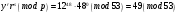 .
.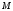 (длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП DSA. Используйте хэш-функцию
(длиной 16 битов), заданного в шестнадцатеричной системе счисления, построить ЭЦП DSA. Используйте хэш-функцию 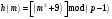 и простые числа
и простые числа 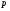 и
и 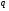 такие, чтобы
такие, чтобы 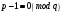 .
.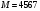 .
.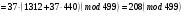 ;
;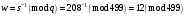 ,
,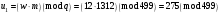 ,
,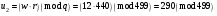 ,
,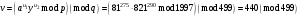
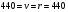 выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.
выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.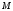 (длиной 16 бит), заданного в шестнадцатеричной системе счисления, построить ЭЦП RSA. Используйте хэш-функцию
(длиной 16 бит), заданного в шестнадцатеричной системе счисления, построить ЭЦП RSA. Используйте хэш-функцию 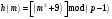 и (двузначные) простые числа
и (двузначные) простые числа 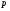 и
и 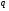 из первой сотни.
из первой сотни.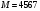 .
.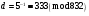
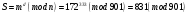 .
.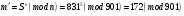 .
.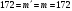 выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.
выполнено, т.е. в данном случае ЭЦП сообщения признаётся верной.
 и закрытый ключ
и закрытый ключ  . Для этого:
. Для этого: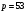 и первообразный корень
и первообразный корень 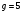 по модулю
по модулю  из интервала
из интервала 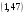 , например,
, например, 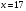 .
.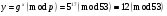 .
.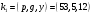 и закрытый ключ
и закрытый ключ 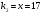 сформированы.
сформированы.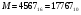
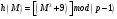 вычислим его хэш-код:
вычислим его хэш-код: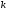 из отрезка
из отрезка 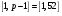 (рандомизатор) с условием НОД
(рандомизатор) с условием НОД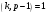 , например,
, например, 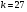 .
.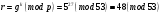 ;
;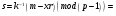
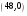 ;
;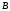 пару
пару 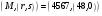 .
.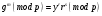 :
: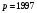 и
и 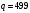 так, что
так, что 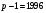 (
(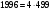 );
);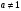 так, что
так, что 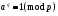 . Для этого выберем первообразный корень
. Для этого выберем первообразный корень 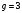 по модулю
по модулю 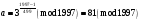 ;
;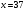 ,
, 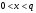 .
.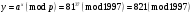 ;
;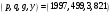 , закрытый ключ
, закрытый ключ 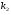 – число
– число 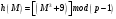 вычислим хэш-код
вычислим хэш-код 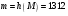 ;
;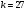 ,
, 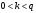 , ,
, , 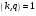 ;
;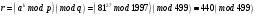 ,
,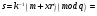
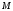 является пара
является пара 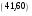 ;
; пару
пару 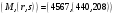 .
.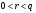 ,
, 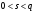 :
: 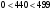 ,
, 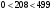 .
.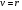 .
. 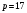 и
и 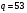 .
.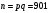 .
.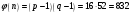 .
.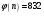 и такое, что
и такое, что 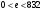 , например, число
, например, число 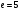 .
.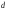 , обратное числу
, обратное числу 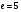 по модулю
по модулю 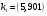 публикуется, а закрытый ключ
публикуется, а закрытый ключ 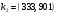 сохраняется в секрете.
сохраняется в секрете.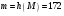 ;
;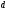 :
: 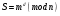 :
: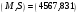 .
.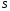 с помощью открытого ключа
с помощью открытого ключа 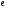 :
: 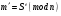 :
: