2.Примесные полупроводники
Полупроводники, в кристаллическую решетку которых введены атомы примесей с валентностью, отличающейся от валентности основных атомов, называются примесными. Электрическая проводимость, создаваемая введенной примесью, называется примесной проводимостью. Именно примесные полупроводники используются для изготовления всех элементов электроники. У них концентрация носителей заряда, вызванных наличием примеси, значительно превышает концентрацию собственных носителей заряда, поэтому электропроводимость проявляется при более низких температурах. Дело в том, что в рабочем интервале температур поставщиками свободных носителей заряда являются примеси. При их малой концентрации вероятность непосредственного перехода электронов от одного примесного атома к другому ничтожно мала. Но, однако, примеси могут либо поставлять электроны в зону проводимости полупроводника, либо принимать их с уровней его валентной зоны.
Под примесями в полупроводниковых химических соединениях понимаются не только включения атомов посторонних элементов, но и избыточные собственные атомы. Кроме того, роль примесей играют всевозможные дефекты кристаллической решетки: пустые узлы, атомы или ионы, оказавшиеся в междоузлиях решетки, дислокации или сдвиги, возникающие при пластической деформации кристалла, микротрещины и т.д.
В зависимости от валентности примеси делятся на донорные и акцепторные. Если валентность примесных атомов больше, чем основных, примесь является донорной, т.к. в этом случае у примесного атома образуется лишний электрон, не участвующий в ковалентной связи с основными атомами. Этот электрон связан со своим атомом только силой кулоновского взаимодействия. Энергия этой связи невелика (сотые доли электрон-вольта). Поскольку при комнатной температуре тепловая энергия электрона kT=0,026эВ, ионизация примесных атомов происходит уже при этой температуре. Лишний электрон отрывается от атома и становится свободным, т.е. примесные атомы выполняют роль доноров электронов.
С точки зрения зонной теории, донор – это примесный атом или дефект кристаллической решетки, создающий в запрещенной зоне энергетический уровень, занятый в невозбужденном состоянии электроном и способный в возбужденном состоянии отдать электрон в зону проводимости.
На рисунке 3.5 показан монокристалл четырехвалентного кремния, в кристаллическую решетку которого введено некоторое количество атомов примеси, например, пятивалентной сурьмы Sb. Атом примеси располагается в узле кристаллической решетки, четыре его валентных электрона участвуют в ковалентной связи с соседними атомами кремния аналогично существующим связям в основных атомах кристаллической решетки. Пятый же валентный электрон Sb такой связи установить не может, т.к. в атомах кремния все свободные связи (уровни) уже заполнены, и отправляется в «свободное плавание».
Атом примеси, потеряв один электрон, становится положительно заряженным ионом с единичным положительным зарядом. Он остается в узле кристаллической решетки и, в отличие от дырки, тоже имеющей единичный положительный заряд, не может перемещаться внутри кристалла, т.к. связан с соседними атомами полупроводника межатомными связями. Этот ион может только совершать колебательные явления около положения равновесия в узле кристаллической ячейки. При этом электрическая нейтральность кристалла не нарушается, т.к. заряд каждого электрона, перешедшего в зону проводимости, компенсируется положительно заряженным ионом примеси.
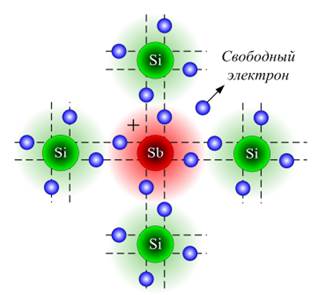
Рисунок 3.5 – Механизм действия донорной примеси
Такой вид примесной электропроводности, обусловленной наличием свободных электронов в зоне проводимости, называется электронной, или n-проводимостью, а сам полупроводник – электронным, или полупроводником n-типа. Энергетическая диаграмма такого полупроводника показана на рисунке 3.6. Как видно, наличие примеси в кристаллической решетке полупроводника характеризуется появлением локального энергетического уровня, лежащего в запрещенной зоне, – уровня донорной примеси. Он располагается на небольшом расстоянии от нижнего края («дна») зоны проводимости. Поскольку на один примесный атом в n-полупроводнике приходится 106 – 107 атомов основного вещества и расстояние между ними большое, то они практически не оказывают влияния друг на друга. Поэтому примесные донорные уровни не расщепляются, и на энергетической диаграмме присутствуют в виде одного уровня, на котором находятся все лишние валентные электроны, не участвующие в ковалентных связях. Энергетический интервал ΔWn называется энергией ионизации доноров. Для кремния, например, он составляет 0,05 эВ, а для германия – 0,01 эВ, поэтому у этих полупроводников при комнатной температуре практически все доноры ионизированы.
Наряду с ионизацией примеси в электронном полупроводнике происходит и тепловая генерация, в результате которой образуется пара носителей – электрон и дырка. Однако их количество при рабочей температуре гораздо меньше, чем количество электронов, образовавшихся за счет донорной примеси. Объясняется это двумя факторами. Во-первых, энергия, равная ширине запрещенной зоны ΔW, гораздо больше энергии ионизации донора ΔWn. Во-вторых, электроны донорных атомов занимают в зоне проводимости нижние энергетические уровни, и электроны, находящиеся в валентной зоне, в результате разрыва ковалентных связей могут перейти только на более высокие уровни зоны проводимости. Для такого перехода электрон должен обладать даже более высокой энергией, нежели в собственном полупроводнике. Поэтому в полупроводнике n-типа концентрация дырок на несколько порядков меньше концентрации электронов; соответственно в этом случае электроны называются основными носителями заряда, а дырки – неосновными.
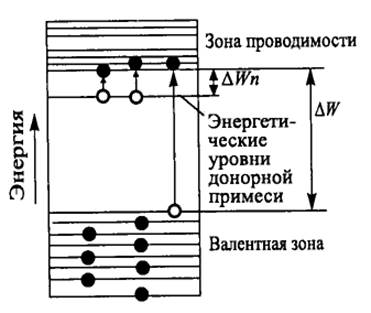
Рисунок 3.6 – Энергетическая диаграмма полупроводника n – типа
Кроме сурьмы, типичными донорами для кремния и германия являются мышьяк (As) и фосфор (P).
Если в кристаллическую решетку кремния ввести атомы трехвалентной примеси, например, индия, имеющего на наружной электронной оболочке три валентных электрона, то эти электроны образуют ковалентные связи только с тремя соседними атомами кремния из четырех (рисунок 3.7).
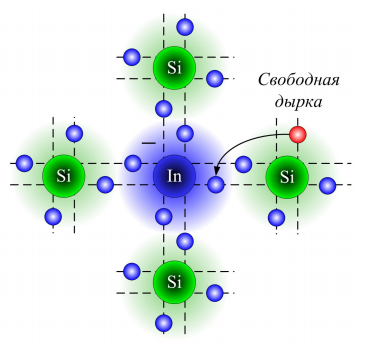
Рисунок 3.7 – Механизм действия акцепторной примеси
Одна из связей останется незаполненной из-за отсутствия у атома примеси необходимого электрона. При незначительном тепловом воздействии может произойти ее заполнение за счет электрона, перешедшего к атому примеси от соседнего основного атома. При этом атом примеси, приобретая лишний электрон, становится отрицательно заряженным ионом, а в основном атоме на том месте, откуда пришел электрон, возникает дырка. Она перемещается по связям основного вещества и, следовательно, принимает участие в проводимости полупроводника. Такая примесь, захватывающая электроны, называется акцепторной, проводимость – дырочной, или проводимостью р-типа, а сам полупроводник – дырочным, или полупроводником р-типа.
Для образования свободной дырки за счет перехода электрона от основного атома к атому примеси требуется значительно меньше энергии, чем для разрыва ковалентных связей кремния, поэтому основными носителями заряда в этом случае будут дырки, а неосновными – электроны.
С точки зрения зонной теории, акцептор – это примесный атом или дефект кристаллической решетки, создающий в запрещенной зоне энергетический уровень, свободный от электрона в невозбужденном состоянии и способный захватить электрон из валентной зоны в возбужденном состоянии.
На энергетической диаграмме полупроводника р-типа в запрещенной зоне появляется примесный уровень, расположенный на небольшом расстоянии от верхнего края («потолка») валентной зоны (рисунок 3.8). Этот уровень заполняется электронами, переходящими на него из валентной зоны, т.к. для такого перехода требуется незначительная энергия (ΔWp = 0,01 – 0,1 эВ). При комнатной температуре практически все акцепторы ионизированы, поэтому концентрация дырок примерно равна концентрации акцепторов.
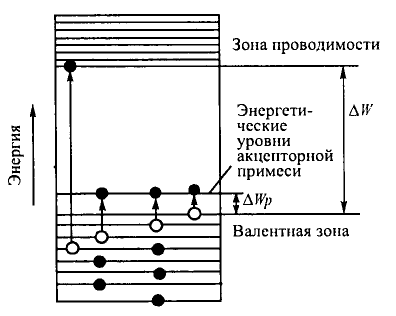
Рисунок 3.8 – Энергетическая диаграмма полупроводника р-типа
В дырочном полупроводнике, так же, как и в электронном, происходит тепловая генерация с образованием пары электрон – дырка; количество таких пар также невелико.
Применительно к акцепторному полупроводнику энергия ионизации примеси ΔWp представляет собой энергию, необходимую для присоединения недостающего электрона к акцептору.
Типичными акцепторами, кроме индия, являются бор и галлий.
Распределение электронов по энергетическим уровням для примесных полупроводников показано на рисунке 3.9.
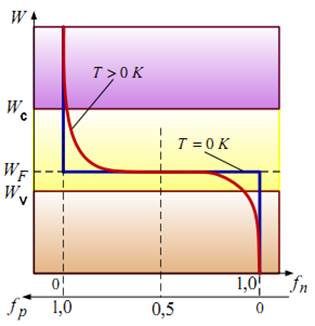 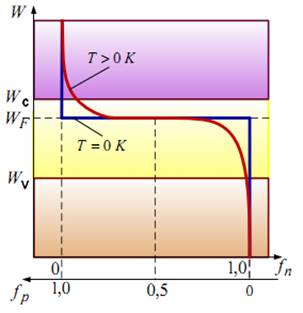
Рисунок 3.9 – Энергетические уровни для примесных полупроводников:
а – р-типа; б – n-типа
Уровни Ферми определяются для примесных полупроводников по формулам:
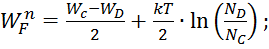
|
(3.20)
|
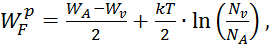
|
(3.21)
|
где ND, NA – концентрации доноров и акцепторов.
Для примесного полупроводника n-типа справедливо соотношение:
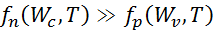 , ,
|
(3.22)
|
а для р-типа:
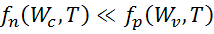 . .
|
(3.23)
|
В целом примесные полупроводники можно охарактеризовать следующим образом. Атомы примесей создают в запрещенной зоне полупроводника дополнительные примесные энергетические уровни. Эти примеси могут либо поставлять электроны в зону проводимости, либо принимать их с уровней валентной зоны. Примесная электропроводность требует для своего появления гораздо меньшей энергии (сотые и десятые доли электрон-вольта), чем для собственной электропроводности, соответственно она обнаруживается при более низких температурах. Проявление собственной электропроводности зависит от ширины запрещенной зоны: чем она шире, тем при большей температуре это происходит.
При изменении концентрации примесей в полупроводнике изменяется концентрация носителей заряда обоих знаков. Однако произведение концентраций электронов и дырок в невырожденном полупроводнике при определенной температуре в условиях термодинамического равновесия есть величина постоянная, не зависящая от содержания примесей:
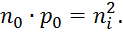
|
(3.24)
|
Это выражение называется соотношением, или законом действующих масс. Оно позволяет всегда найти концентрацию неосновных носителей заряда по известной концентрации основных. С физической точки зрения этот закон объясняется следующим образом. Если, например в полупроводнике n-типа увеличить концентрацию доноров, то возрастет количество электронов, переходящих в единицу времени с примесных уровней в зону проводимости. Соответственно возрастет скорость рекомбинации носителей заряда и уменьшится равновесная концентрация дырок.
Примесные полупроводники в целом являются электронейтральными:
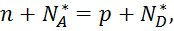
|
(3.25)
|
где NA*, ND* – концентрации ионизированных акцепторных и донорных примесей.
В полупроводниковых устройствах используется именно примесная электропроводность, т.к. появление большого количества неосновных носителей заряда в результате проявления собственной электропроводности нарушает их нормальную работу. Поэтому рабочая температура полупроводника устанавливается такой, чтобы тепловая генерация неосновных носителей заряда не сказывалась на работе устройств из него. Так, например, допустимая рабочая температура у германия составляет
+ 70oС, у кремния - от 120 до 200oС в зависимости от степени очистки.
Существуют полупроводники, которые одновременно содержат и донорные, и акцепторные примеси. Они называются компенсированными. В таких полупроводниках, несмотря на большую концентрацию примесей, уровень Ферми остаётся внутри запрещённой зоны и вырождения не наблюдается.
В компенсированных полупроводниках электроны донорной примеси, стремясь занять состояния с минимальной энергией, будут переходить на акцепторные уровни, ионизируя акцепторы. Тип проводимости при этом будет определяться разностью концентраций доноров ND и акцепторов NA. Если ND > NA, то полупроводник n-типа, а если ND < NA, то p-типа. При равенстве концентраций
ND = NA полупроводник называется полностью скомпенсированным. В этом случае проводимость в полупроводнике будет обусловлена собственными носителями заряда, однако из-за большого количества ионов примесей электропроводность такого полупроводника будет существенно ниже, чем собственного.
При малой концентрации примесей (1021...1023 м-3) примесные атомы создают дополнительные дискретные энергетические уровни в запрещенной зоне полупроводника, поэтому такие полупроводники являются невырожденными. Повышение концентрации примесных атомов в полупроводнике до 1024...1025 м-3 сопровождается появлением в запрещенной зоне полупроводника вместо дискретных уровней зон примесных уровней. Такие полупроводники относятся к вырожденным.
3. Процессы переноса зарядов в полупроводниках.
В полупроводниках процесс переноса зарядов может наблюдаться при наличии электронов в зоне проводимости и при неполном заполнении электронами валентной зоны. При выполнении этих условий и при отсутствии градиента температуры перенос носителей возможен либо под действием электрического поля, либо под действием градиента концентрации носителей заряда. В первом случае направленное движение носителей называется дрейфом, а во втором – диффузией. Дрейф носителей уже был рассмотрен (формулы (3.4) – (3.11)), поэтому остановимся на втором возможном процессе переноса зарядов.
При нормальных условиях энергия, необходимая для образования носителей заряда, приобретается за счет тепловых колебаний атомов. Обмениваясь энергией при своем взаимодействии с решеткой в процессе движения, носители заряда находятся в тепловом равновесии с ней. Именно поэтому они называются равновесными (n0, p0).
Свободные носители заряда могут также появиться под действием внешней энергии. Например, под воздействием освещения в локальном объеме полупроводника возникают избыточные (по сравнению с равновесными) носители заряда Δn, которые в момент генерации не находятся в тепловом равновесии с решеткой и поэтому называются неравновесными. За счет их появления распределение концентрации носителей заряда в объеме полупроводника становится неравномерным и при отсутствии градиента температуры в нем происходит диффузия – движение носителей заряда из-за градиента концентрации за счет собственного теплового хаотического движения. Фактически это означает выравнивание концентрации носителей заряда по всему объему. Плотность Фm потока частиц при диффузии (число частиц, пересекающих в единицу времени единичную площадку, перпендикулярную направлению градиента концентрации) пропорциональна градиенту концентрации grad(m) этих частиц:
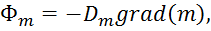
|
(3.26)
|
где Dm – коэффициент диффузии.
Различные знаки левой и правой частей выражения (3.22) объясняются тем, что вектор градиента концентрации направлен в сторону возрастания аргумента, а частицы диффундируют туда, где их меньше, т.е. против градиента концентрации.
Поскольку любое направленное движение одноименно заряженных частиц есть электрический ток, то, умножив плотность потока частиц на заряд электрона е, получают плотность электронной составляющей диффузионного тока. Электроны имеют отрицательный заряд, соответственно направление вектора диффузионного тока будет совпадать с направлением вектора градиента концентраций:
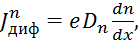
|
(3.27)
|
где 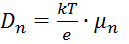 – коэффициент диффузии электронов; – коэффициент диффузии электронов;
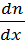 – градиент концентрации электронов. – градиент концентрации электронов.
Заряд дырок положителен, поэтому направление вектора плотности диффузионного тока дырок должно совпадать с направлением их диффузии, т.е. противоположно электронной составляющей диффузии:
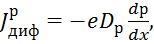
|
(3.28)
|
где 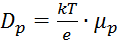 – коэффициент диффузии дырок; – коэффициент диффузии дырок;
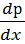 – градиент концентрации дырок. – градиент концентрации дырок.
Полная плотность диффузионного тока:
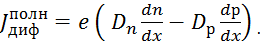
|
(3.29)
|
Одновременно с процессом диффузии носителей происходит процесс их рекомбинации, поэтому избыточная концентрация уменьшается в направлении от места образования неравновесных носителей заряда. Это изменение концентрации Δn(x) вдоль полупроводника при удалении на расстояние х от места их генерации (х = 0) описывается выражением
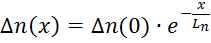 . .
|
(3.30)
|
Выражение для изменения концентрации дырок имеет аналогичный вид.
РасстояниеL, на котором в процессе диффузии в полупроводнике без электрического поля в нем избыточная концентрация носителей заряда уменьшается в результате рекомбинации в е раз, называется диффузионной длиной. Физический смысл этого понятия – это расстояние, на которое диффундирует носитель заряда за время жизни τ. Эти параметры связаны между собой соотношениями:
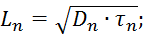
|
(3.31)
|
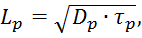
|
(3.32)
|
где τn, τp – время жизни электронов и дырок.
4. Список литературы.
1. Горелик С. С., Дашевcкий М. Я., Материаловедение полупроводников и диэлектриков, М., 1988.
2. *Мильвидский М. Г., Полупроводниковые материалы в современной электронике, М., 1986.
3. *Пасынков В. В., Сорокин В. С, Материалы электронной техники, 2 изд., М., 1986.
4. *Нашельский А. Я., Технология полупроводниковых материалов, М., 1987.
5. *Мейлихов Е. 3., Лазарев С. Д., Электрофизические свойства полупроводников. (Справочник физических величин), М., 1987.
|
|
 Скачать 384.32 Kb.
Скачать 384.32 Kb.