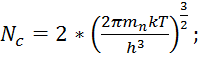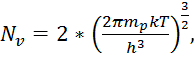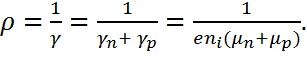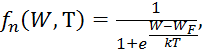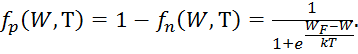|
|
Реферат. полупроводники. Электропроводность полупроводников
Реферат
на тему:
«Электропроводность полупроводников»
Группа:
Студент:Иванов И.И.
г.Екатеринбург, 2021
Содержание
Введение ……………………………………………....3
1.Собственные полупроводники……………………………………3-12
2.Примесные полупроводники………………………………..…12-22
3.Процессы переноса зарядов в полупроводниках……………………………...….22-24
4.Список литературы………………………………...24
Введение
Полупроводник - материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками и отличается от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. Основным свойством полупроводника является увеличение электрической проводимости с ростом температуры.
Полупроводниками являются вещества, ширина запрещённой зоны которых составляет порядка нескольких электрон-вольт (эВ). Например, алмаз можно отнести к широкозонным полупроводникам, а арсенид индия - к узкозонным. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и другие), огромное количество сплавов и химических соединений (арсенид галлия и др.). Почти все неорганические вещества окружающего нас мира -полупроводники. Самым распространённым в природе полупроводником является кремний, составляющий почти 30 % земной коры.
В зависимости от того, отдаёт ли примесной атом электрон или захватывает его, примесные атомы называют донорными или акцепторными. Характер примеси может меняться в зависимости от того, какой атом кристаллической решётки она замещает, в какую кристаллографическую плоскость встраивается.
Проводимость полупроводников сильно зависит от температуры. Вблизи температуры абсолютного нуля полупроводники имеют свойства диэлектриков.
1.Собственные полупроводники
Как уже отмечалось, в полупроводниках появление носителей заряда определяется рядом факторов, важнейшими из которых являются чистота материала и его температура. В зависимости от степени чистоты полупроводники делятся на собственные и примесные. Собственный полупроводник – это полупроводник, в котором отсутствуют примесные атомы другой валентности, влияющие на его электропроводность. Естественно, в реальных материалах в кристаллической решетке всегда существуют примеси, но у собственных полупроводников их концентрация пренебрежимо мала.
Рассмотрим строение полупроводникового материала, получившего наибольшее распространение в современной электронике, – кремния (Si). В кристалле этого полупроводника атомы располагаются в узлах кристаллической решетки, а электроны наружной электронной оболочки образуют устойчивые ковалентные связи, когда каждая пара валентных электронов принадлежит одновременно двум соседним атомам и крепко связана с ними. Кремний относится к IV группе таблицы Менделеева, следовательно, на наружной электронной оболочке располагаются по четыре валентных электрона; это означает, что вокруг каждого из атомов, кроме четырех собственных электронов, вращаются еще четыре соседних электрона. Таким образом, вокруг каждого атома образуются прочные электронные оболочки, состоящие из восьми обобществленных валентных электронов (рисунок 3.1). Такая связь характеризуется очень высокой прочностью.
При температуре абсолютного нуля (Т = 0 К) все энергетические состояния внутренних зон и валентная зона занята электронами полностью, а зона проводимости совершенно пуста, поэтому кристалл полупроводника фактически является диэлектриком.
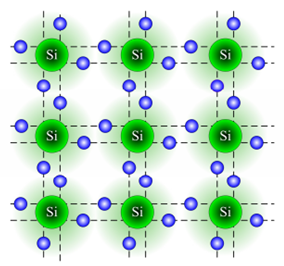
Рисунок 3.1 – Структура связей атома кремния в кристаллической решетке при Т = 0 К
При передаче кристаллической решетке дополнительной энергии, например при повышении температуры в результате поглощения каким-либо электроном этой дополнительной энергии, он разрывает ковалентную связь. Появляется вероятность его перехода в зону проводимости, где он становится свободным носителем n электрического заряда (рисунок 3.2), причем, чем больше температура, тем выше эта вероятность. Одновременно с этим у того атома полупроводника, от которого отделился электрон, возникает незаполненный энергетический уровень в валентной зоне, называемый дыркой р. Она представляет собой единичный положительный электрический заряд (равный по модулю заряду электрона) и может перемещаться по всему объему полупроводника под действием электрических полей, диффузии (в результате разности концентраций носителей заряда в различных зонах полупроводника), а также в результате теплового движения. На самом деле движутся только электроны, но их эстафетное перескакивание с атома на атом можно формально описать как движение одной дырки, перемещающийся в направлении, обратном движению электронов, т.е. в направлении поля.
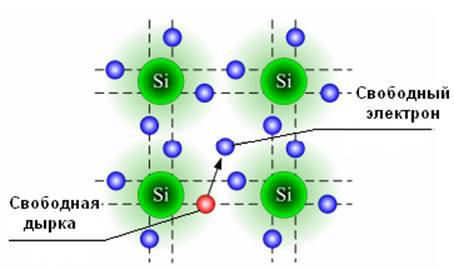
Рисунок 3.2 – Генерация пары свободных носителей заряда
«электрон – дырка» при Т > 0 К
Таким образом, в идеальном кристалле полупроводника при нагревании образуются пары носителей заряда «электрон – дырка», которые обуславливают появление собственной электрической проводимости полупроводника.
Процесс образования пары «электрон – дырка» называется генерацией свободных носителей заряда. Скорость генерации G определяется количеством пар носителей заряда, генерируемых в единицу времени. Она обратно пропорционально ширине запрещенной зоны ΔW и прямо пропорциональна температуре Т.
Эта пара существует в течение некоторого времени, называемого временем жизни носителей электрического заряда (оно обозначается τn для электронов и τp для дырок). В течение этого промежутка времени носители участвуют в тепловом движении, взаимодействуют с электромагнитными полями как единичные электрические заряды, перемещаются под действием градиента концентрации. Затем в результате хаотического движения электрона происходит восстановление ковалентной связи электрона с атомом – так называемая рекомбинация, в результате которой пара носителей заряда исчезает. Скорость рекомбинации R определяется количеством пар носителей заряда, исчезающих в единицу времени.
Для собственного полупроводника τn = τp = τi. В состоянии термодинамического равновесия (т.е. при постоянной температуре) скорости генерации и рекомбинации одинаковы, поэтому в полупроводнике устанавливаются равновесные собственная концентрация электронов ni и собственная концентрация дырок pi; т.к. они генерируются попарно, для собственного полупроводника выполняется условие ni = pi. При комнатной температуре собственная концентрация составляет, например, для кремния 1,4*1010 см-3, а для германия 2,5*1013 см-3. Она рассчитывается по формуле:
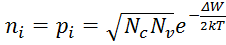 , ,
|
(3.1)
|
где ΔW – ширина запрещенной зоны, Дж;
k – постоянная Больцмана, Дж/К;
T – абсолютная температура, К;
Nc, Nv – эффективные плотности состояний в зоне проводимости и в валентной зоне соответственно, м-3.
Эффективные плотности состояний рассчитываются по формулам:
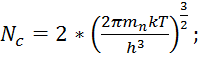
|
(3.2)
|
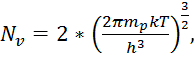
|
(3.3)
|
где mn, mp – эффективные массы электрона и дырки соответственно, кг;
h – постоянная Планка.
Физический смысл понятия «плотность энергетических состояний» – это число состояний, приходящихся на единичный интервал энергии, или плотность состояний.
Как следует из (3.1), с увеличением температуры собственные концентрации электронов и дырок растут по экспоненциальному закону.
Энергетическая диаграмма собственного полупроводника показана на рисунке 3.3. Электроны обозначены черными кружками, а дырки – белыми. Распределение электронов по уровням энергии соответствует некоторой температуре Т, при которой в зону проводимости перешло несколько электронов, образовав в валентной зоне соответствующее количество дырок.
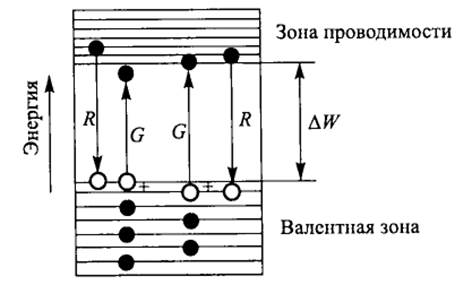
Рисунок 3.3 – Энергетическая диаграмма собственного полупроводника
Как уже отмечалось, специфика собственного полупроводника состоит в том, что равновесная концентрация электронов и дырок одинакова (ni = pi). Тогда общее число свободных носителей заряда в единице объема собственного полупроводника будет равно 2ni. Под действием внешнего электрического поля с напряженностью Е в нем возникает направленное движение этих зарядов, т.е. электрический ток. В его создании принимают участие как электроны, так и дырки. Ток, создаваемый электронами, можно найти по формуле:
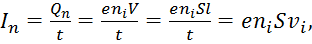
|
(3.4)
|
где Qn – суммарный заряд, переносимый электронами за время t через поперечное сечение полупроводника S, перпендикулярное направлению электрического поля;
е – заряд электрона;
ni – концентрация электронов в зоне проводимости, т.е. число электронов в единице объема;
V – объем электронов, проходящий через сечение S за время t;
l – длина объема V в направлении движения электронов;
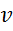 n n – средняя скорость упорядоченного движения электронов (дрейфовая скорость). – средняя скорость упорядоченного движения электронов (дрейфовая скорость).
Плотность тока Jn, создаваемая электронами, будет равна:
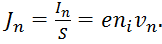
|
(3.5)
|
Средняя скорость электронов пропорциональна напряженности поля:
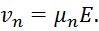
|
(3.6)
|
Коэффициент пропорциональности μn называется подвижностью электронов, он имеет размерность м2/(В*с). Физический смысл подвижности – это дрейфовая скорость, приобретаемая электроном в поле единичной напряженности.
Тогда плотность тока:
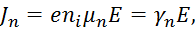
|
(3.7)
|
где 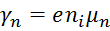 – удельная электронная проводимость собственного проводника. – удельная электронная проводимость собственного проводника.
Аналогично для дырочной проводимости:
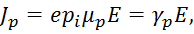
|
(3.8)
|
где 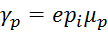 – удельная дырочная проводимость собственного проводника; – удельная дырочная проводимость собственного проводника;
pi – концентрация дырок в валентной зоне;
μp – подвижность дырок.
Учитывая, что в собственном полупроводнике электрический ток обусловлен движением как электронов, так и дырок, суммарная плотность тока:
Тогда удельная проводимость собственного полупроводника:
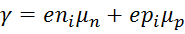 = =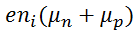 , ,
|
(3.10)
|
а удельное сопротивление будет равно:
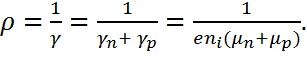
|
(3.11)
|
Таким образом, при любой температуре материала в состоянии термодинамического равновесия устанавливается равновесная концентрация возбужденных носителей заряда:
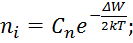
|
(3.12)
|
где ΔW – ширина запрещенной зоны полупроводника;
Cn, Cp – постоянные величины для концентрации электронов в зоне проводимости и дырок в валентной зоне.
Коэффициент, равный 2, в знаменателе показателя экспоненты объясняется следующим соображением. В собственном полупроводнике для перехода электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачивается энергия активации, равная ширине запрещенной зоны ΔW. При появлении электрона в зоне проводимости в валентной зоне обязательно появляется дырка, т.е. энергия ΔW затрачивается на образование пары носителей заряда.
Подвижности электронов μn и дырок μp имеют различное значение. Электроны и дырки обладают разной инерционностью при движении в поле кристаллической решетки полупроводника, т.е. отличаются друг от друга эффективными массами 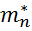 и и 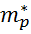 . В большинстве случаев . В большинстве случаев 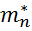 < < 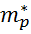 . Поэтому собственная электропроводность полупроводников имеет слабо выраженный электронный характер. . Поэтому собственная электропроводность полупроводников имеет слабо выраженный электронный характер.
Переход электрона с одного энергетического уровня на другой носит вероятностный характер, поэтому обычно оценивается вероятность нахождения электрона на каком-либо уровне W при температуре Т.
Распределение электронов по энергетическим уровням в твердом теле при некоторой постоянной температуре Т описывается статистикой Ферми-Дирака. С помощью статистики Ферми-Дирака можно определить концентрацию электронов в зоне проводимости дырок в валентной зоне и определить зависимость удельной электропроводности полупроводника от температуры, наличия примесей и других факторов.
Вероятность заполнения электроном энергетического уровня W при температуре Т определяется функцией распределения Ферми:
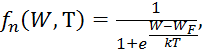
|
(3.13)
|
где Т – абсолютная температура;
k – постоянная Больцмана;
WF – энергия уровня Ферми.
Уровнем Ферми называется уровень, для которого вероятность нахождения на нем электрона равна 0,5 при любой температуре.
Если уровень W не занят электроном, значит, его занимает дырка. Поскольку сумма вероятностей нахождения на одном уровне для электрона и дырки равна 1, функция распределения Ферми для дырки может быть найдена следующим образом:
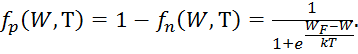
|
(3.14)
|
Как видно из последних формул, функции вероятности для электрона и дырки аналогичны. Различие состоит только в том, что для электронов энергия возрастает при движении вверх от уровня Ферми, а для дырок – наоборот, при движении вниз.
Вид функций вероятности показан на рисунке 3.4. При температуре Т=0К функция распределения Ферми имеет ступенчатый характер. Это означает, что в этом случае все энергетические уровни, находящиеся выше уровня Ферми, свободны. При увеличении температуры вероятность заполнения этих энергетических уровней также увеличивается. Поэтому характер функции распределения становится более плавным в сравнительно узкой области энергий, близких к WF.
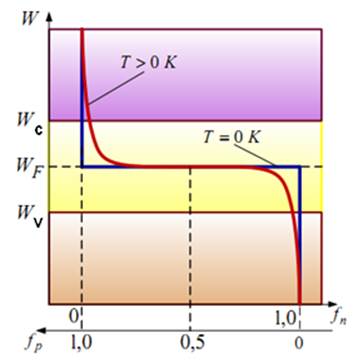
Рисунок 3.4 – Распределение электронов по энергетическим уровня для собственного полупроводника
Обычно в полупроводниках разность энергий W – WF достаточно велика и превышает значение 3kT. Это позволяет пренебречь единицей в знаменателях выражений (3.13) и (3.14) и перейти к статистике Максвелла-Больцмана:
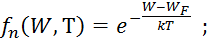
|
(3.15)
|
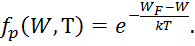
|
(3.16)
|
Эта статистика используется для невырожденных полупроводников, т.е. таких, у которых уровень Ферми расположен в запрещенной зоне на достаточном удалении от границ валентной зоны и зоны проводимости. Собственные полупроводники в нормальных условиях являются невырожденными. Положение уровня Ферми в собственных полупроводниках находится по формуле:
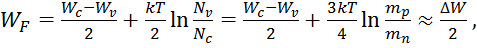
|
(3.17)
|
т. е. он расположен примерно посередине запрещенной зоны. Он одинаков во всех частях равновесной системы, какой бы разнородной она не была.
Вырожденный полупроводник – это полупроводник, концентрация примесей в котором настолько велика, что собственные свойства практически не проявляются, а проявляются в основном свойства примеси. У вырожденного полупроводника уровень Ферми лежит внутри разрешённых зон или внутри запрещённой зоны на расстояниях не более kT от границ разрешённых зон. Вырожденные полупроводники получают путём сильного легирования собственных полупроводников. Для описания распределения носителей заряда в вырожденных полупроводниках применяется статистика Ферми-Дирака. Кроме высокой степени легирования (легированием называется введение примесей в полупроводник), причиной вырождения может быть высокая температура или малая ширина запрещенной зоны.
Число электронов в зоне проводимости и дырок в валентной зоне можно найти как произведение плотности уровней в зоне проводимости на вероятность их заполнения электронами (для дырок это будет произведение плотности уровней в валентной зоне на вероятность появления там дырок). Тогда равновесные концентрации электронов n0 и р0 в собственном полупроводнике будут равны:

|
(3.18)
|
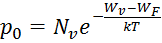 . .
|
(3.19)
|
| |
|
|
 Скачать 384.32 Kb.
Скачать 384.32 Kb.