Обработка (1). Электростатическое поле коаксиального кабеля
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Теоретических Основ Электротехники отчет по лабораторной работе №1 по дисциплине «Теоретические Основы Электротехники» Тема: Электростатическое поле коаксиального кабеля
Санкт-Петербург 2019 Цель работы: Изучение влияния конструктивных параметров коаксиального кабеля на картину электростатического поля во внутренней области. Одножильный кабель на рабочее 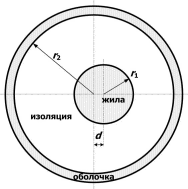 напряжение U0 имеет радиус жилы r1 и внутренний радиус оболочки r2 (рис.1). напряжение U0 имеет радиус жилы r1 и внутренний радиус оболочки r2 (рис.1).В идеале оба проводника должны иметь общую ось, однако в процессе изготовления или эксплуатации возможно смещение проводников на расстояние d, что может привести к пробою изоляции кабеля, если максимальная напряженность электростатического поля превысит допустимое значение. Рис.1 Конструкция коаксиального кабеля Обычно при проектировании коаксиального кабеля задается радиус жилы r1, который выбирается по величине токовой нагрузки. Внешний радиус изоляции (внутренний радиус оболочки r2 ) определяется исходя из допустимого значения максимальной напряженности электростатического поля и рабочего напряжения кабеля: 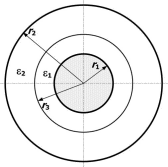 Для кабеля с двухслойной изоляцией (рис.2) оптимальное распределение напряженности поля достигается при соблюдении равенства: Для кабеля с двухслойной изоляцией (рис.2) оптимальное распределение напряженности поля достигается при соблюдении равенства:Радиус оболочки r2 в этом случае может быть найден из равенства: 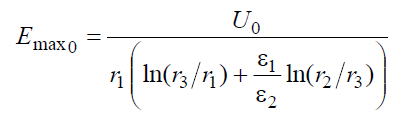 Рис.2 Кабель с градированной изоляцией При расчете электростатического поля, создаваемое такой системой проводников, принимают, что потенциал на поверхности внутреннего проводника (жилы) равен U0, а потенциал на поверхности наружного проводника равен нулю. При этом поле сосредоточено в области диэлектрика, заполняющего кабель, и во внешнее пространство не проникает. Здесь учитывается и тот факт, что электростатическое поле в проводник не проникает, поэтому поверхности проводников становятся границами области существования поля. Задача № 1: Определить, на какую величину может быть допущено смещение оси жилы кабеля по отношению к оси оболочки, чтобы максимальная напряженность поля в диэлектрике не превысила двойной по сравнению с максимальной напряженностью при совпадении осей. Изоляцию кабеля считать однородной. Построить зависимость Emax(d) (результаты расчета Emax для различных d должны быть занесены в таблицу). Для построения использовать не менее 810 точек. Привести зависимости напряженности поля вдоль контура a b для исходной и конечной конфигурации. Привести картину эквипотенциальных линий для конечной модели. Дано: 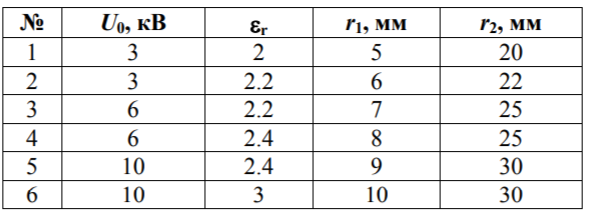 Для несмещенного кабеля: 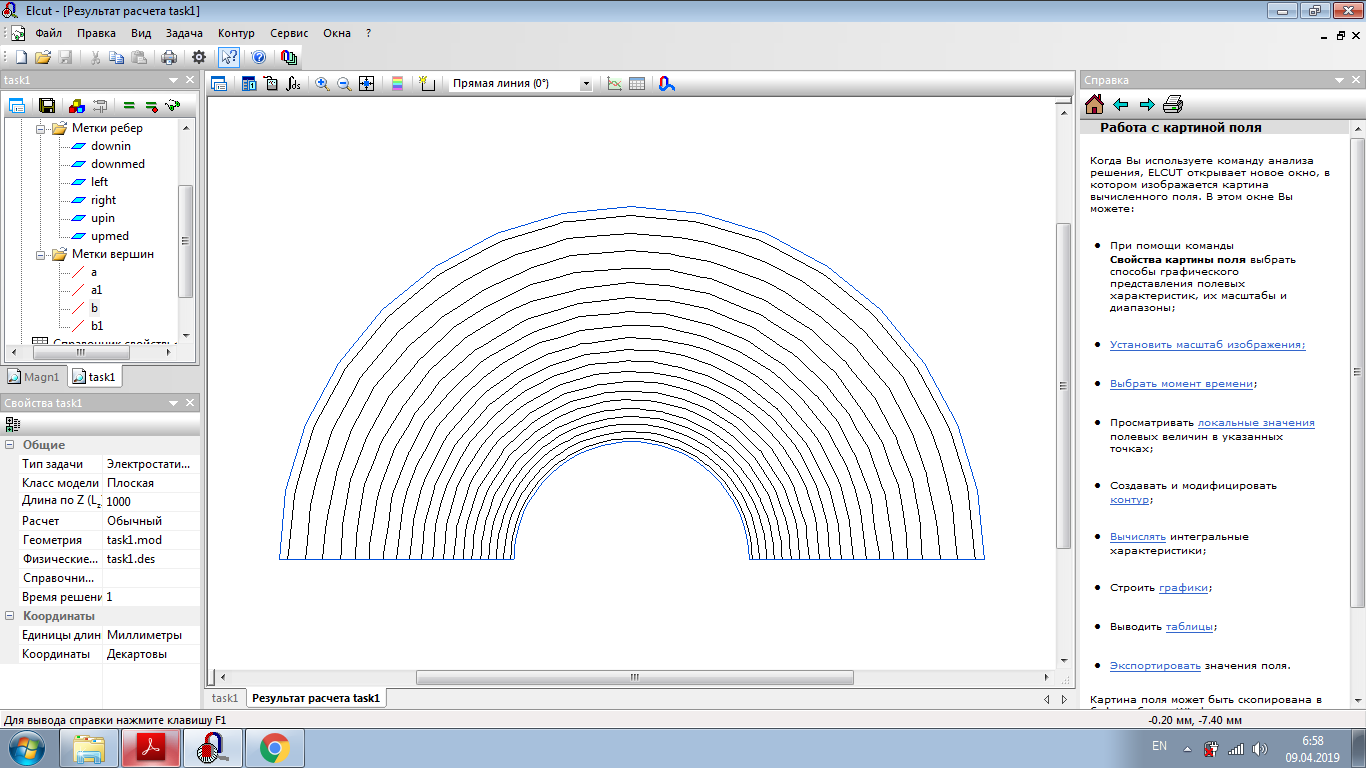 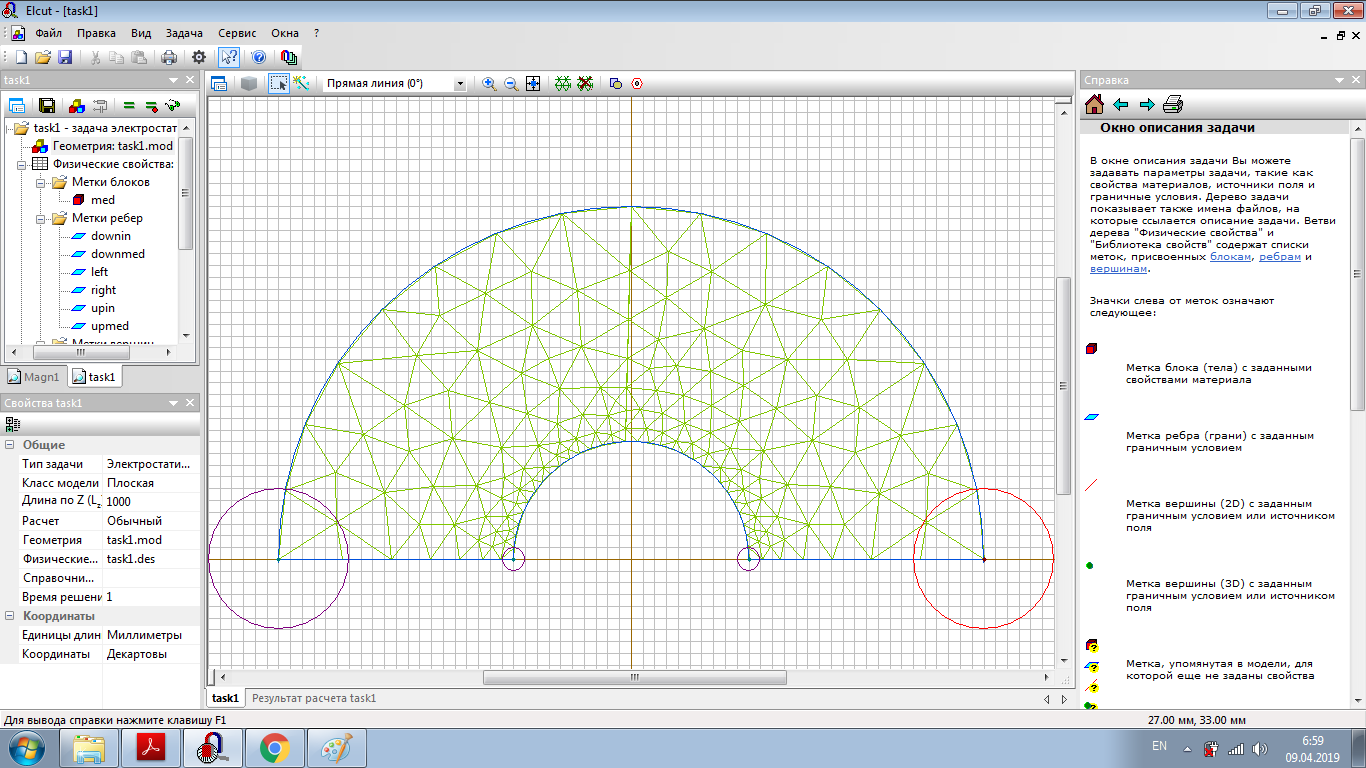  Картина эквипотенциальных линий  Исходная конфигурация 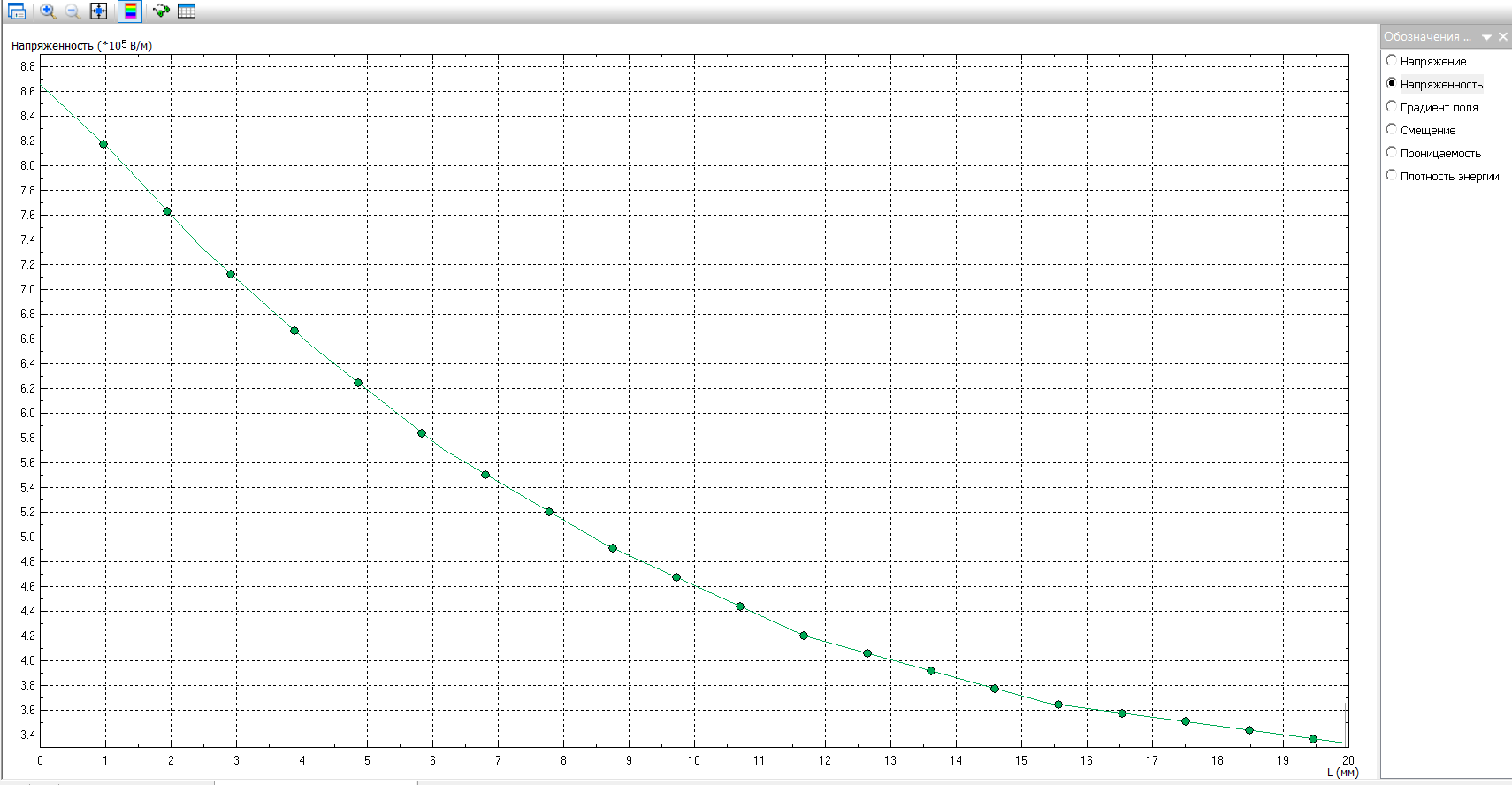  Напряженность поля вдоль контура
 Emax(d), В/м  d,мм 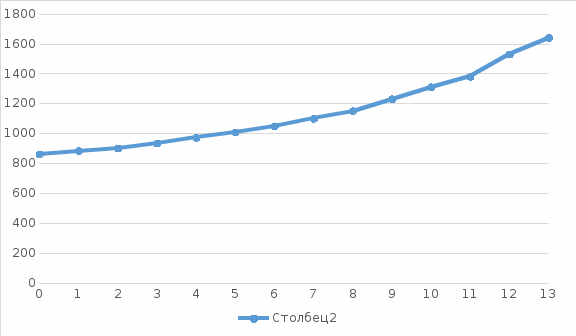 Для кабеля, смещенного на 13 мм: 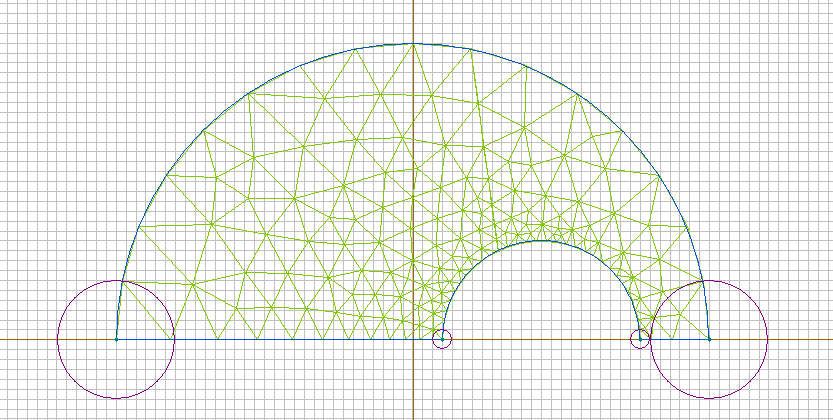 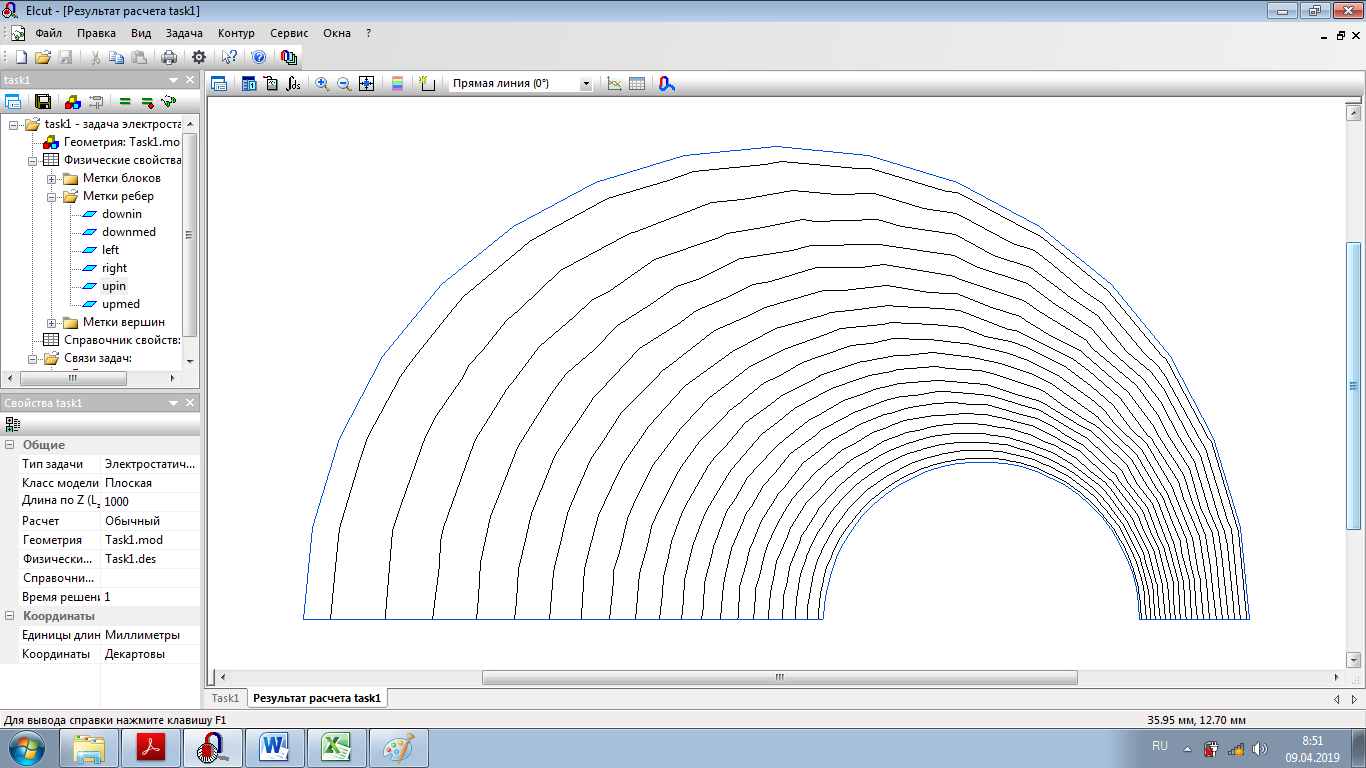   Картина эквипотенциальных линий для конечной конфигурации Конечная конфигурация  Напряженность поля вдоль контура для конечной конфигурации 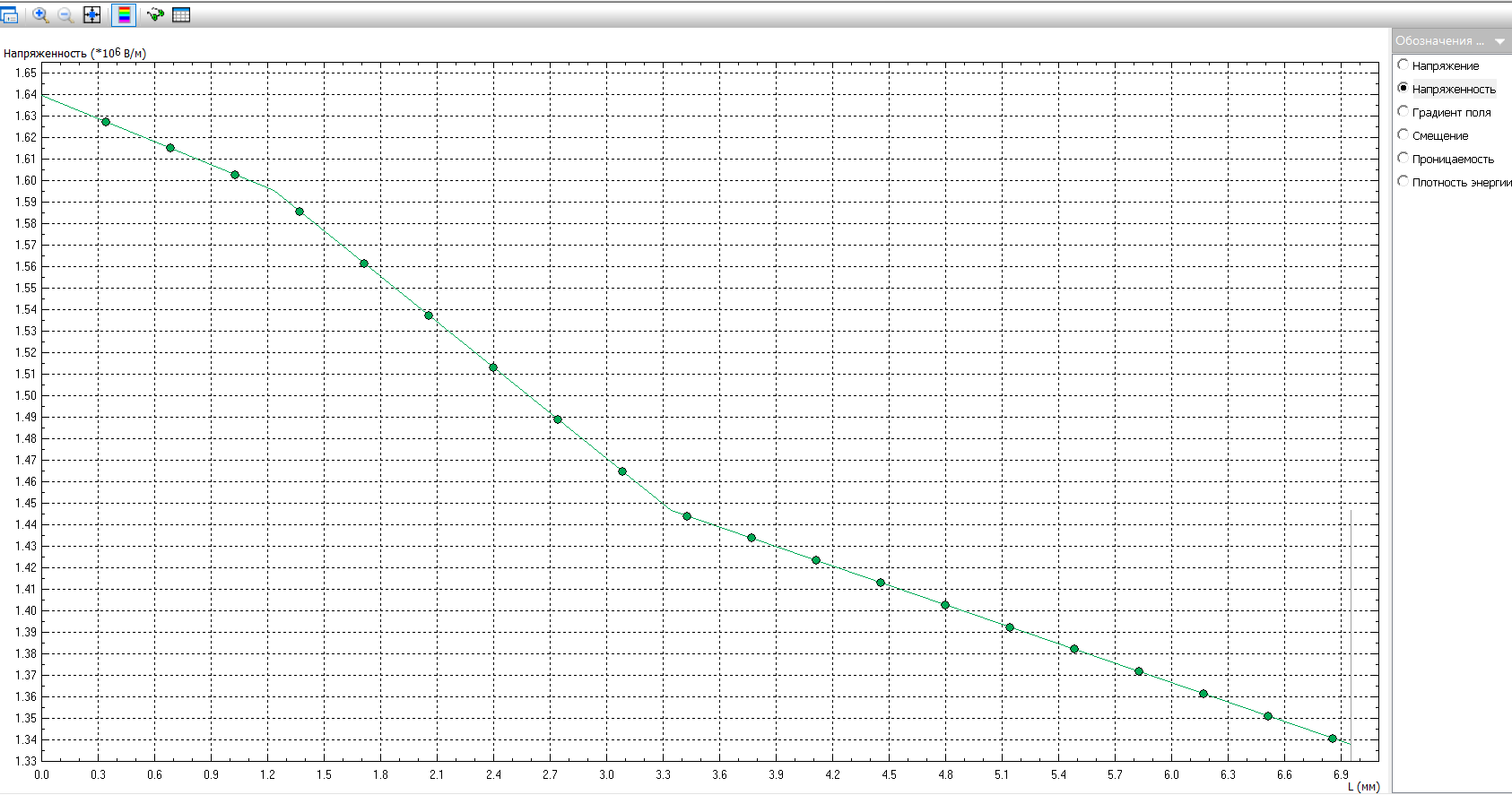 Задача № 2: При заданном размере оболочки кабеля, рассчитанного на U0 = 3 кВ, определить оптимальный радиус жилы (соответствует минимальному значению максимальной напряженности поля в конструкции). Результирующее значение найти с точностью до десятых долей миллиметра. Исходное значение радиуса жилы приведено в таблице. Построить зависимость Emax(r1) (результаты расчета Emax для различных r1 должны быть занесены в таблицу). Для построения использовать не менее 810 точек. Привести зависимости напряженности поля вдоль контура a b для исходной и оптимальной конструкции и картину эквипотенциальных линий для оптимальной модели.   Картина эквипотенциальных линий Исходная конфигурация Д 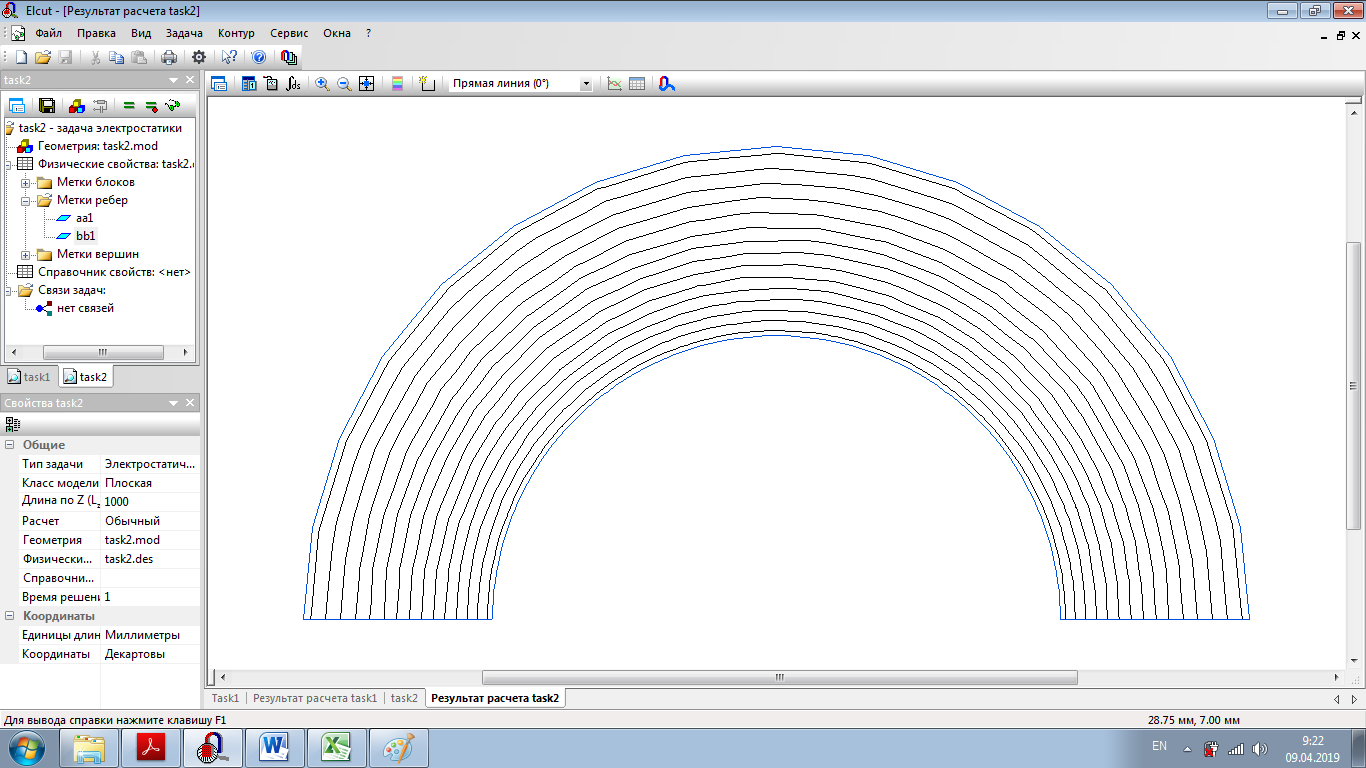 ано: ано: 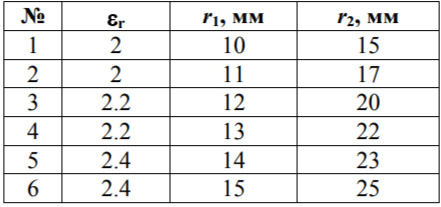 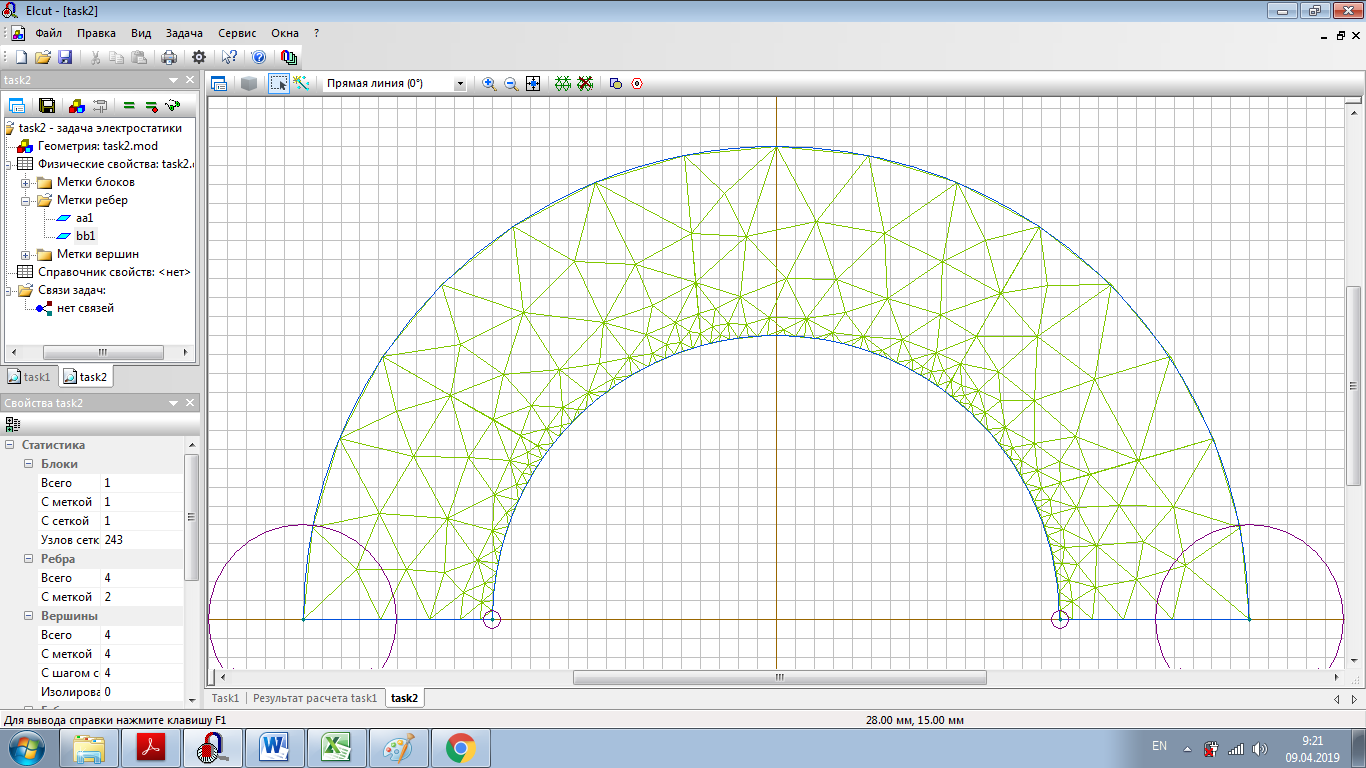  Напряженность поля вдоль контура для исходной конфигурации 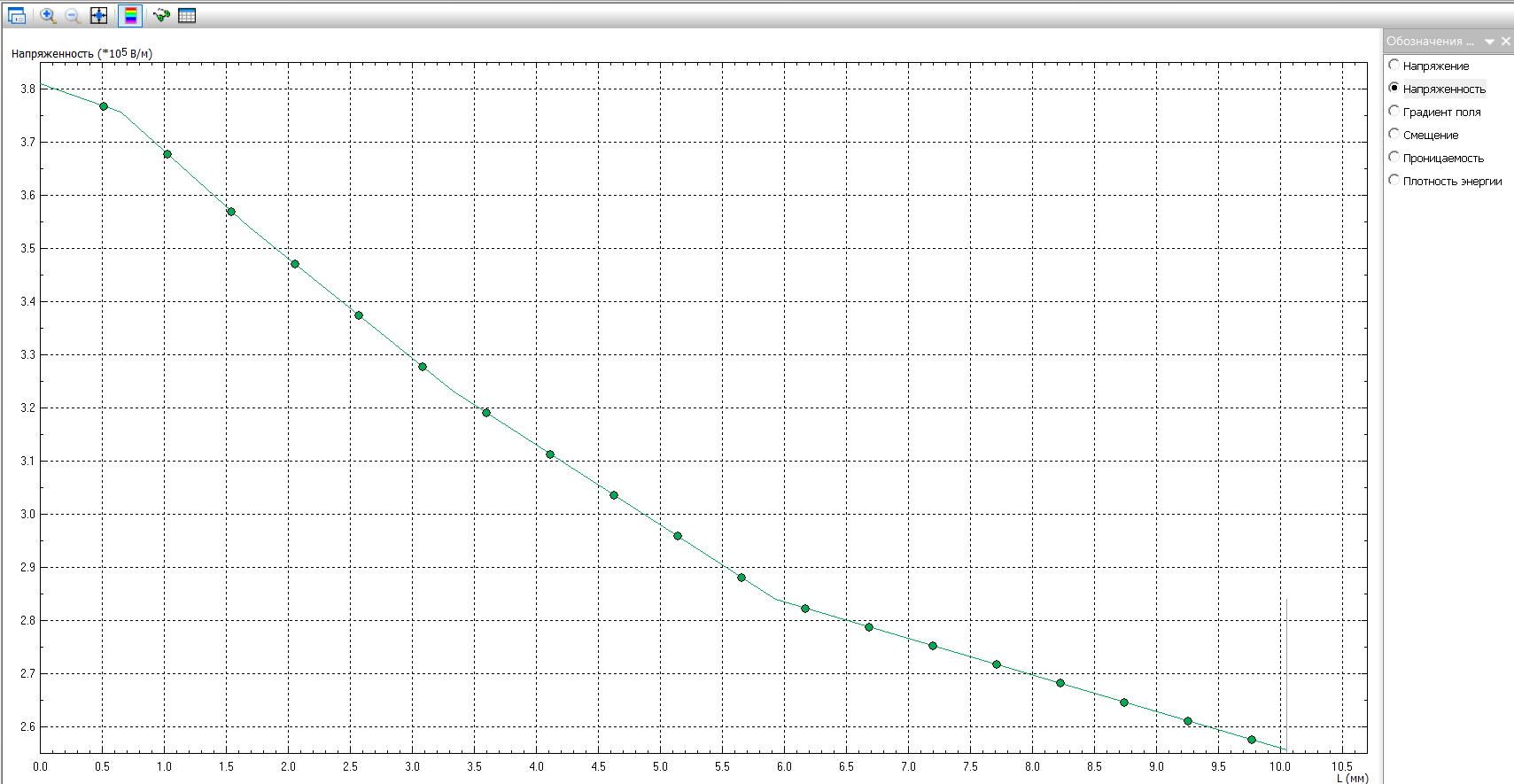 Таблица 2
Зависимость напряженности от радиуса жилы: 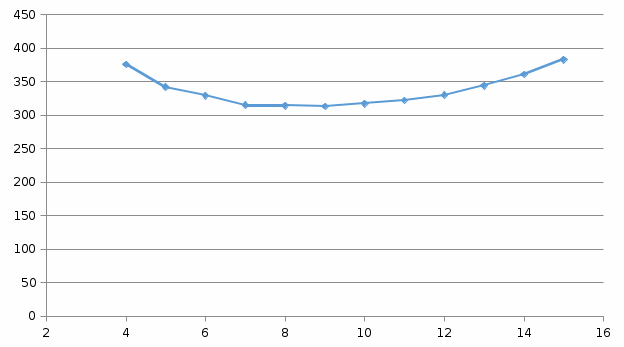 По таблице 2 можно сделать вывод, что искомый радиус находится в диапазоне от 8 до 9мм. Определим эти значения более точно:
Наименьшее значение максимальной напряженности наблюдается при радиусе: r1 = 8,2 мм Для оптимальной конструкции: 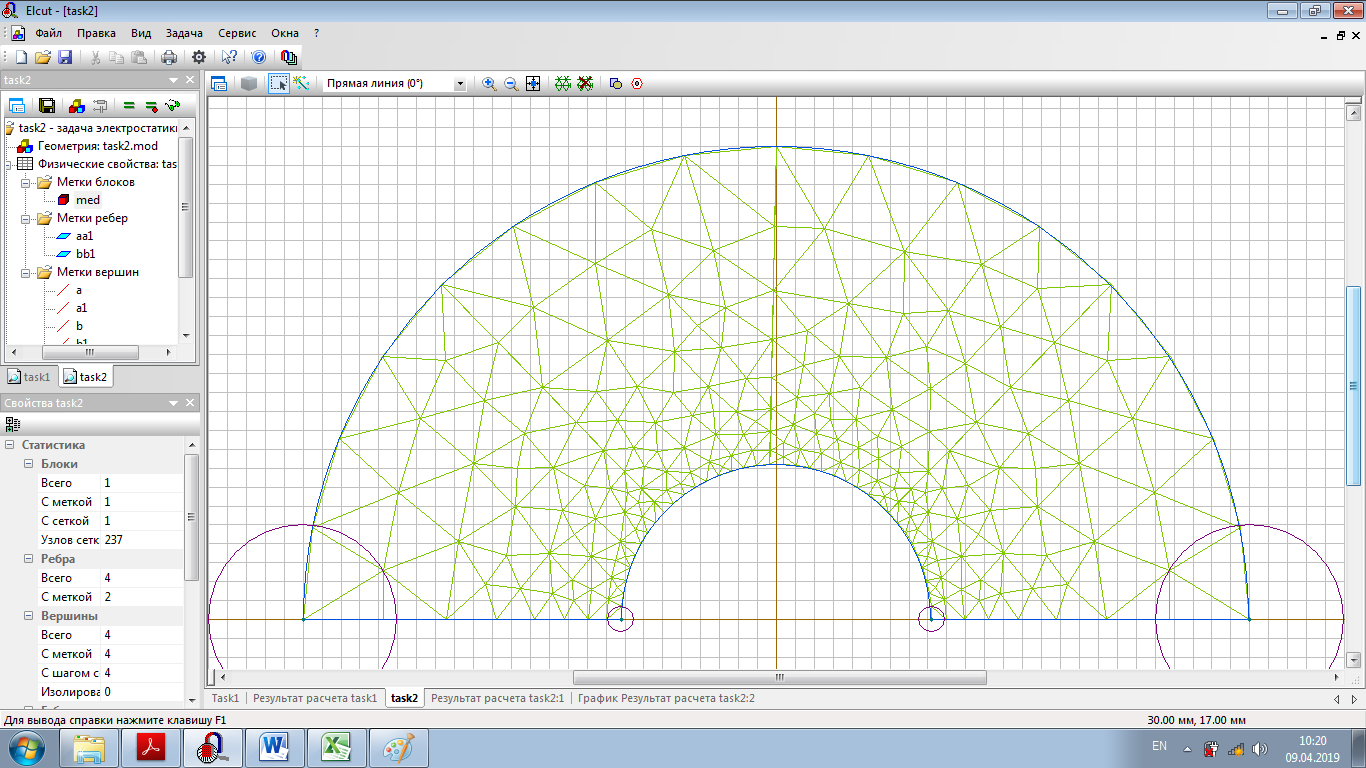 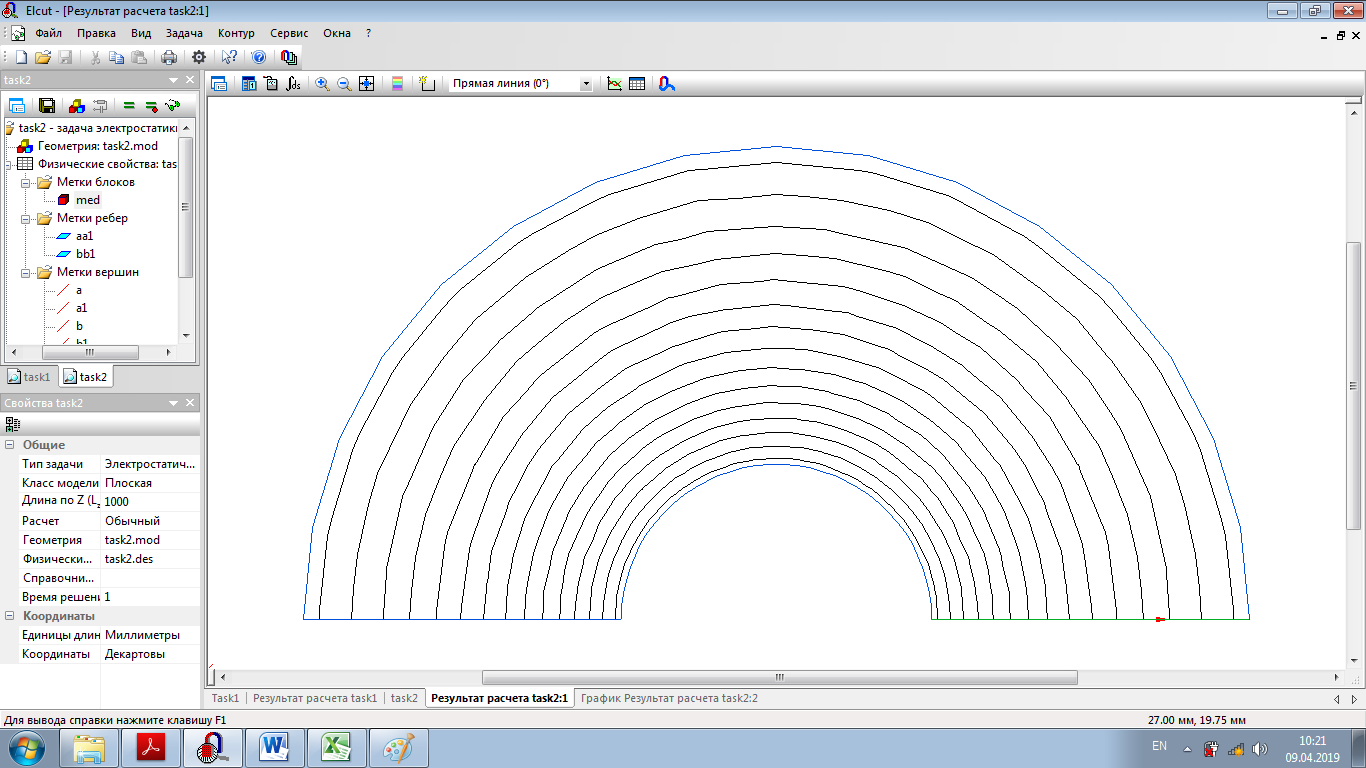    Напряженность поля вдоль контура для оптимальной конфигурации Картина эквипотенциальных линий для оптимальной конфигурации Оптимальная конфигурация 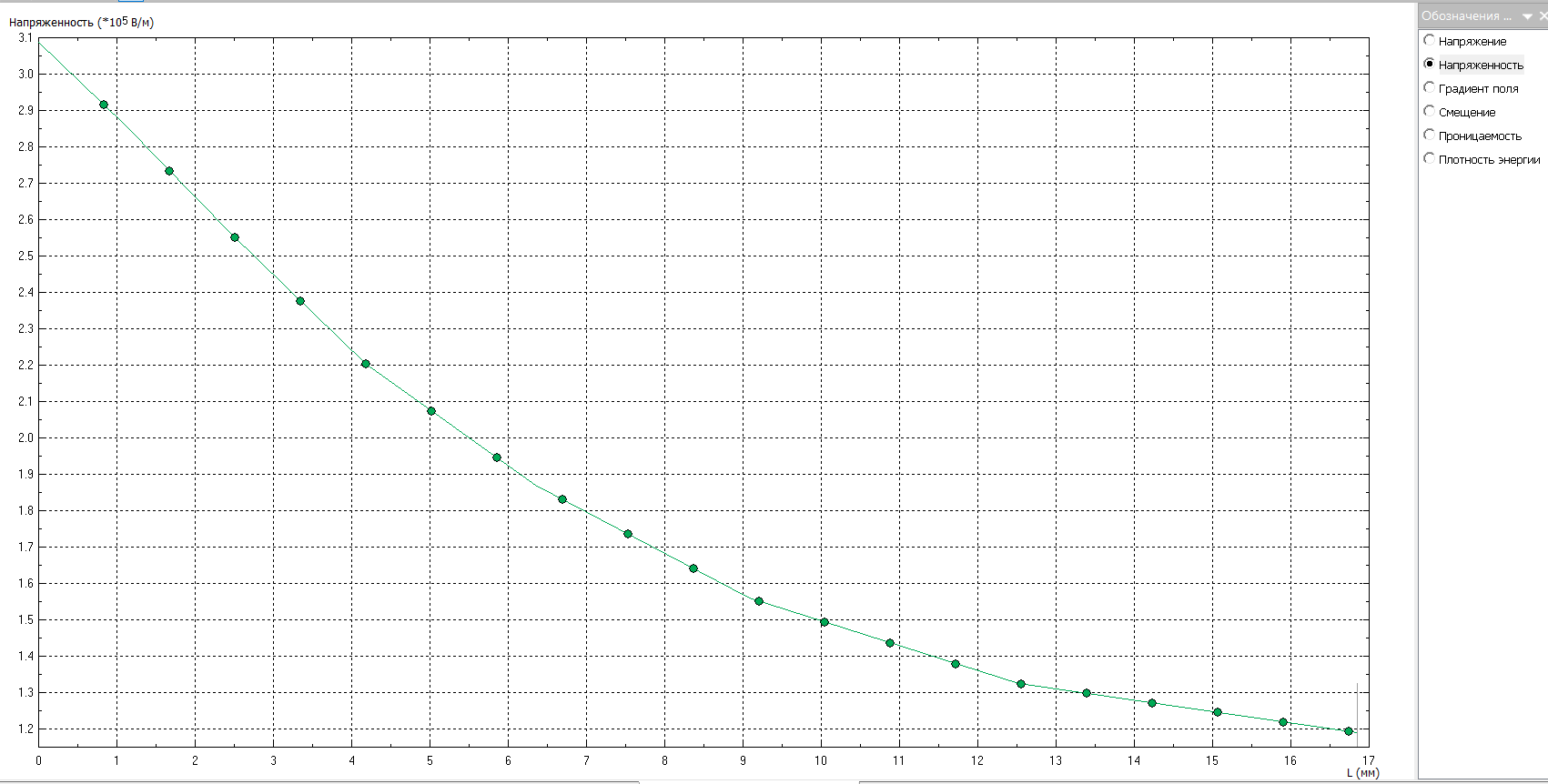 Задача № 3: Исследовать, как изменится радиус оболочки кабеля при использовании двухслойного диэлектрика. Вначале по формуле (2) рассчитать радиус внутреннего слоя изоляции (r3), а потом изменять радиус оболочки так, чтобы напряженность не превысила Emax0 = 2.5⋅106 В/м. Базовый вариант – кабель с однородной изоляцией r2. Построить зависимость Emax(r2) (результаты расчета Emax для различных r2 должны быть занесены в таблицу). Для построения использовать не менее 68 точек. Привести зависимости напряженности поля вдоль контура a b для базового и оптимального варианта и картину эквипотенциальных линий для оптимальной модели. Дано: 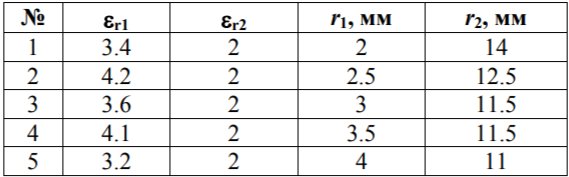 Рассчитаем оптимальное значение внутреннего слоя изоляции: 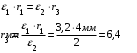 Для базового варианта с диэлектрической проницаемостью 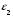 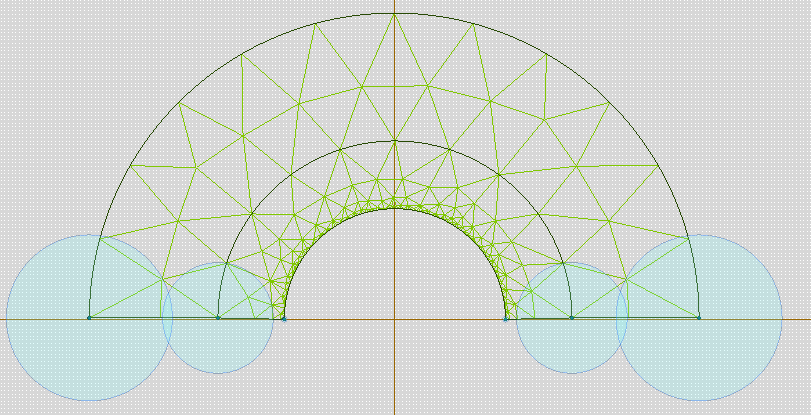 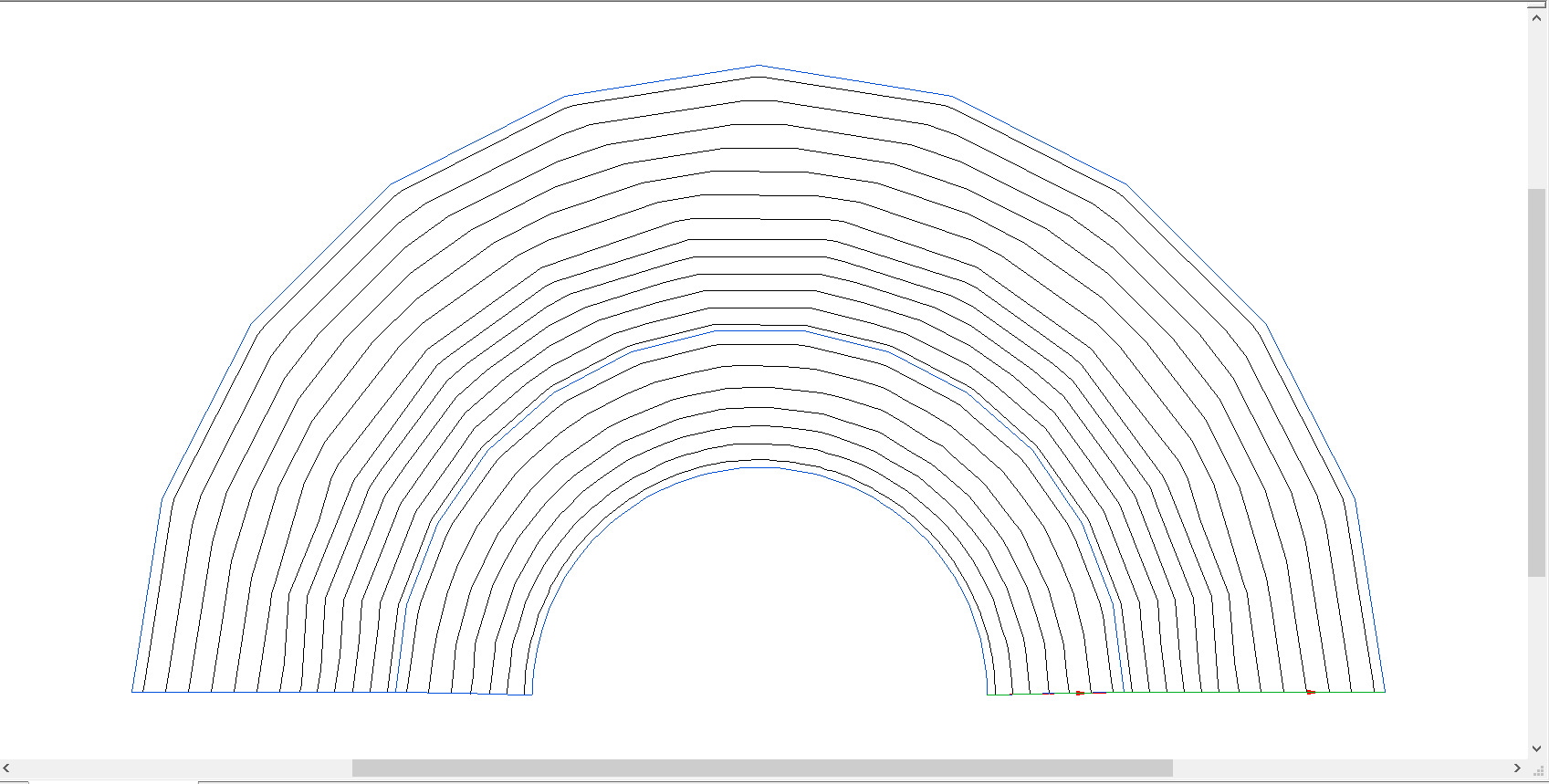 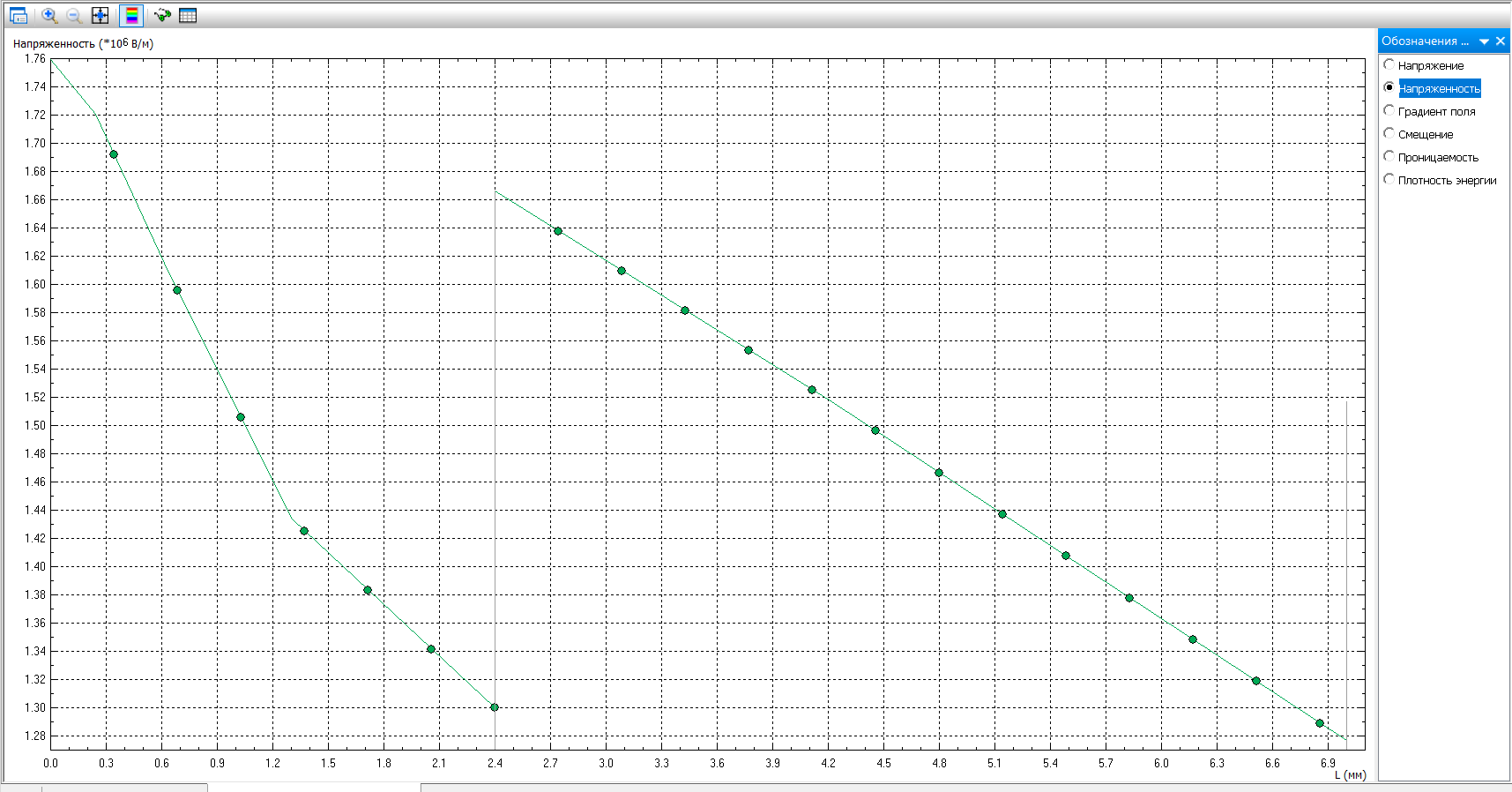 Зависимость напряженности (в МВ/м) от радиуса внешней оболочки) 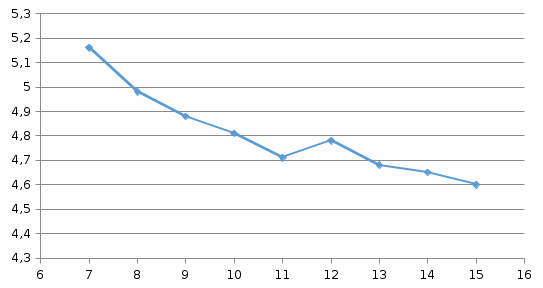
Выводы: С помощью программного пакета Elcut были рассчитаны характеристики провода, оптимальные значения параметров: Для коаксиального кабеля заданных параметров получили максимальное допустимое смещение, при котором максимальная напряженность не превышает двойной напряженности на кабеле с несмещенной жилой: d= 13мм, E(d)=1730 В\м Для коаксиального кабеля заданных параметров получили значение радиуса жилы, при которой наблюдается наименьший максимум напряженности: r1=8.2 мм |
