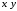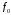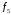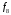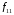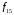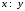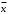Дискретная математика лекция 1. Элементы математической логики высказывания. Логические операции (алгебра Буля). Определение
 Скачать 232.49 Kb. Скачать 232.49 Kb.
|
|
Лекция 1 Дискретная математика В этом курсе лекций мы коснёмся трёх разделов дискретной математики: математическая логика, теория графов и теории множеств. Глава 1. Элементы математической логики §1. Высказывания. Логические операции (алгебра Буля). Определение. Высказыванием в математической логике называется повествовательное предложение, утверждающее что-либо, о котором можно сказать, истинно оно или ложно при данных условиях. Примеры: три больше одного – высказывание истинно; Волга впадает в Каспийское море – высказывание истинно; все нечётные натуральные числа простые – высказывание ложно; в следующий четверг пойдёт дождь – не является высказыванием. В математической логике не интересуются содержанием высказывания, а только его истинностью. Поэтому, обозначая высказывания буквами  , ,  , и т.д., мы будем рассматривать их как логические переменные, принимающие два значения: 0 если высказывание ложно; 1 если высказывание истинно. С этой точки зрения полезно ввести логические постоянные: 1 – высказывание, которое истинно при любых условиях. 0 – высказывание, которое ложно при любых условиях. , и т.д., мы будем рассматривать их как логические переменные, принимающие два значения: 0 если высказывание ложно; 1 если высказывание истинно. С этой точки зрения полезно ввести логические постоянные: 1 – высказывание, которое истинно при любых условиях. 0 – высказывание, которое ложно при любых условиях.Определение. Высказывания  и и  называются эквивалентными, если они истинны или ложны одновременно. называются эквивалентными, если они истинны или ложны одновременно.Факт эквивалентности записывается в виде 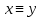 или или  . .Определение. Логической (булевой) функцией от  логических переменных логических переменных 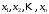 называется функция называется функция 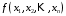 , принимающая значения из множества , принимающая значения из множества  . .Замечание. Другими словами, функция 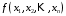 называется логической, если она сама и все её переменные принимают только два значения 0 и 1. называется логической, если она сама и все её переменные принимают только два значения 0 и 1. Определение. Логические функции 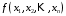 и и 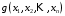 называются равносильными или равными, если они принимают одинаковые значения на всех всевозможных наборах значений переменных называются равносильными или равными, если они принимают одинаковые значения на всех всевозможных наборах значений переменных 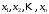 . .Часто логическую функцию задают таблично, т.е. в левом столбце выписывают всевозможные значения аргументов, а в правом столбце – соответствующие значения функции. В математической логике такое табличное задание функции называется таблицей истинности функции. Более подробно о таблицах истинностей логических функций поговорим в следующем параграфе. Рассмотрим важные в дальнейшем четыре логические функции (операции). 1. Отрицание высказывания  . .Отрицание высказывания  истинно если истинно если  ложно, и ложно если ложно, и ложно если  истинно. истинно. Эта функция (операция) обозначается  и читается “не и читается “не  ”. ”. Таблица истинности для этой функции одной переменной имеет вид
2. Конъюнкция высказываний  и и  . . Конъюнкция высказываний истинна если оба высказывания  и и  истинны и ложна в других случаях. Эта функция (операция) обозначается  или или 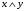 и читается “ и читается “ и и  ”. ”. Таблица истинности для этой функции двух переменных имеет вид
3. Дизъюнкция высказываний  и и  . . Дизъюнкция высказываний ложна если оба высказывания  и и  ложны и истинна в других случаях. Эта функция (операция) обозначается  и читается “ и читается “ или или  ”. ”. Таблица истинности для этой функции двух переменных имеет вид
4. Импликация (от лат. implicatio — «связь»). Импликация “если  , то , то  ” ложна если высказывание ” ложна если высказывание  истинно, высказывание истинно, высказывание  ложно, в других случаях импликация истинна. ложно, в других случаях импликация истинна.Эта функция (операция) обозначается 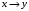 и читается “если и читается “если  , то , то  ”. ”. Таблица истинности для этой функции двух переменных имеет вид
Замечание. Если последние две строки в этой таблице не вызывают интуитивного непонимания, то вторая и третья строчки, возможно, вызывают это непонимание. Для прояснения этой функции рассмотрим два примера высказываний. Пример для второй строки. “Если число делится на 5, то его квадрат делится на 5.” Это истинное высказывание. Поэтому высказывание: “Если 7 делится на 5, то его квадрат 49 делится на 5” – истинно. Пример для третьей строки. “Если одно слагаемое делится на 5 и второе слагаемое делится на 5, то сумма этих чисел делится на 5.” Это истинное высказывание. Поэтому высказывание: “Если 12 делится на 5 и 13 делится на 5, то сумма этих чисел 25 делится на 5” – истинно. Упражнения. Доказать равенства (эквивалентности) 1.  2.  . .Напоминание (подсказка). Равенства логических функций можно доказывать, сравнивая таблицы истинности. Свойства конъюнкции, дизъюнкции и отрицания. 1. А) универсальные границы:  , , 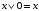 , , , , 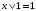 ; ;Б) идемпотентность: 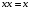 , ,  ; ;В) дополнение:  , , 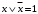 , ,  , ,  ; ;Г) инволютивность (закон двойного отрицания):  . .2. Коммутативность 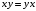 , ,  . .3. Ассоциативность  , ,  . .4. Дистрибутивность (распределительные законы)  , ,  . .5. Законы поглощение 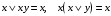 . .6. Законы де-Моргана 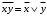 , , 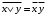 . .7. Правило Блейка  Упражнения. Доказать эти свойства. Определение. Булевой алгеброй называется непустое множество M с тремя операциями & (аналог конъюнкции), 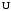 (аналог дизъюнкции) и (аналог дизъюнкции) и  (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых элементов (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых элементов  , ,  и и  из множества M из множества Mверны перечисленные выше свойства (аксиомы). Такие алгебры ввёл и изучал Джордж Буль – английский математик середины 19 века, заложивший основы математической логики. Таким же аксиомам удовлетворяют операции пересечения, объединения и дополнения в теории множеств и, соответственно, операции в алгебре событий в теории вероятностей. Это всё булевы алгебры. Конечно, в перечисленных свойствах (аксиомах) некоторые аксиомы вытекают из других, не используя таблицы истинности. Выделением минимального числа аксиом мы заниматься не будем (оставим это дело математикам). Упражнения. Докажите соотношения, не используя таблицы истинности. 1.  . .2.  . .3.  . .§2. Логические (булевы) функции Как было определено в §1 логическая функция 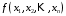 и все её логические переменные принимают только два значения 0 и 1. Таким образом логическая функция от и все её логические переменные принимают только два значения 0 и 1. Таким образом логическая функция от  переменных определена на множестве упорядоченных наборов длины переменных определена на множестве упорядоченных наборов длины  , состоящих из нулей и единиц. , состоящих из нулей и единиц. Отметим, что упорядоченный набор значений переменных, состоящий из нулей и единиц, есть размещение с повторениями (см. начало курса теории вероятностей) 2-ух элементов  по по  местам. Число таких размещений равно местам. Число таких размещений равно 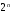 . С геометрической точки зрения эти упорядоченные наборы можно трактовать как координаты вершин единичного куба в пространстве . С геометрической точки зрения эти упорядоченные наборы можно трактовать как координаты вершин единичного куба в пространстве  . .Лемма. Число логических функций от  переменных равно переменных равно  . .Доказательство. Область определения функции состоит из 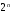 точек. В каждой точке функция принимает одно из двух значений: либо 0 либо 1. Таким образом, логическая функция от точек. В каждой точке функция принимает одно из двух значений: либо 0 либо 1. Таким образом, логическая функция от  переменных – размещение с повторениями объёма переменных – размещение с повторениями объёма 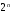 из двух элементов из двух элементов  . Таких различных функций (размещений) равно . Таких различных функций (размещений) равно  . .Для того чтобы сравнить различные логические функции надо сначала упорядочить точки области определения. Воспользуемся методом (способом) “скользящей единицы”. В этом методе упорядоченный набор нулей и единиц трактуют как число, записанное в двоичной системе. Тогда, стартуя от последовательности нулей прибавляю единицу в двоичной системе получим все наборы переменных. Пример. Записываем в столбец результаты метода. Пусть  . Тогда . Тогда
Пусть 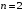 . Тогда . Тогда
Пусть 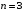 . Тогда . Тогда
Теперь можем выписать таблицы истинности для любых функций, присоединяя справа к таблице аргументов столбец значений функции при соответствующих значениях аргументов. Для того чтобы выписать все функции воспользоваться методом “скользящей единицы”. Найдём все функции одной переменной (  ). Тогда число логических функций равно 4. Составим заготовку таблицы для четырёх функций одной переменной ). Тогда число логических функций равно 4. Составим заготовку таблицы для четырёх функций одной переменной
Далее, заполним две нижние строки методом “скользящей единицы”.
Здесь запись двоичного числа производится в столбец, причём младшие разряды ниже старших. Теперь узнаём и обозначаем найденные функции:  – постоянная функция (логическая константа 0); – постоянная функция (логическая константа 0); – тождественная функция; – тождественная функция; – функция отрицания; – функция отрицания; – постоянная функция (логическая константа 1). – постоянная функция (логическая константа 1).Найдём все функции двух переменных ( 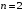 ). Тогда число логических функций равно 16. По тем же правилам, что и для функций одной переменной составим таблицы истинности для этих шестнадцати функций. ). Тогда число логических функций равно 16. По тем же правилам, что и для функций одной переменной составим таблицы истинности для этих шестнадцати функций.
В этой таблице некоторые функции нам уже известны (они указаны в нижней строке). Выделим часто встречающиеся функции, их обозначения и названия:  – штрих Шеффера; – штрих Шеффера; – стрелка Пирса; – стрелка Пирса; – сложение по модулю 2. – сложение по модулю 2.Оставшиеся две функции 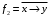 и и  встречаются редко. встречаются редко.Упражнения. Убедится в справедливости равенств 1. 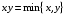 , , 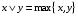 . .2. 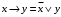 , ,  , , 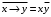 , ,  . .3.  . .4.  . .5. 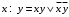 . .6. 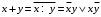 . . |