Элементы математической статистики и корреляционного анализа. Индивидуальные задания разбиты на три уровня сложности. Представлены примеры решения наиболее сложных задач

• Название: Элементы математической статистики и корреляционного анализа. Индивидуальные задания разбиты на три уровня сложности. Представлены примеры решения наиболее сложных задач
• Дата: 16.04.2022
• Размер: 326 Kb.
• Имя файла: M-20 (1).doc
• Тип: Реферат; #477682
• страница: 5 из 5

2.6. Задание 6
Для двух случайных величин X и Y проведена серия испытаний. Результаты испытаний записаны в следующую корреляционную таблицу:

Таблица 2.4

Индивидуальные данные к заданию 6

Х Y	0	1	2	3	4	5
1		C
2	D		B
3			1	2	A	1
4					1

1. 
   Вычислить выборочные характеристики MX, MY, исправленные SX, SY, коэффициент корреляции _XY.
   
2. 
   Проверить для доверительной вероятности  = 0,95 значимость коэффициента корреляции _XY.
   
3. 
   Написать уравнения прямых регрессий Y на X и X на Y.
   
4. 
   В подходящем масштабе изобразить на графике точки (x, y) из корреляционной таблицы и прямые регрессии.
   

7. 
   Задание 7
   

Над случайными величинами X, Y, Z проведена серия из 8 наблюдений. Результаты записаны в таблицу

Таблица 2.5

Индивидуальные данные к заданию 7

	X	Y	Z
1	1	A	0
2	0	1	A
3	2	B	3
4	C	2	3
5	3	1	1
6	2	0	-1
7	A	3	B
8	1	C	D

Вычислить:

1. 
   матрицу моментов;
   
2. 
   корреляционную матрицу;
   
3. 
   коэффициент множественной корреляции между переменной Z (как функции от X, Y) и переменными X, Y.
   

3. Примеры решения задач
Пусть N = 9, n = 50. Тогда А = 12, В = 3, С = 2, D = 3.

1. 
   Пример 1
   

Рассмотрим пример решения задачи 6.

Для заданных значений параметров А, В, С, D корреляционная таблица имеет вид:

Таблица 3.1

Корреляционная таблица для заданных А, В, С, D.

X Y	0	1	2	3	4	5
1		3				
2	3		2			
3			1	2	12	1
4					1	

Объём выборки равен 2 +3 + 3 +1 + 2 + 12 + 1 + 1 = 25.

1. 
   Вычислим выборочные характеристики:
   

M[X] = = ;

M[Y] = = ;

;

;

;

;

S[X] = 1,532; S[Y]= 0,748;

cov(X, Y) = M[XY] – M[X]M[Y]= ;

0,796.

2)Пусть гипотеза H₀ такова: коэффициент корреляции значим. Конкурирующая гипотеза H₁: коэффициент корреляции не значим. Для проверки гипотезы H₀ необходимо найти arcthR(X, Y) и , где n – объём выборки (n = 25), t(P) – квантиль нормального распределения, который находится из условия 2Ф(t) = P, где Ф(t) – функция Лапласа, P – доверительная вероятность. Если |arcthR(X,Y)| > , то с доверительной вероятностью P гипотеза H₀ принимается, в противном случае – принимается конкурирующая гипотеза.

Пусть гипотеза H₀ такова: коэффициент корреляции R(X, Y) близок к единице. Конкурирующая гипотеза H₁: коэффициент корреляции далек от единицы. Вычислим . Если arcth|R(X,Y)| > , то с доверительной вероятностью P гипотеза H₀ принимается, в противном случае принимается гипотеза H₁.

Найдем

arcthR(X,Y) = arcth 0,796 = 1,088.

Пусть доверительная вероятность P равна 0,95. Тогда 2Ф(t) = 0,95. Ф(t) = 0,475. По таблице значений функции Лапласа находим t = 1,96.

= =0,418. 1,088>0,418, следовательно, коэффициент корреляции в нашем случае считается значимым.

0,446. 1,088 > 0,446, следовательно, коэффициент корреляции близок к единице.

3)В общем случае уравнения прямых регрессий имеют вид:

Y на X: ,

X на Y: .

При решении данной задачи уравнения прямых регрессий примут вид:

y – 2,6 = 0,388(x – 2,88);

x – 2,88 = 1,63(y – 2,6).

Графически прямые регрессии изображены на рис. 3.1.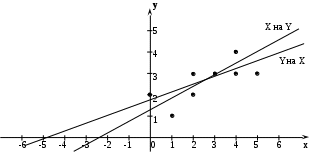




Рис. 3.1. Прямые регрессии

2. 
   Пример 2
   

Рассмотрим пример решения задачи 7.

При заданных значениях параметров выборка для X, Y и Z имеет вид:

Таблица 3.2

Выборка для X,Y и Z

№	1	2	3	4	5	6	7	8
X	1	0	2	3	3	2	12	1
Y	12	1	2	2	1	0	3	3
Z	0	12	3	3	1	-1	2	3

1. 
   Вычислим матрицу моментов. Объём выборки равен 8.
   

Найдем 3; 3; .

21,5; 21,5;

.

D[X] = M[X²] – M²[X]=12,5; аналогично, D[Y] = 12,5; D[Z] = 13,859.

= 3,536; S[Y] = 3,536; S[Z] = 3,723.

;

;

.

cov(X,Y)=8-33= -1; cov(X,Z) = cov(Y,Z) =

Матрица моментов запишется в виде: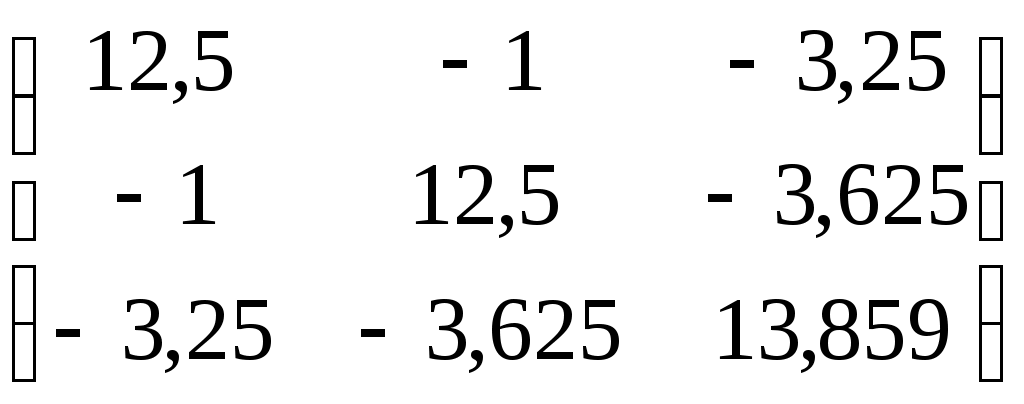

.

2)Вычислим коэффициенты корреляции.

; ;

.

Запишем корреляционную матрицу.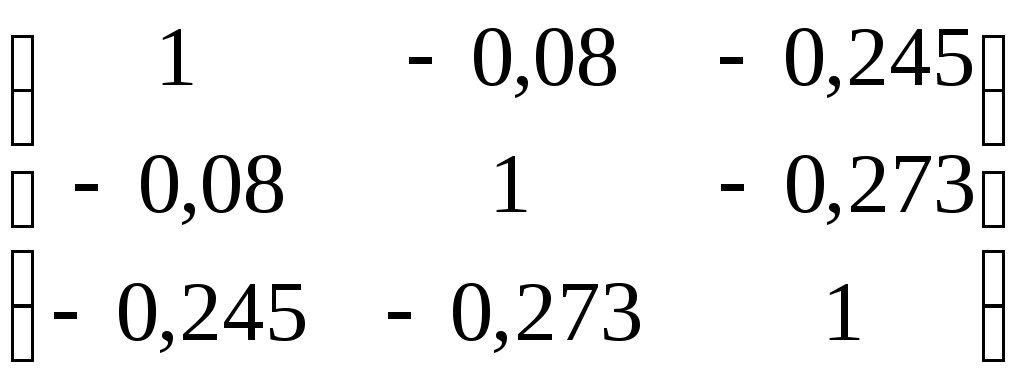

.

3)Коэффициент множественной корреляции вычисляют по формуле:



В нашем случае R(Z,XY) =0,383.

Библиографический список

1. 
   Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения. М.: 1986.
   
2. 
   Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высш. шк., 1997.
   
3. 
   Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. шк., 1997.
   
4. 
   Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. М.: Наука, 1978.