Энтропия. Энтропия

• Название: Энтропия. Энтропия
• Дата: 05.09.2022
• Размер: 114.5 Kb.
• Имя файла: 1881_entropiya.doc
• Тип: Документы; #663597

www.testent.ru

ЭНТРОПИЯ.
Энтропия – это мера беспорядка.
Р

1 _а произвольный обратимый

Цикл

Разобьем его близкими адиабатами на

_d циклы Карно.

2 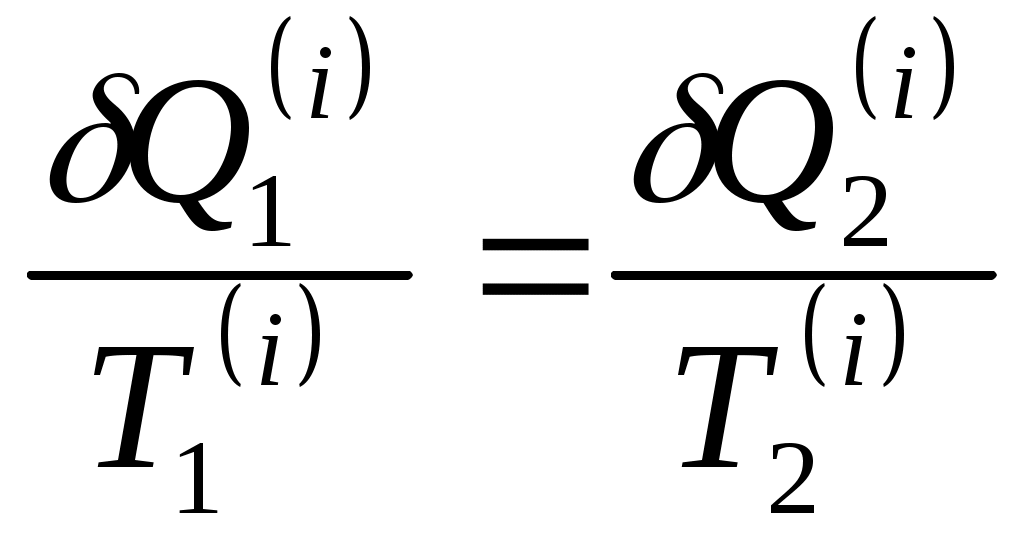учитывая, что

V мы переносим все влево:

произвольный обратимый

цикл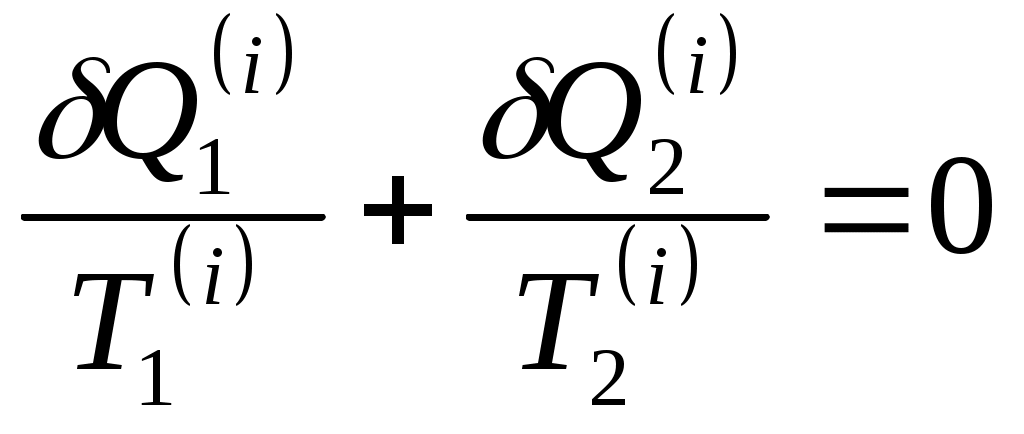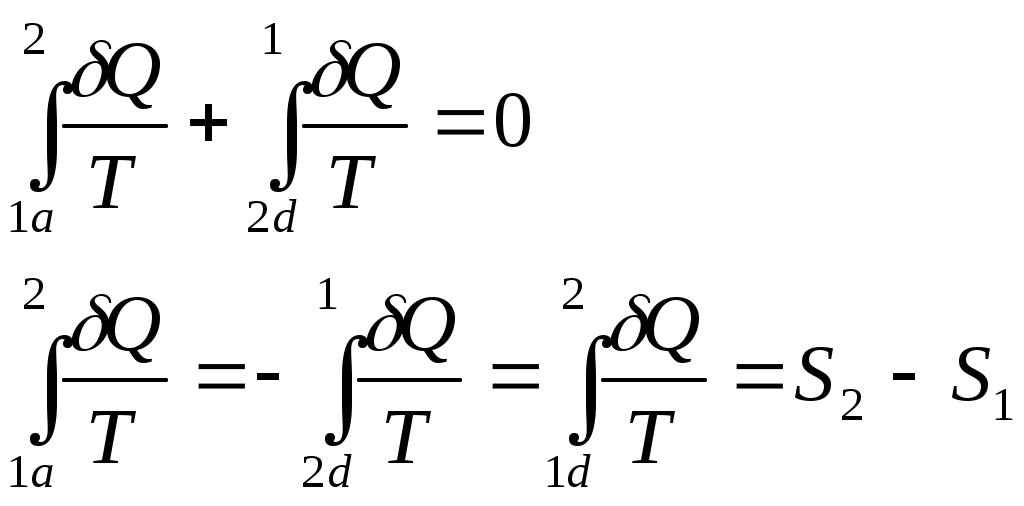



(1)


Интеграл не зависит от того, переводим мы систему из состояния 1 в состояние 2 по верхней ветке или по нижней.

Интеграл не зависит от пути перехода, он определяется разностью состояний
S (энтропия) – однозначная функция состояния термодинамической системы. Изменение энтропии характеризует направление протекания процессa.

(1)
Если система изолированная, т.е. , то энтропия сохраняется. Например, при адиабатическом процессе энтропия сохраняется, это называется изэнтропа.


Т

1. 
   2
   

Цикл Карно

4. 
   3
   

S
Оказалось, что этот интеграл не зависит от пути перехода из состояния 1 в 2, поэтому можно описывать состояние 1 параметром S₁, состояние 2 параметром S₂ (для обратимых процессов).

Теперь рассмотрим необратимый процесс:
Р Дополним его обратимым процессом

_а и разобьем близкими адиабатами

¹

_{d 2}



V

Если система изолированная, т.е. , то

Вторая формулировка второго начала термодинамики: все реально протекающие процессы в изолированной (замкнутой) системе идут с возрастанием энтропии. Все процессы идут до тех пор, пока энтропия достигнет максимума. Максимум энтропии – равновесное состояние системы.

Задача 1:

Есть 1 моль идеального газа, с ним происходят процессы. Как измениться энтропия? (об изоляции речь не идет)
Решение: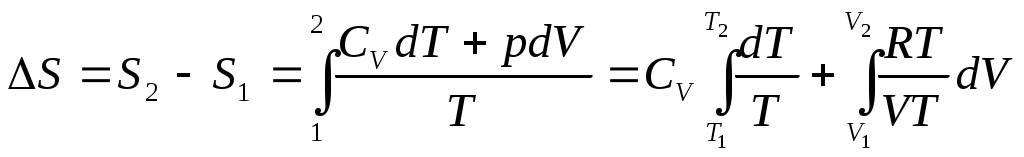



: =>
- случай, когда меняется температура и объем.

Если процесс изотермический, то останется только второе слагаемое, если изохорический - останется только первое слагаемое.
Задача 2:

Есть 2кг льда при температуре -10˚С. Как измениться энтропия, если этот лед превратить в пар при температуре 100˚С?
Решение:

Лед нагревали, он плавился, нагревали воду, происходило испарение.

- удельная теплота плавления.

- удельная теплота парообразования- количество тепла, необходимое для испарения единицы массы.

- теплоемкость льда.

- теплоемкость воды.





для каждого процесса свое изменение энтропии

Нагревание льда: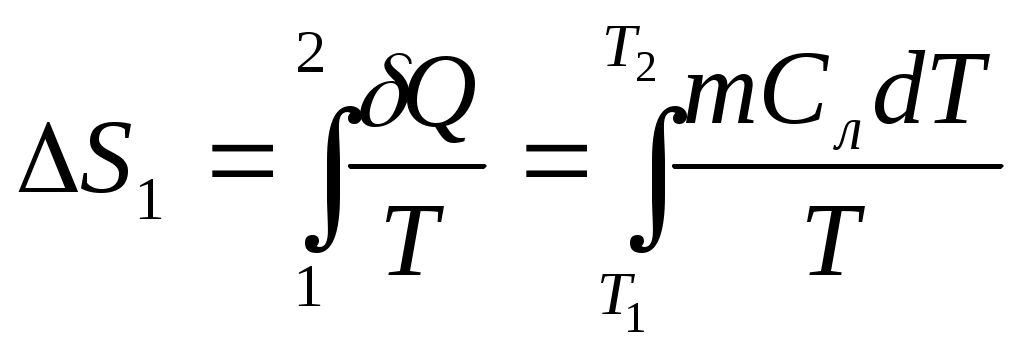



Плавление льда:



Нагревание воды: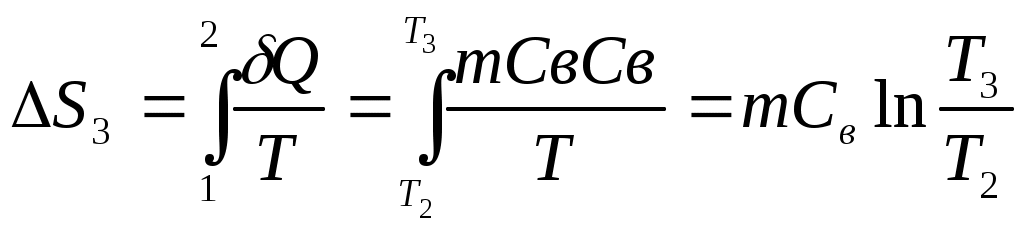



Испарение:

.








Статистический смысл Второго начала термодинамики:

(2)- формула, написанная на памятнике Больцмана.

(2) – определение энтропии с помощью статистики, т.е. чем разупорядоченнее система, тем больше энтропия, ведь энтропия мера беспорядка.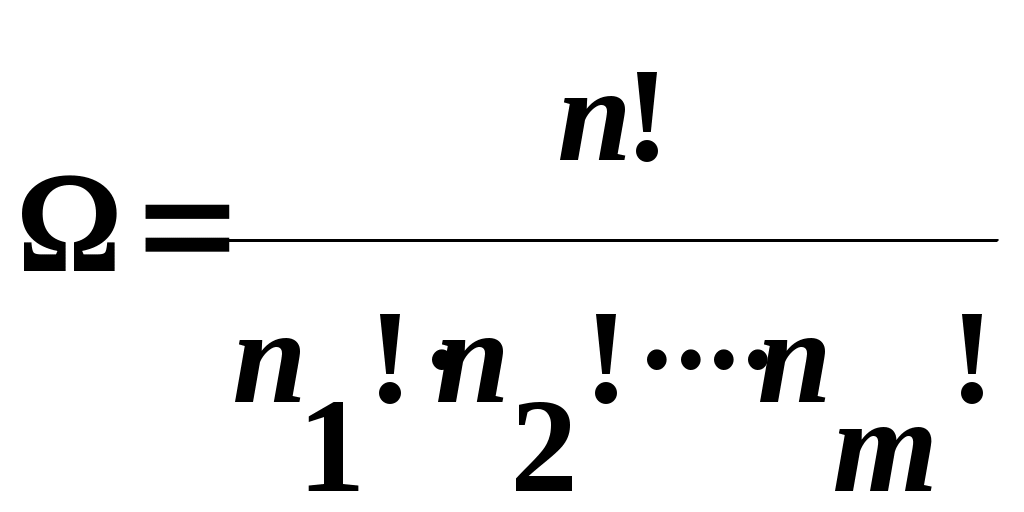

- термодинамическая вероятность – число способов (микросостояний), которыми можно осуществить рассматриваемое макросостояние:

n – полное число частиц

n_i- число частиц, находящихся в i-ом состоянии.

- самое неупорядоченное состояние




- упорядоченное состояние